2019年大学入試センター数学ⅠA第1問[２]（集合と命題）（配点10点）問題・解答・解説

解答（計10点）　シ（2点）　ス（2点）セ（2点）ソ（2点）タ（2点）

解説

シス

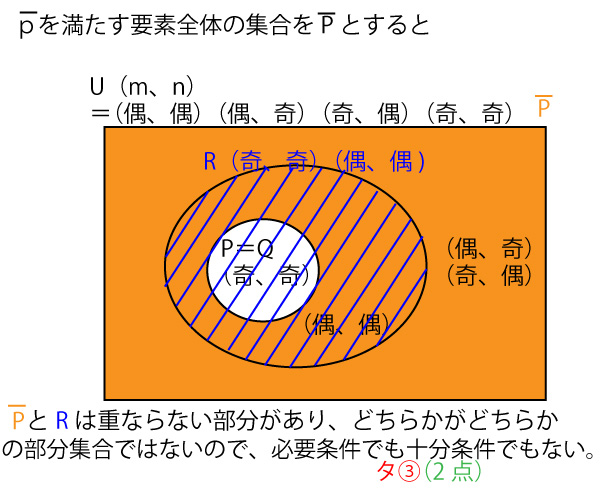
ｐが（m、n)＝（奇数、奇数）なので、は（m、n)＝（偶数、偶数）（偶数、奇数）（奇数、偶数）。
するとｍが奇数ならば、ｎは偶数。シ（2点）
ｍが偶数の場合は、nは偶数でも奇数でもよい。ス（2点）

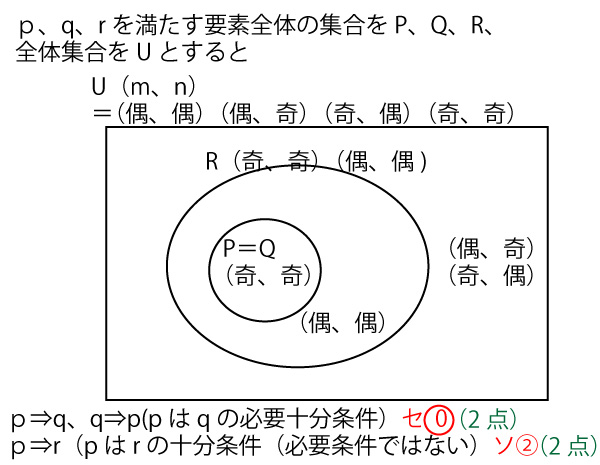
セソタ

ｐ：（ｍ、ｎ）＝（奇数、奇数）
q：（m、ｎ）＝（奇数、奇数）
（どちらかでも偶数であると3mnは偶数になってしまう）
ｒの条件を考えると
・（m、n)＝（偶数、偶数）のとき、m+5n＝偶数＋偶数＝偶数
・（m、n)＝（偶数、奇数）のとき、m+5n＝偶数＋５×奇数＝偶数＋奇数＝奇数
・（m、n)＝（奇数、偶数）のとき、m+5n＝奇数＋偶数＝奇数
・（m、n)＝（奇数、奇数）のとき、ｍ＋5n＝奇数＋５×奇数＝奇数＋奇数＝偶数
つまり
ｒ：（ｍ、ｎ）＝（偶数、偶数）か（奇数、奇数）

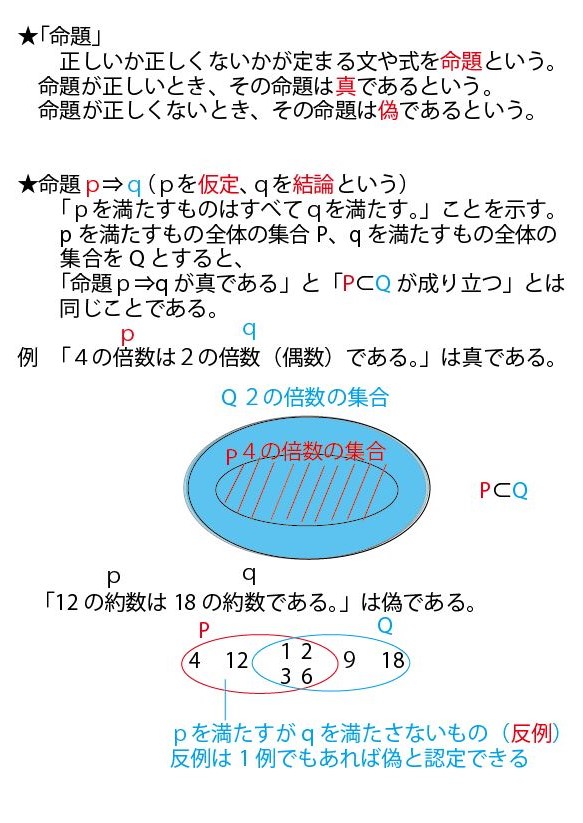
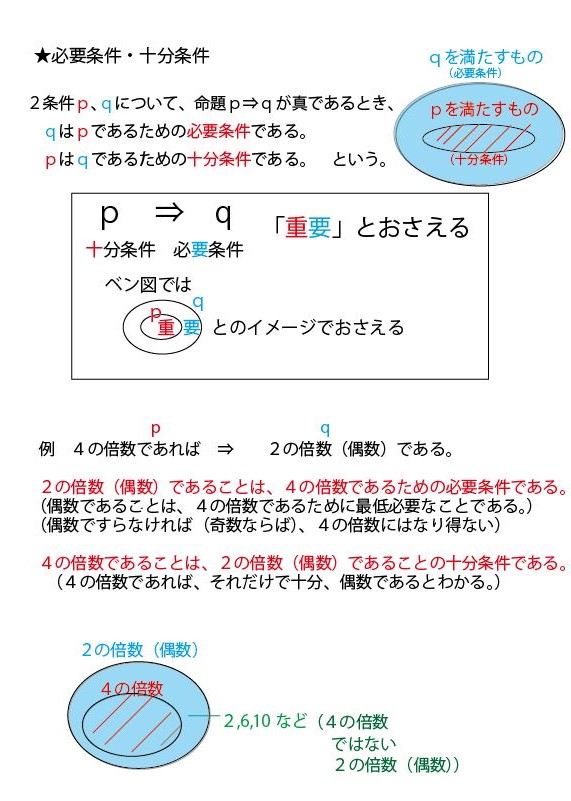
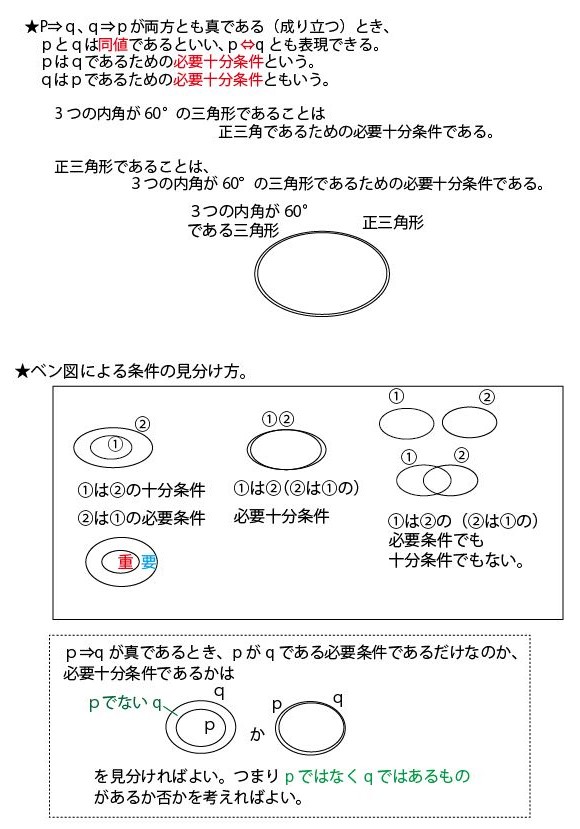
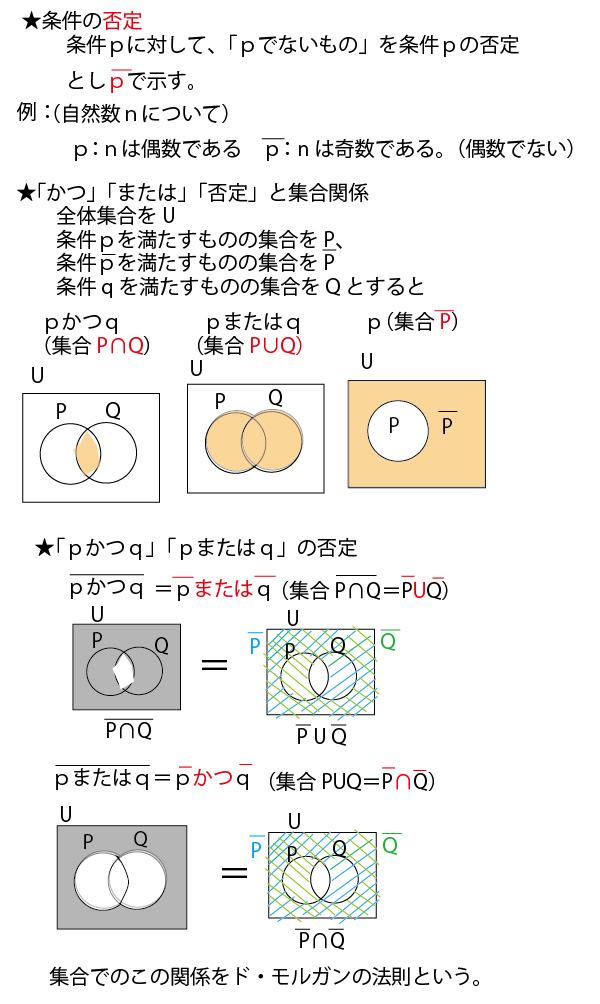
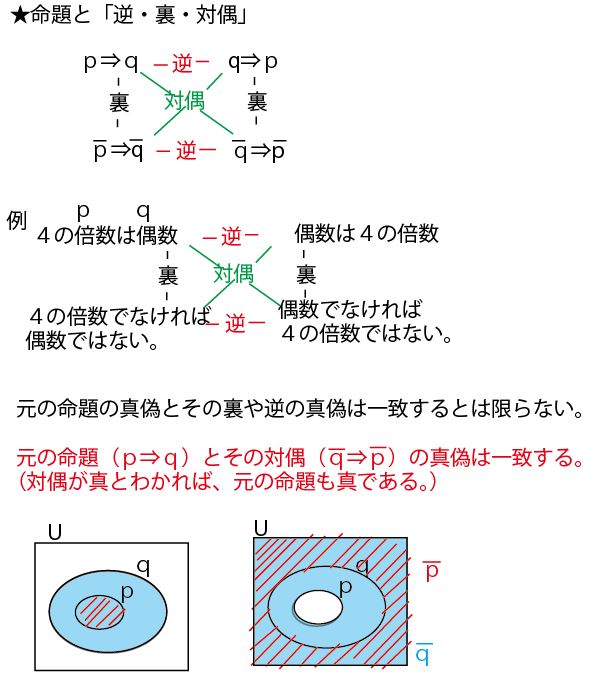
集合と命題の基礎知識の整理

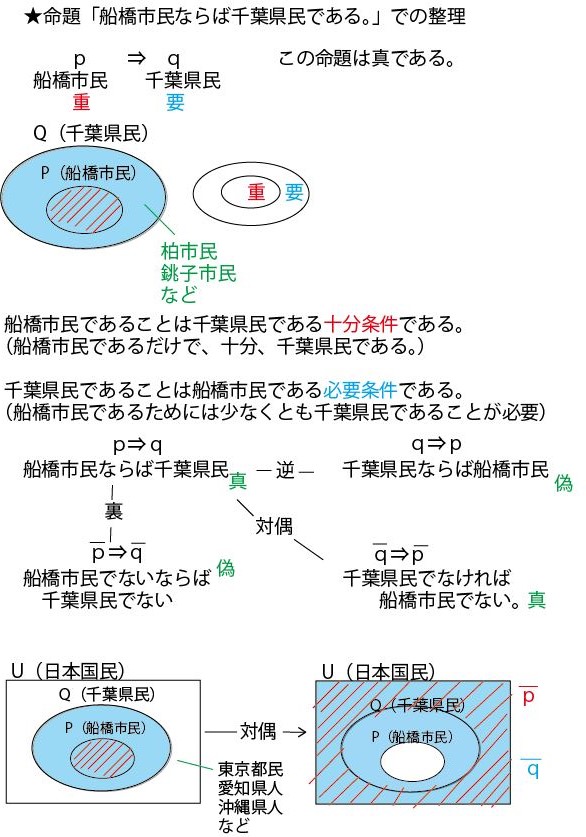
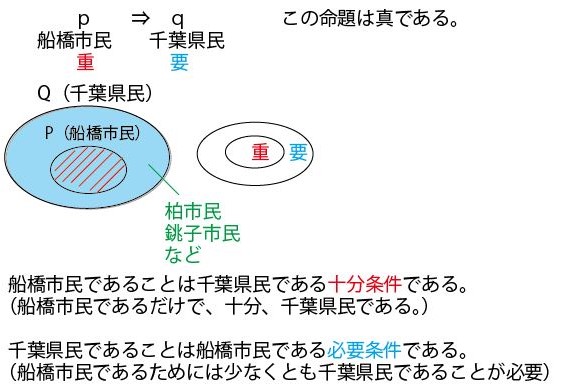
以上の解説で理解できる方はそれで大丈夫です。ただ、理解が不十分な方は、以下で「命題と集合」に関する考え方、特にベン図での捉え方を整理しますので、お読みください。前半は「4の倍数は２の倍数」を例に数学的に説明します。ただそれだけでは、イメージや理解が不十分の方のために最後に日本語的なたとえ「船橋市民は千葉県民である」で補足説明していますので合わせてご覧ください。