2022年6月 予備校講師・船橋市議(無党派) 朝倉幹晴
大学入試センター試験2020年数学ⅡB第1問[1](三角関数、計15点)の解答、解説を作成しました。学習、入試対策にご活用ください。
(1)0≦θ<2π(パイ)のとき
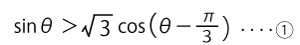
となるθの値の範囲を求めよう。
加法定理を用いると

である。よって、三角関数の合成を用いると、 は
は

と変形できる。したがって、求める範囲は

である。
(2)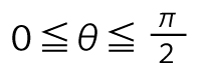 とし、kを実数とする。sinθとcosθはxの2次方程式25x2−35x+k=0の解であるとする。
とし、kを実数とする。sinθとcosθはxの2次方程式25x2−35x+k=0の解であるとする。
このとき、解と係数の関係によりsinθ+cosθとsinθcosθの値を考えれば、
k=ケコ(2点)であることがわかる。
さらに、θがsinθ≥cosθを満たすとすると、
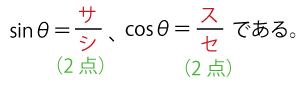
このとき、θはソ(2点)を満たす。ソに当てはまるものを、次ののうちから一つ選べ。
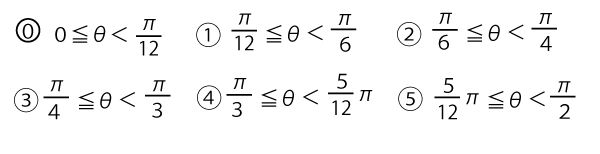
[next_p]