2023年大学入試共通テスト「数ⅡB」第2問[1](配点15点)問題・解答・解説
2024年1月9日 予備校講師・船橋市議 朝倉幹晴
2023年大学入試共通テスト「数学2B」第2問[1](配点15点)の解答・解説を作成しましたので、ご活用ください。問題文の最後の所でページ番号「2」をクリックすると解答・解説に飛びます。
ⅡBの解答解説は順次作成中ですが、IAは完成していますのでご活用ください。
2023年数学ⅡB第1問[1](配点18点)問題・解答・解説
2023年大学入試共通テスト「数ⅡB」第1問[2](配点12点)問題・解答・解説
2023年大学入試共通テスト「数学ⅡB」第2問[1](配点15点)
[1](1)kを正の定数とし、次の3次関数を考える。
f(x)=x2(k-x)
y=f(x)のグラフとx軸との共有点の座標は(0,0)と(ア,0)(1点)である。
f(x)の導関数f´(x)は
f´(x) =イウx2+エkx(イウエ合わせて4点)
である。
x=オ(1点)のとき、f(x)は極小値カ(1点)をとる。
x=キ(1点)のとき、f(x)は極大値ク(1点)をとる。
また、0<x<kの範囲においてx=キのときf(x)は最大となることがわかる。

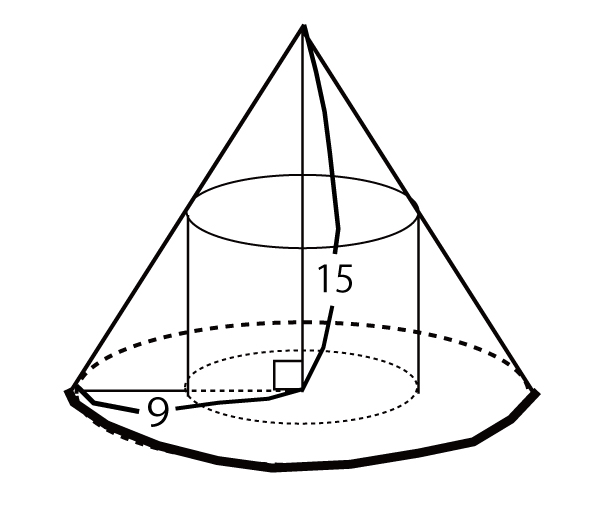
(2)右の図のように底面が半径9の円で高さが15の円錐に内接する円柱を考える。円柱の底面の半径と体積をそれぞれx、Vとする。Vをxの式で表すと
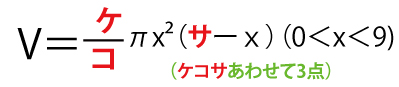
である。(1)の考察より、x=シのときVは最大となることがわかる。Vの最大値はスセソπとなる。