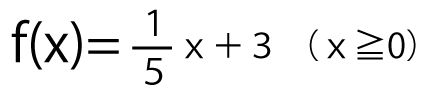2023年大学入試共通テスト「数ⅡB」第2問[2](配点15点)問題・解答・解説
2024年1月9日 予備校講師・船橋市議 朝倉幹晴
2023年大学入試共通テスト「数学2B」第2問[2](配点15点)の解答・解説を作成しましたので、ご活用ください。問題文の最後の所でページ番号「2」をクリックすると解答・解説に飛びます。
ⅡBの解答解説は順次作成中ですが、IAは完成していますのでご活用ください。
2023年数学ⅡB第1問[1](配点18点)問題・解答・解説
2023年大学入試共通テスト「数ⅡB」第1問[2](配点12点)問題・解答・解説
2023年大学入試共通テスト「数ⅡB」第2問[1](配点15点)問題・解答・解説
2023年大学入試共通テスト「数学ⅡB」第2問[2](配点15点)
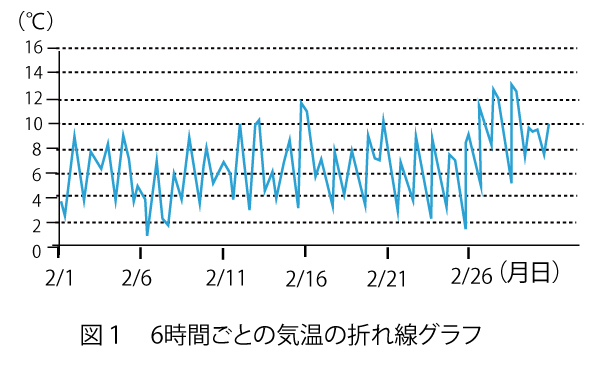
(2)ある地域では、毎年3月頃「ソメイヨシノ(桜の種類)の開花予想日」が話題になる。太郎さんと花子さんは、開花日時を予想する方法の一つに、2月に入ってからの気温を時間の関数とみて、その関数を積分した値をもとにする方法があることを知った。ソメイヨシノの開花日時を予想するために、二人の図1の6時間ごとの気温の折れ線グラフを見ながら、次のように考えることにした。
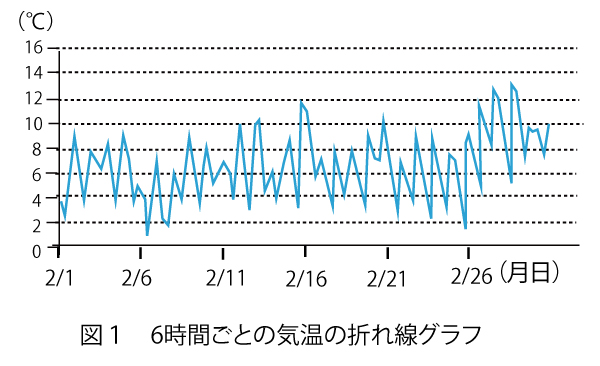
xの値の範囲を0以上の実数全体として、2月1日午前0時から24x時間経った時点をx日後とする。(例えば、10.3日後は2月22日午前7時12分を表す。)また、x日後の気温をy℃とする。このとき、yはxの関数であり、これをy=f(x)とおく。ただし、yは負にならないものとする。気温を表す関数f(x)を用いて二人はソメイヨシノの開花日時を次の設定で考えることにした。
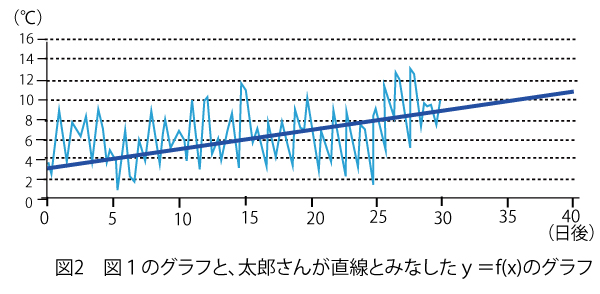
設定のもと、太郎さんは気温を表す関数y=f(x)のグラフを図2のように直線とみなしてソメイヨシノの開花日時を考えることにした。
として考えた。このとき、ソメイヨシノの開花日時は2月に入ってからノとなる。
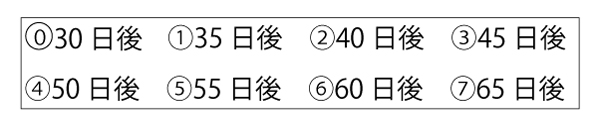
(ⅱ)太郎さんと花子さんは、2月に入ってから30日後以降の気温について話をしている。
太郎:1次関数を用いてソメイヨシノの開花日時を求めてみたよ。
花子:気温の上がり方から考えて、2月に入ってから30日後以降の気温を表す関数が2次関数の場合も考えてみようか。


[next_p]