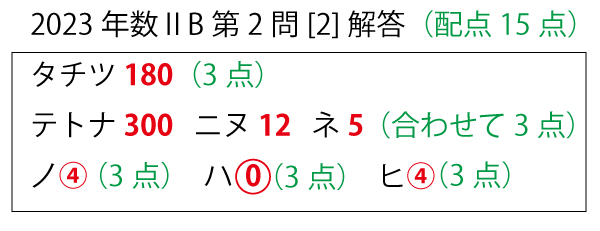
2023年大学入試共通テスト「数ⅡＢ」第2問[2]（配点15点）問題・解答・解説

解説



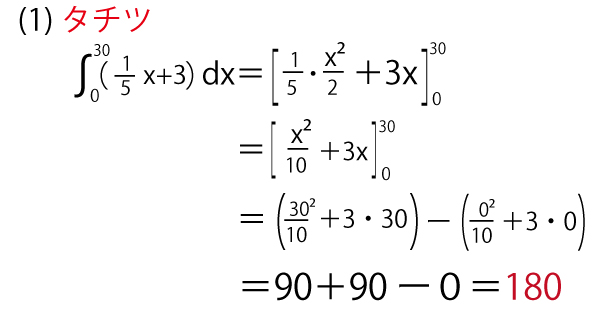
ハ
「ｘ≧30の範囲でf(x)は増加すること」となること、f(x)が2月以降は正の値であることと、定積分の面積的な定義を考えてみると、ハは以下の図のように説明できる。

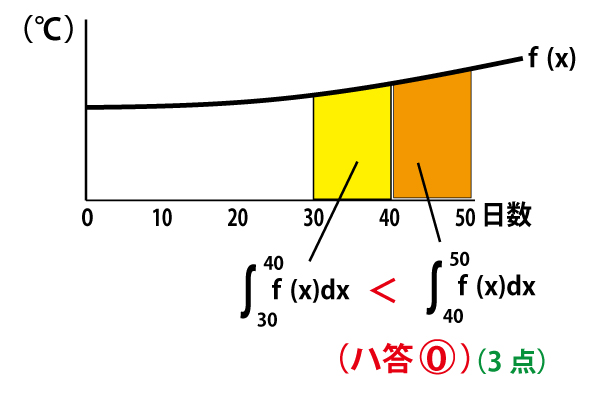
図から明らかであるが、更に以下のようにも説明できる。
左側の黄色い面積と右側のオレンジの面積を比較する。それぞれの30～40、40～50のf(x)の値の平均値を考え、その平均値を上の辺とする長方形に黄色とオレンジの面積を置き換える。２つの長方形の横の長さは10で同じである。一方、縦の長さ（高さ）は30～40区間＜40～50区間となるので、オレンジの長方形の面積のほうが大きい。

ヒ

本文より、f(x)を１次関数で定義したときと2次関数で定義した時で、30日では一致するので、０～30日は計算が楽なほうの1次関数で最初に求めた値180で考える。次の花子さんの「30日後以降の気温を表す関数が2次関数の場合も考えてみようか。」にしたがって、30～40日は2次関数で考えて、115の値が出る。
すると合わせて、0～40日では、180＋115＝295となる。
ハで議論したように、40～50の範囲は30～40の範囲の115より大きくなるはずなので、115＋α（α＞0）となる。
すると
０～50日では、295＋115＋α＝410＋α＞400

すると40日目では295で未開花であるが、50日目には410＋αで開花済である。
よって、40日後より後、50日後より前（）（3点）

【大学入試共通テストにおける出題の傾向】
！A第２問［２］（バスケットボールコートへのシュート）もⅡB第2問［２］（ソメイヨシノの開花時期）も、共に現実社会や日常生活の中の出来事を数学の目で分析しようとする興味深い問題である。
2023年大学入試共通テスト「数学１A」第2問［２］（15点）問題・解答・解説

そして一見複雑そうな式がでてくる（本設問では2次関数の積分）。しかし、その式の深い解釈・非常に難しい計算までは求められず、「考え方」のほうが聞かれている。あせらず、問題の指示を読み、その指示された内容を考えていくとできるので難しそうな式にビビらない（「聞かれているのはそんなに難しいはすはない」と考え直す）ことが大切である。