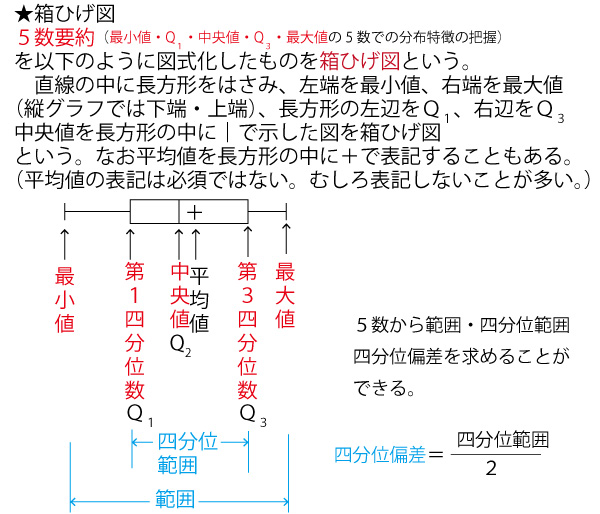
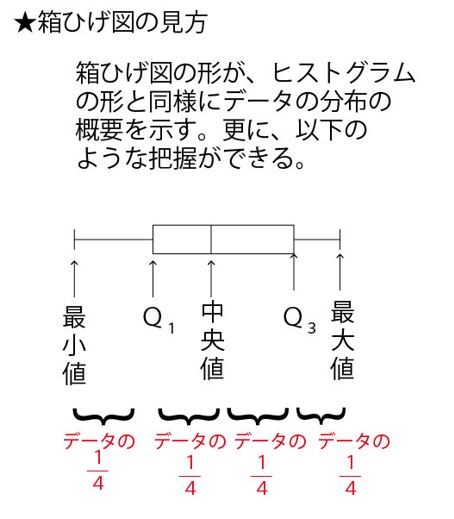
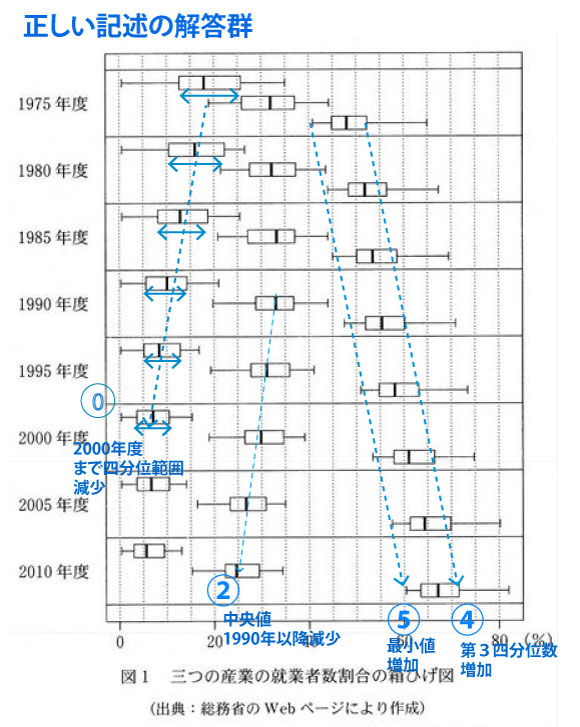
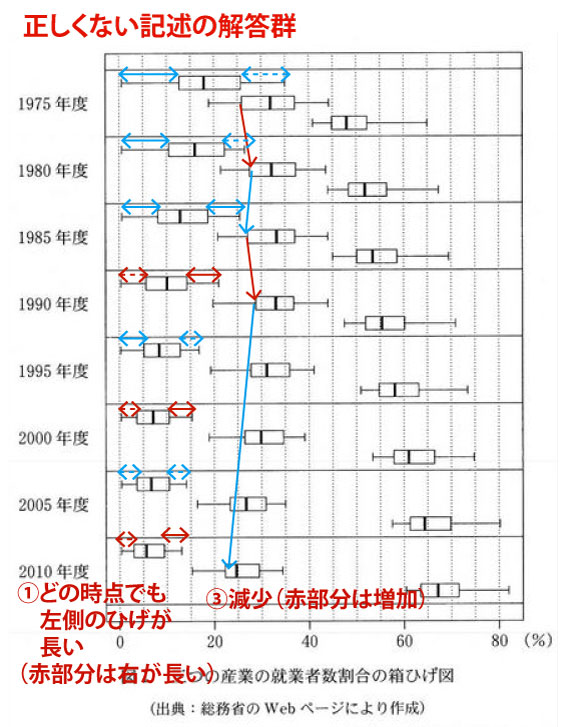
2021年大学入試共通テスト「数学IA」第2問[2](統計)問題・解答・解説配点15点)
(1)タ・チについて。
設問は、「正しい選択肢」を選ぶのではなく、「正しくない選択肢」を選ぶ問題であるので間違えないこと。試験の時は「正しくない」という部分に下線を引いて間違えないように留意するとよい。
1点でも正しくない例(反例)があれば「正しくない」。
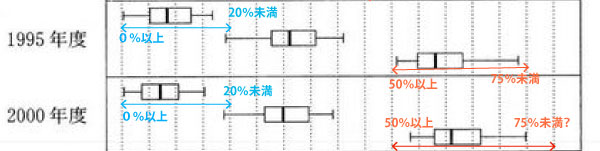
(![]() に関しては、1985年度・1995年度・2005年度は、左のひげと右のひげが同じ長さにも、少し右のひげが長いようにも見えるので判断に迷う。しかし1990年度・2000年度・2010年度は明確に右のほうが長いので、正しくない記述とわかる)。
に関しては、1985年度・1995年度・2005年度は、左のひげと右のひげが同じ長さにも、少し右のひげが長いようにも見えるので判断に迷う。しかし1990年度・2000年度・2010年度は明確に右のほうが長いので、正しくない記述とわかる)。
よってタ・チの答は![]() と
と![]()
(各2点計4点、回答の順序は問わない)
(2)ツ・テについて
問題文に「ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。」とある。左側は各階級の範囲の最小値で、右側は最大値側である。この問題だけに限らず、度数分布表やヒストグラムの各階級は「△△以上~〇〇未満」という形で設定されていることがほとんどである。(階級を「△△より大きい~〇〇以下」という形で設定することも不可能ではない。)
ヒストグラムと対応する箱ひげ図の最大値・最小値がちょうど階級間の境界と一致した場合は、「△△以上~〇〇未満」の階級に含まれることになることに注意してほしい。
本設問で箱ひげ図の最小値・最大値が階級の境界にある場合の例(1975年度第3次産業、1985年第3次産業)で考えてみよう。
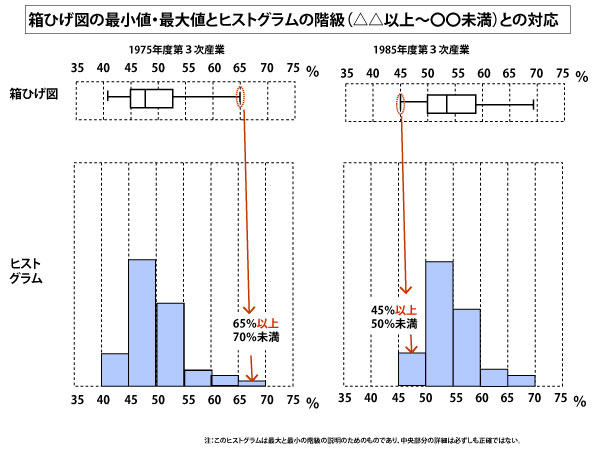
その点に注意した上で、箱ひげ図、ヒストグラムで値が存在する全体の範囲を「〇〇以上、△△未満」で確かめてみて、まず一致するものを選ぶ。その上で、一致するものが複数ある場合は、ヒストグラムの形と箱ひげ図の第1四分位数・中央値・第3四分位数が一致するものを選ぶ。
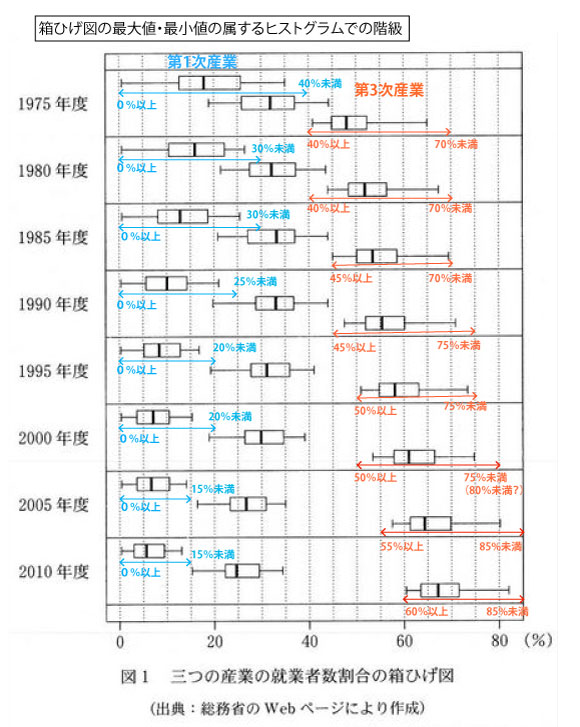
2000年度の最大値は、75%より小さいのか、75%の線上なのかどちらにも読み取れるので、75%未満とともに( )で75%の線上と考えた場合の「(80%未満?)」も併記した。
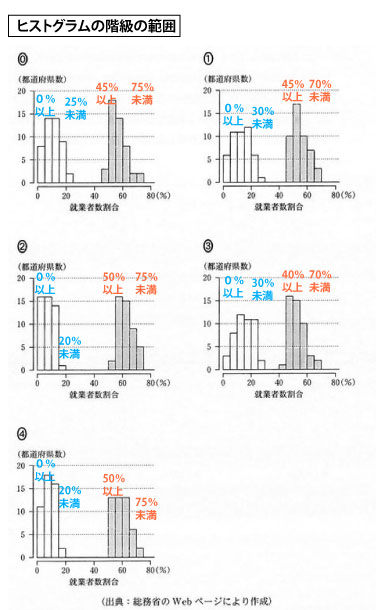
すると以下は1対1で対応し、選ぶことができる。
1975年度 箱ひげ図では第1次産業の最大値が40%未満である。そのヒストグラムは存在しない。
1980年度![]() (第1次産業0%以上30%未満。第3次産業40%以上70%未満)
(第1次産業0%以上30%未満。第3次産業40%以上70%未満)
1985年度![]() (第1次産業0%以上30%未満。第3次産業45%以上70%未満)
(第1次産業0%以上30%未満。第3次産業45%以上70%未満)
(ツ)(2点)
1990年度![]() (第1次産業0%以上25%未満。第3次産業45%以上75%未満)
(第1次産業0%以上25%未満。第3次産業45%以上75%未満)
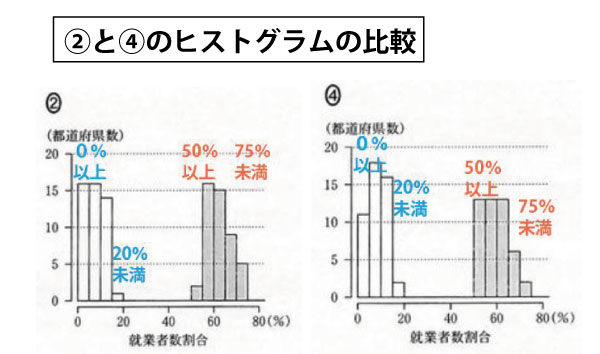
1995年度 ![]() か
か![]()
(第1次産業0%以上20%未満。第3次産業50%以上75%未満)
2000年度 ![]() か
か![]()
(第1次産業0%以上20%未満。第3次産業50%以上75%未満)
(2000年度の箱ひげ図の最大値を75%未満と解釈した場合)
2005年度・2010年度 第1次産業の箱ひげ図の最大値は15%未満であるが、そのヒストグラムは存在しない。
問題文に「8時点の中から5時点を取り出して考える。各時点における都道府県別の、第1次産業と第3次産業の就業者数割合のヒストグラムを一つのグラフにまとめてかいたものが、以下の五つのグラフである。」
とある。つまり五つのヒストグラムともどこかの年度のものなので、2000年度の箱ひげ図の最大値を80%未満と解釈してしまうと、 ![]() か
か![]() のどちらかが該当年度がなくなってしまい問題の設定と矛盾する。したがって、本設問では2000年度の最大値を75%未満と解釈していると読み取ることができる。
のどちらかが該当年度がなくなってしまい問題の設定と矛盾する。したがって、本設問では2000年度の最大値を75%未満と解釈していると読み取ることができる。
したがって、1995年度と2000年度は、第1次産業・第3次産業ともに同じ最大値・最小値となるので、その情報だけでは、それぞれが![]() か
か![]() のどちらかは判断できない。
のどちらかは判断できない。
したがって、箱ひげ図の他の情報(第1四分位数・中央値・第3四分位数)から、該当するヒストグラムを選ぶ。
第1次産業に関しては、![]() のほうが小さい値の都道府県が多く、第1四分位数が最小値寄り(箱ひげ図で左のひげが短い)であるはずである。
のほうが小さい値の都道府県が多く、第1四分位数が最小値寄り(箱ひげ図で左のひげが短い)であるはずである。
第3次産業に関しては、![]() のほうが小さい値の都道府県が多く第1四分位数が最小値寄り(箱ひげ図で左のひげが短い)であるはずである。
のほうが小さい値の都道府県が多く第1四分位数が最小値寄り(箱ひげ図で左のひげが短い)であるはずである。
すると、第1次産業で左のひげが短い![]() が2000年度、
が2000年度、
第3次産業で左のひげが短い![]() が1995年度(テ)(3点)である。
が1995年度(テ)(3点)である。
(3)トについて
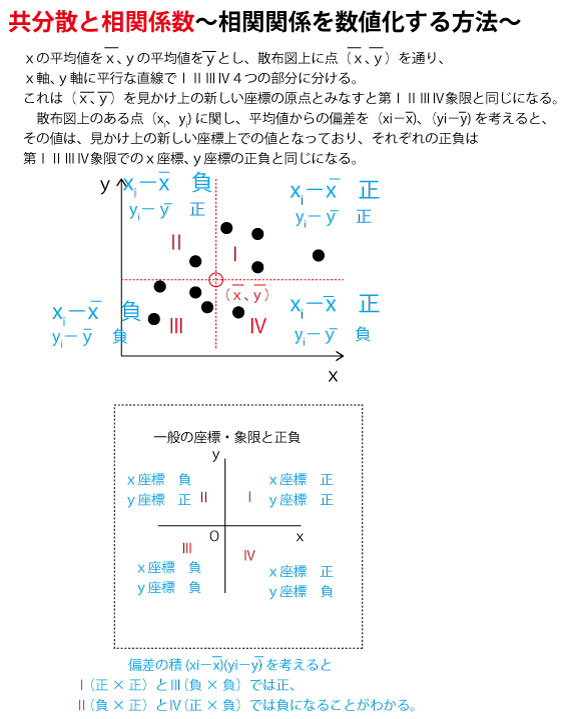
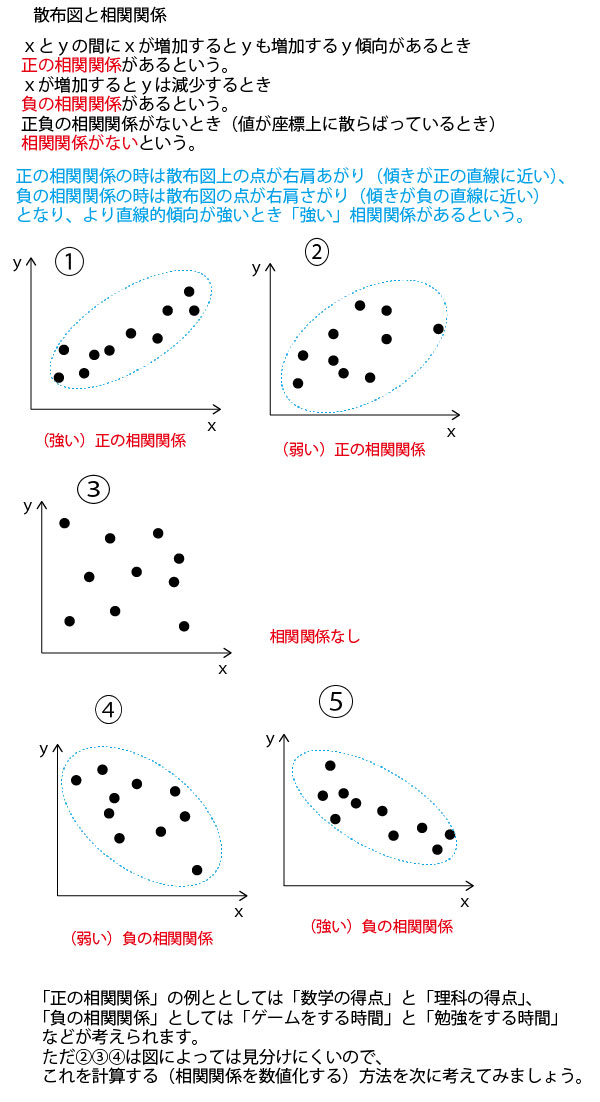
相関係数rは、-1≦r≦1であり、
負の相関関係が強いほどrは-1、正の相関関係が強いほどrは1に近づき、相関関係がない場合は0に近くなる。
問題文に、『「相関が強くなった」とは、相関係数の絶対値が大きくなったことを意味する。』とある。つまり正の相関関係、あるいは負の相関関係どちらかが強くなれば、「相関が強くなった」ことになる。
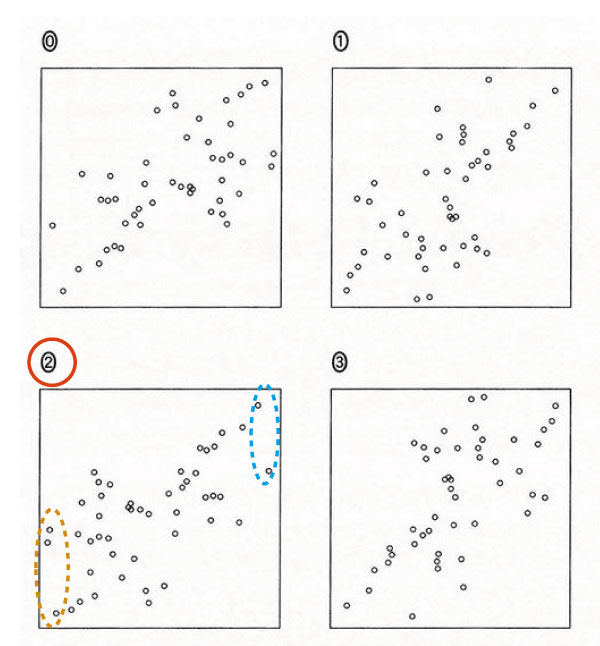
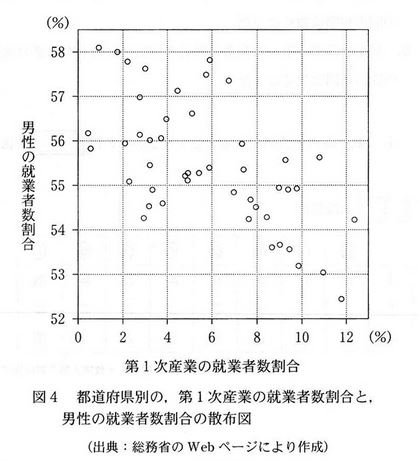
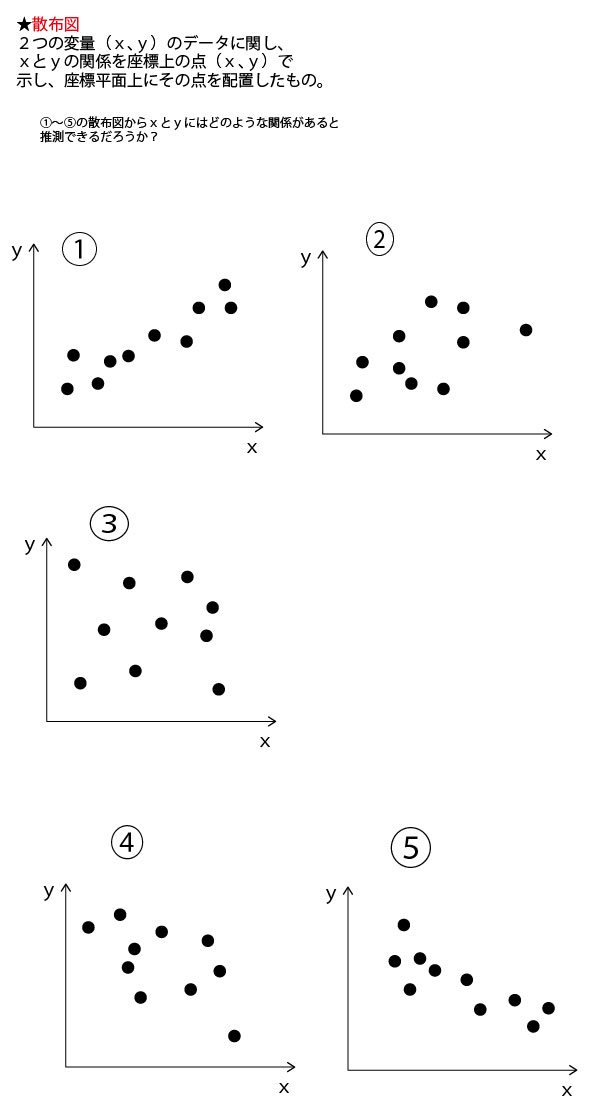
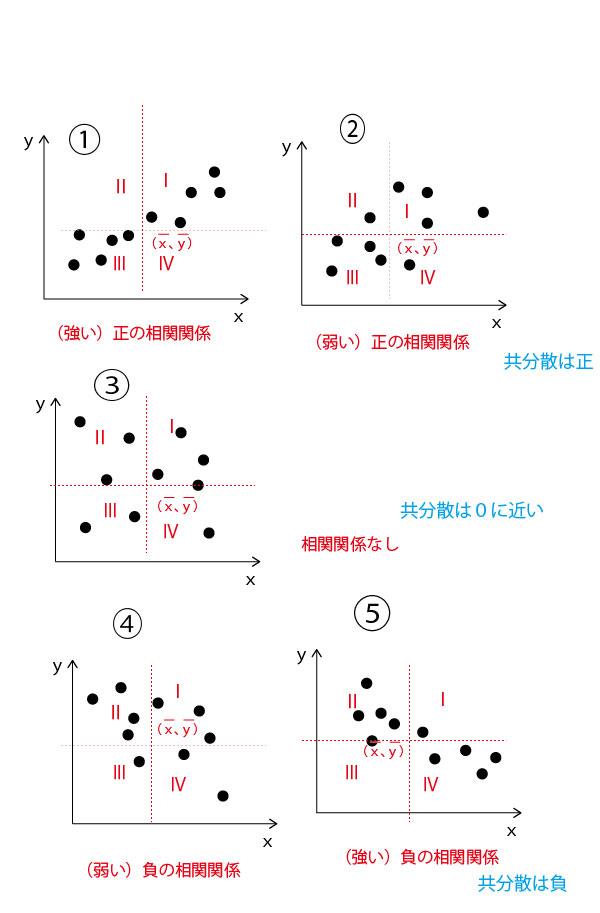
散布図ではより分散的なほうが相関が弱く、より直線的なほうが相関が強い。1975年度から2015年度への変化を散布図で見てみよう。
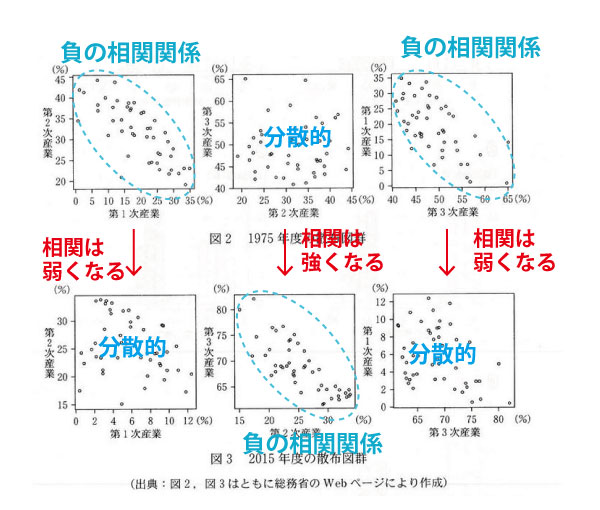
【発展学習】
ここからは、数学ではなく、社会的な分析となる。数学で統計分野(statistics)が重視されているのは、現実の社会現象を数学(統計)の力で分析し、社会問題を把握・対策していく手法を身に着けてほしいからという流れもあるので、この散布図の、1975年度→2015年の変化を解釈してみよう。
第1次産業(農業、林業と漁業)、第2次産業(鉱業、建設業と製造業)、第3次産業(前記以外の産業)となっているが、第3次産業の具体例としては、飲食店(サービス業)、コンピューター・ネット産業(製造ではなくてソフト)、運輸業(宅急便など)あたりをイメージするとよいかもしれない。
1975年度において、第1次産業と第2・3次産業が負の相関関係となっているのは、1960年代以降の高度経済成長期を経て、日本の主に農業人口の減少分が、そのまま都市や工業地区における第2・3次産業に従事者に移行した影響と考えられる。(土地利用でいえば田畑が、第2・3次産業の従事者の住宅や工業団地などに変化した影響と考えられる)。したがって農業人口比率が比較的維持された県では、第2・3次産業への移行は少なく、農業人口が減った県では第2・3次産業への移行が多い「負の相関関係」となる。一方、1975年当時は、サービス業などの第3次産業は未発達で、第2と第3の間ではそのような移動は少なく相関関係はなかったと考えられる。
しかし、その後40年を経て2015年度になる過程で、日本は第2次産業から第3次産業(コンピューター・ネット産業(製造ではなくてソフト)、運輸業(宅急便など))への大幅な移行がおきる。したがって第2次産業と第3次産業は負の相関関係となる。一方、第1次産業従事者は少なくなりながら固定化し、他への大幅な移行は少なくなくなり、相関関係がなくなってきた。
このように、散布図から社会的変化を読み取ることができる。
(3)ナについて
設問に「各都道府県の、男性の就業者数と女性の就業者数を合計すると就業者数の全体となることに注意する」
とヒントが書かれている。図は縦軸が%なので
男性の就業者数割合+女性の就業者割合=100%と考えれば、下図のように、図を50%で折り返して描いた(線対称の)図が女性の就業者割合の散布図になることがわかる。
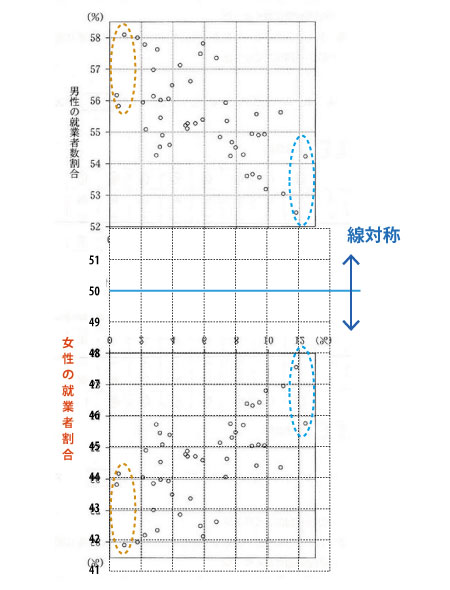
男性が負の相関関係なので、女性は正の相関関係となる。ただし選択肢の図はいずれも「正の相関関係」であることは同じなので、図の概形だけでは選べない。したがって点の正確さで見てみる。たとえば、横軸の値が少ない側の3点(図のオレンジ点線)と多い側の2点(図の青点線)を正確に反映しているという視点で見てみる。
と選ぶことができる。(注目点は他の点でもよい。)
【社会的考察】(一例)
これ以降は数学の問題ではなく、社会の問題である。また見方は様々ありうるので以下に私が述べることだけがすべてではないので、皆さん自身考えてみてほしい。
第1次産業の比率とその就業者の中の女性の比率が「正の相関関係」ということは何を意味するのだろうか?少数になりながら維持している第一次産業において、第1次産業の比率が高い県ほど、女性の就業者割合が大きいということは、ある程度農業が維持されている県では、家族(夫婦)労働で農業を維持している(単身男性で農業をしている例は少ない)と考えられるかもしれない。少ない県においては男性比率が大きいのは、どういう影響だろうか?東京都・大阪府などでは、家族経営というより、個人の大規模経営で単品を大量生産しており、その個人経営の従業者が男性が多いということなのか?あするはの漁業の比率の影響か?漁業は農業に比べ男性の比率が高い(女性の参画が難しい就労形態がある)。この視点で更に各県の第1次産業内の職種における男女比を調べ、改善点を探る考察につなげることができる。
↓以下は基礎知識のまとめです。
★【中学(中1「資料の整理」)】分野のまとめ

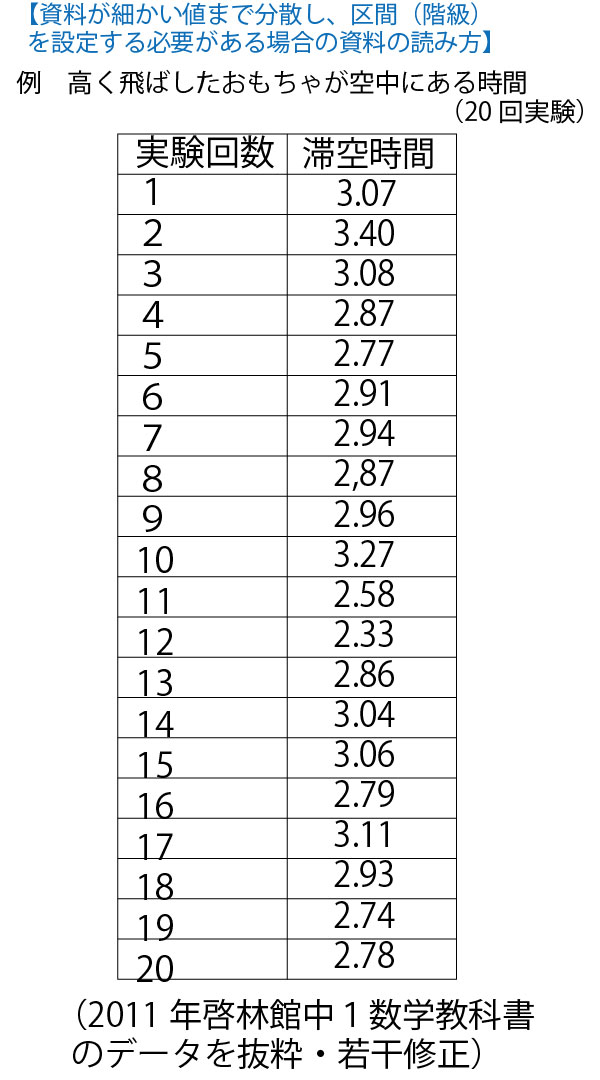

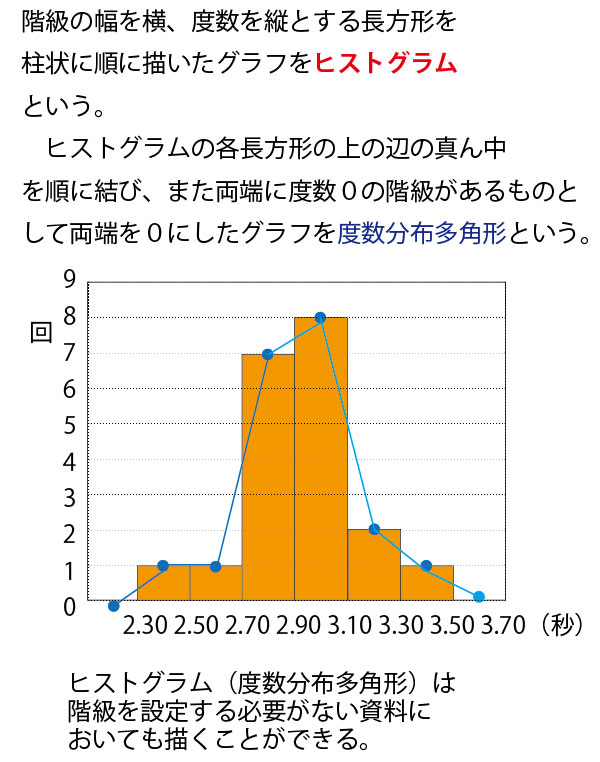
★高校数Ⅰ(データの分析)分野のまとめ。
中学1年で学ぶ「資料の整理」の発展編であり、この学問分野を統計学という。
具体例として、数学の小テスト(10点満点)の平均点がいずれも5点が分布が異なる30人の7クラス(1組~7組)を例に考えていこう。
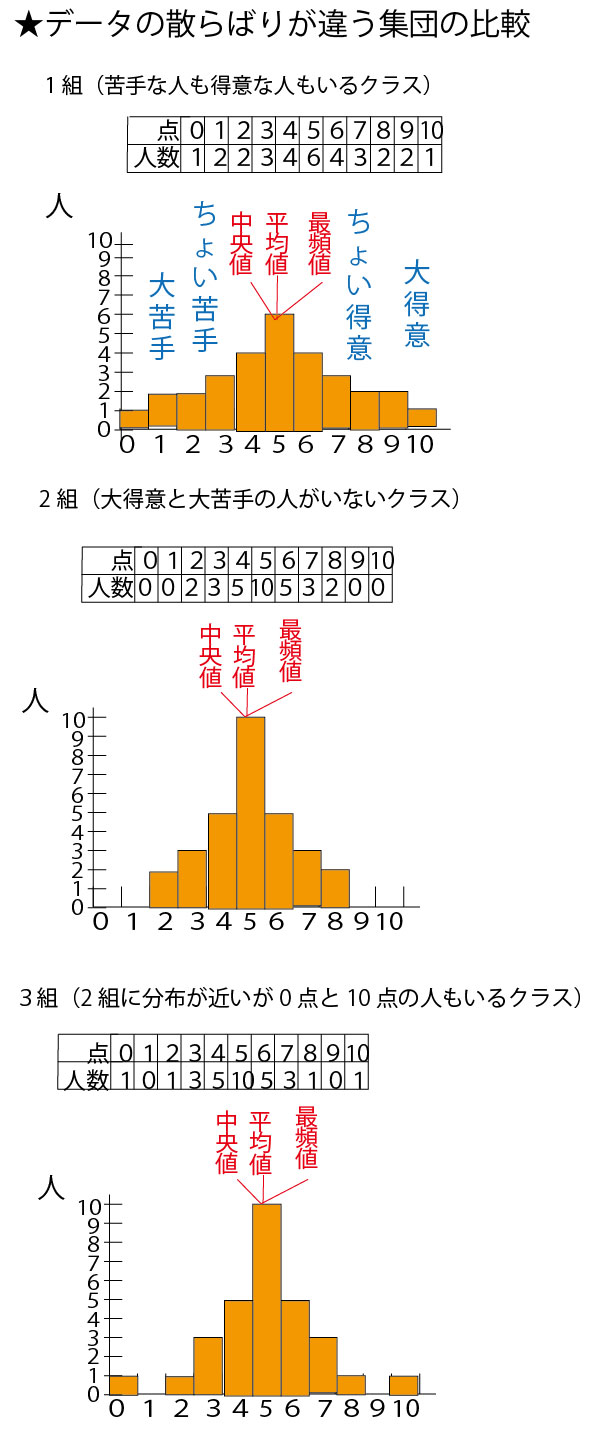
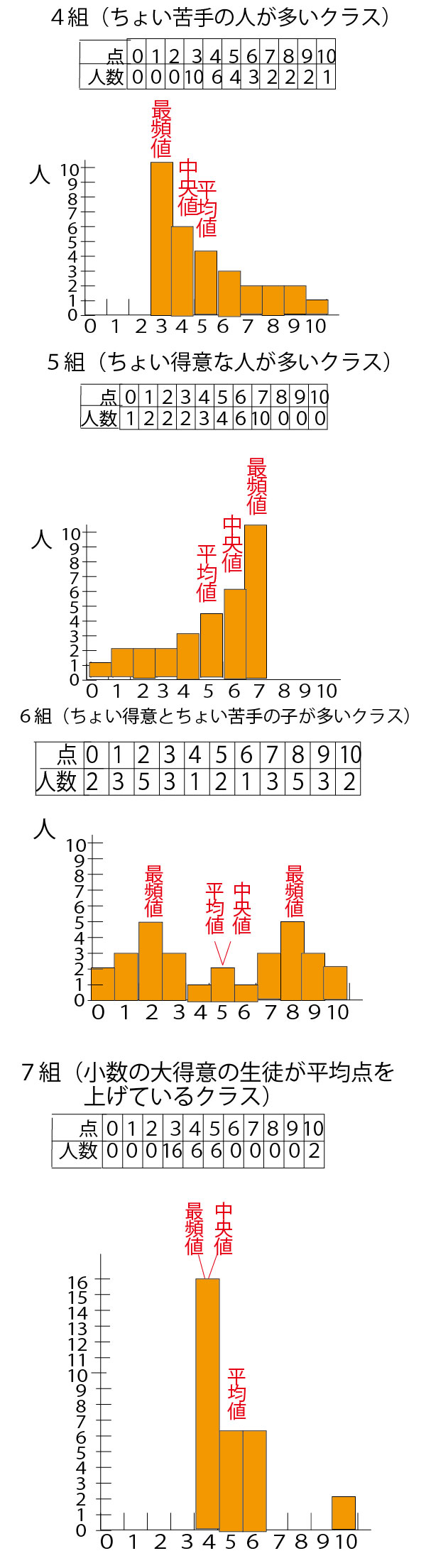


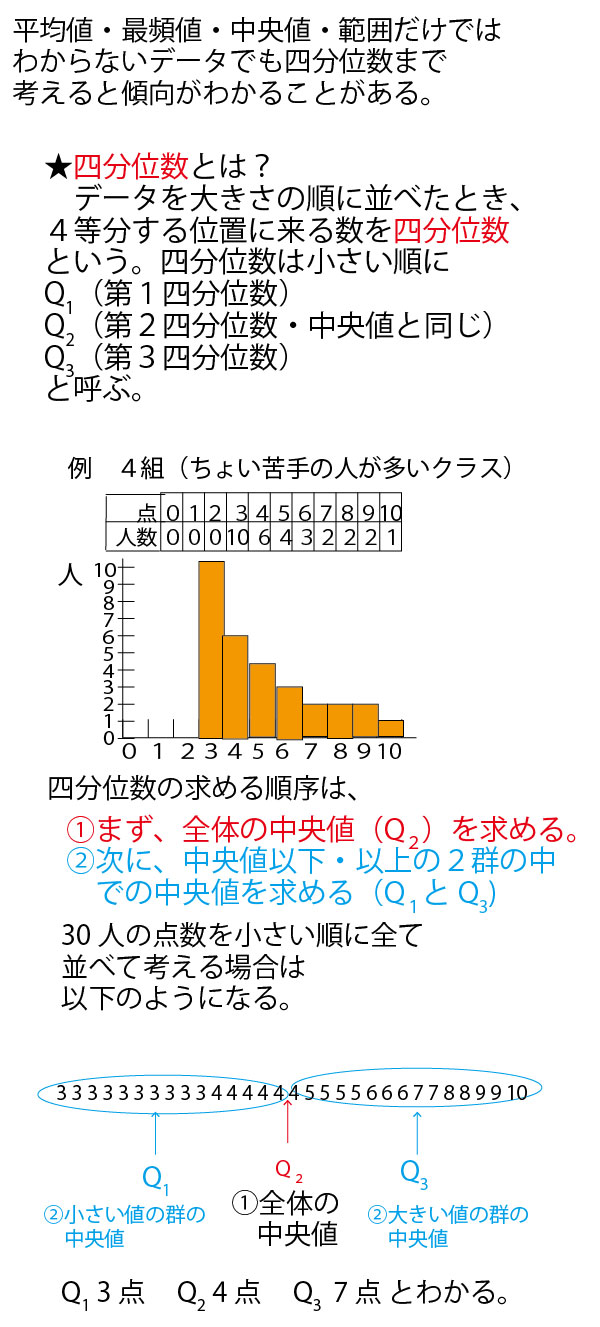
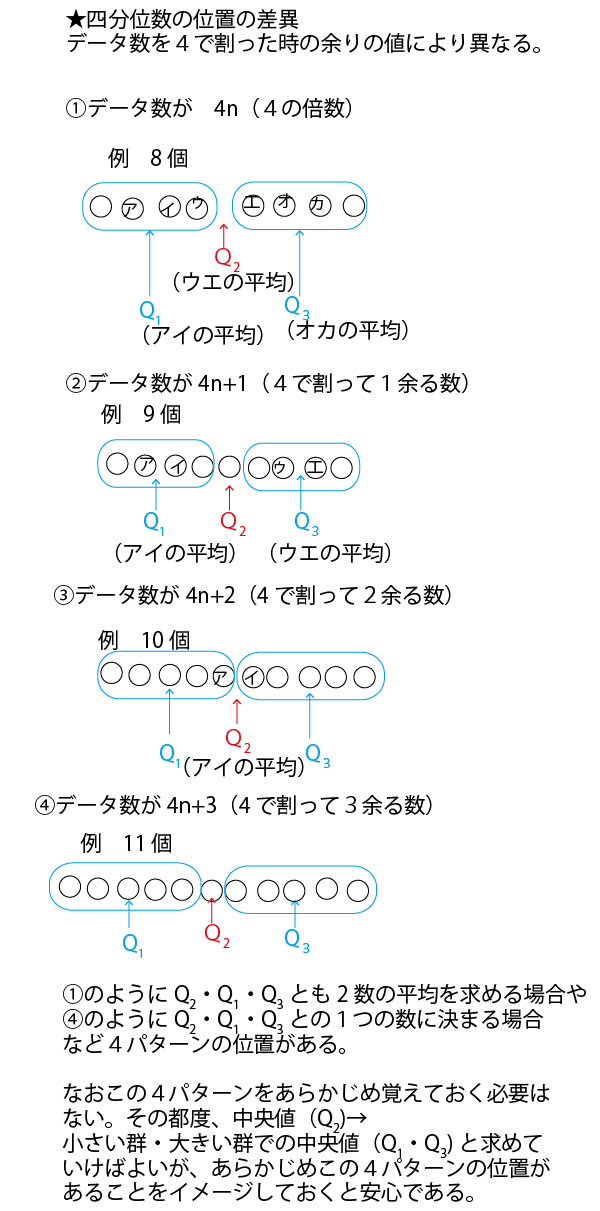




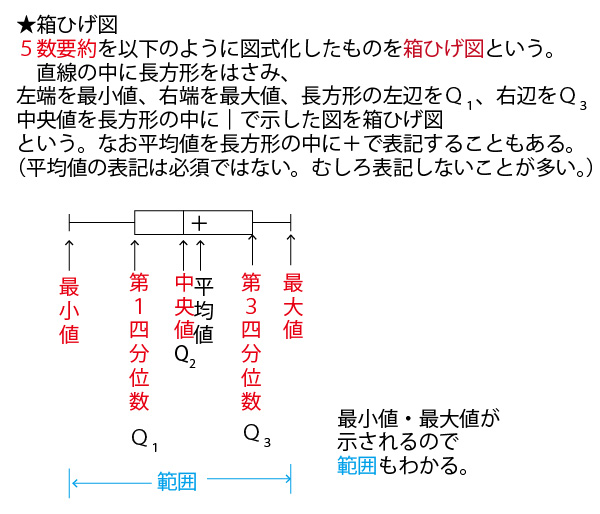
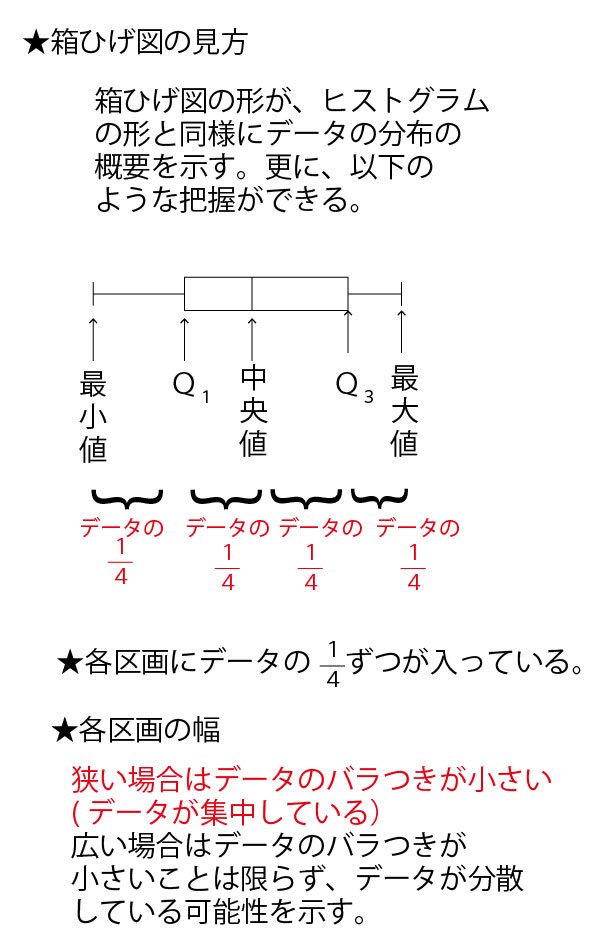
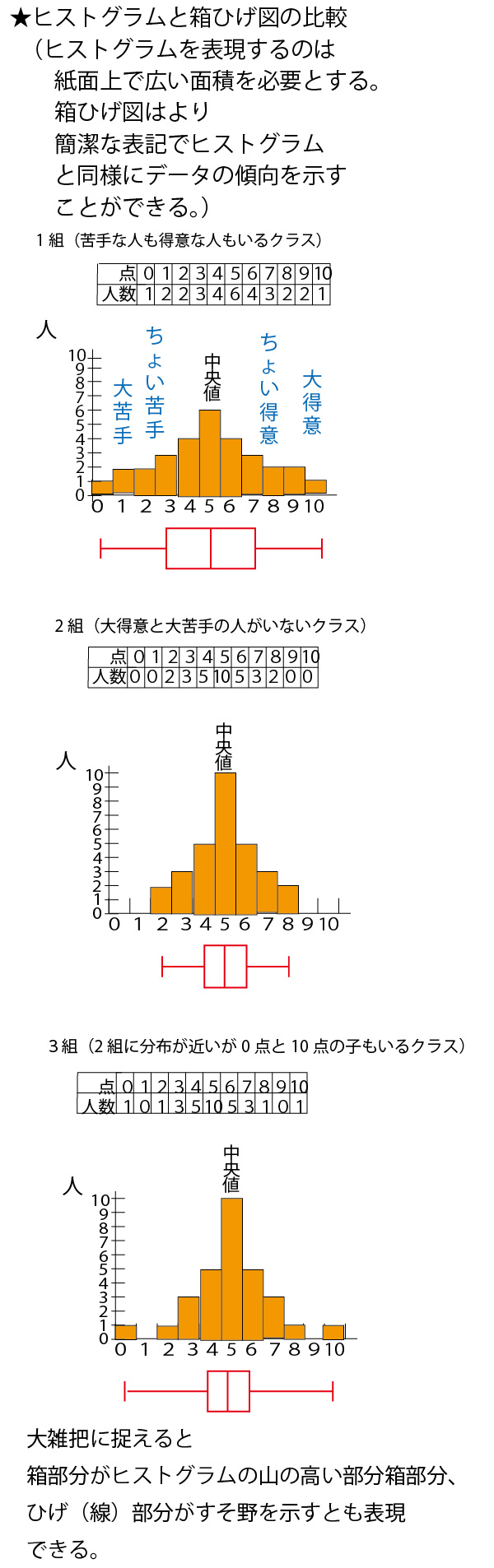
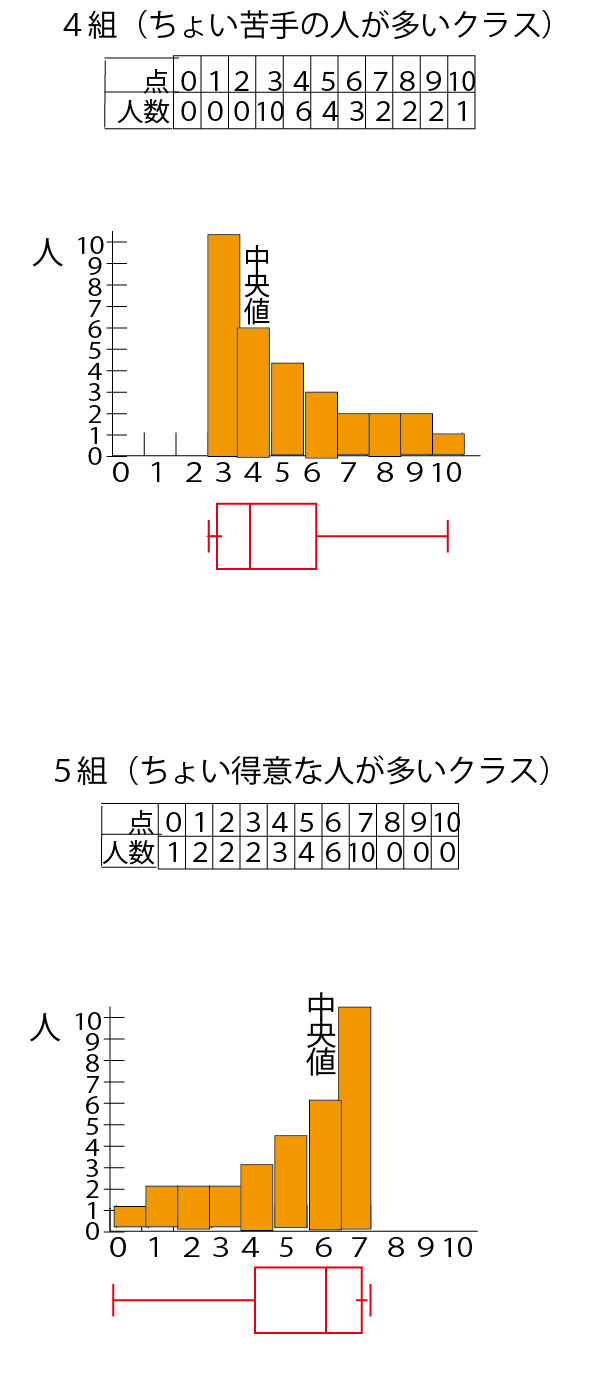
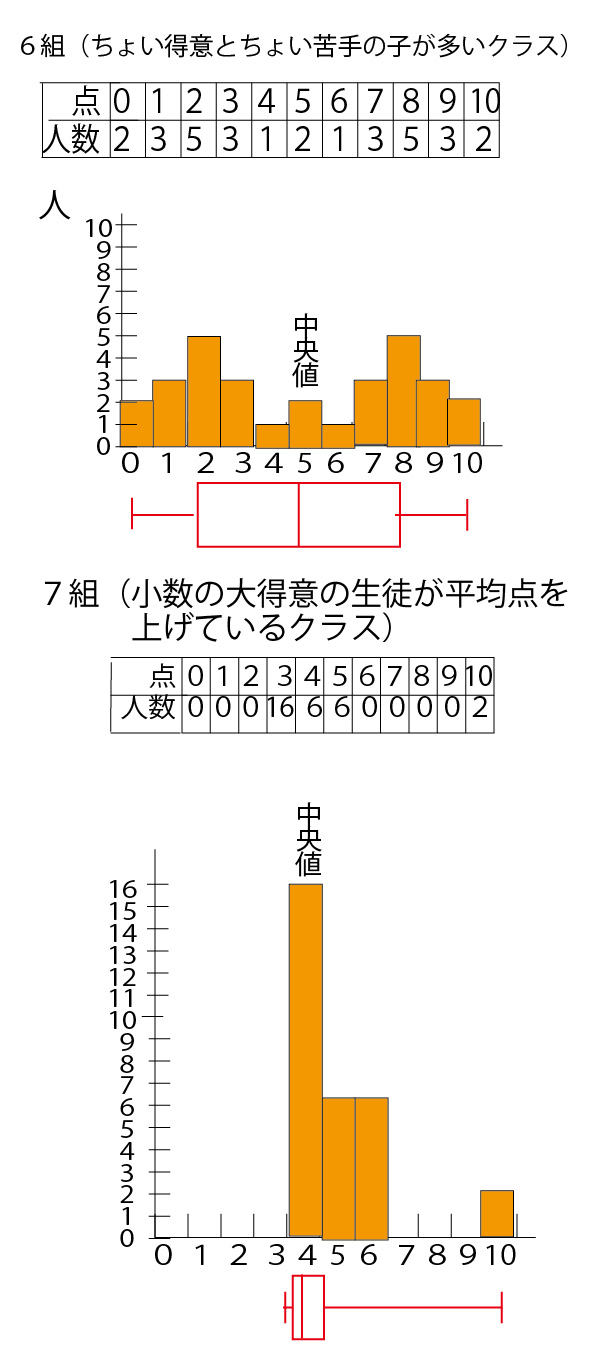
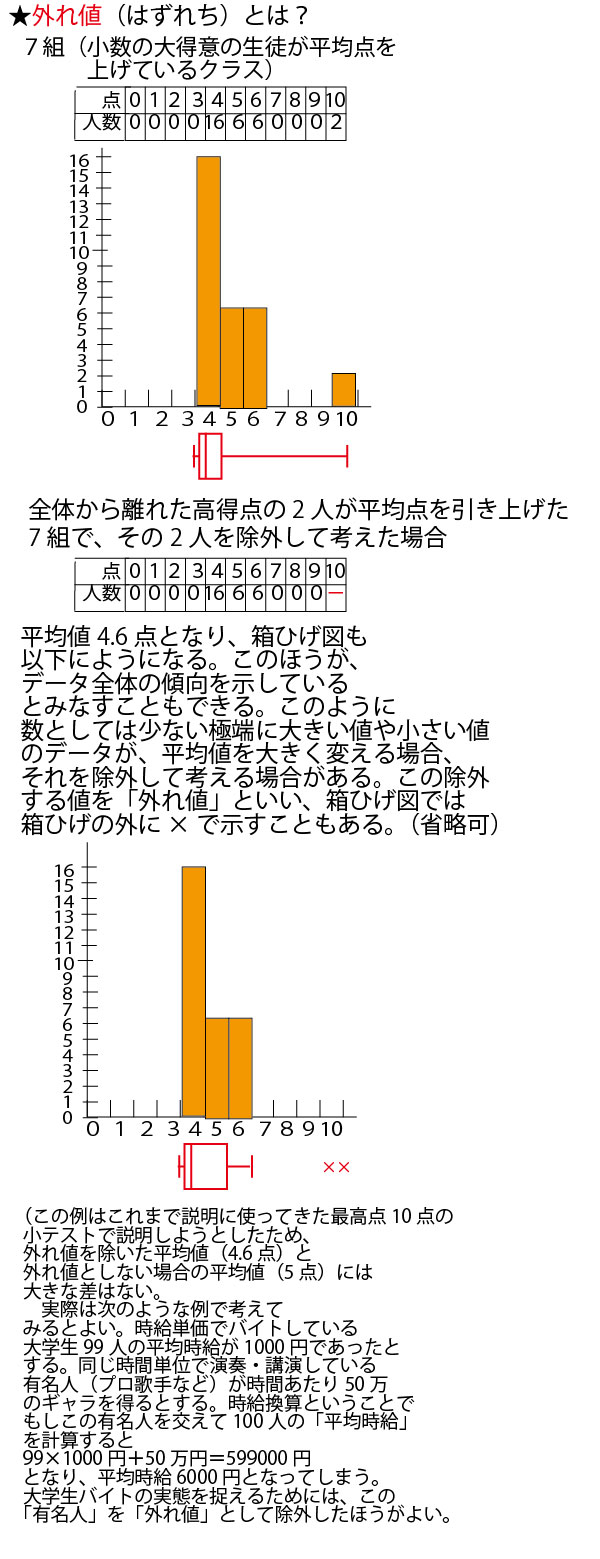

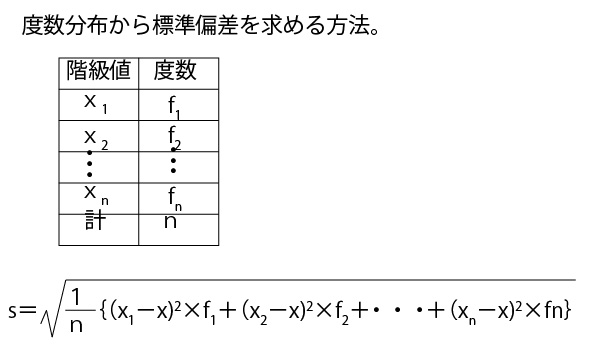
分散・標準偏差に関しては、最初に考えるのは30人クラスでは大きすぎて考えにくいので、まずは、平均点がいずれも5点となる5人組の5班(1班~5班)を例に考えていこう。





●関連大学入試共通テスト・センター試験解答解説
●2021年大学入試共通テスト「数学IA」第1問[1](因数分解・2次方程式の解の公式など)(配点10点)問題・解答・解説
●2021年大学入試共通テスト「数学IA」第1問[2](図形・三角比・余弦定理・正弦定理など)(配点20点)問題・解答・解説
●2021年大学入試共通テスト「数IA」第2問[1](短距離走におけるストライド・ピッチ・タイムの関係)(配点15点)問題・解答・解説
●2021年大学入試共通テスト「数学IA」第4問「整数論」(配点20点・選択)問題・解答・解説
●2021年大学入試共通テスト「数学IA」第5問(選択・図形・配点20点)問題・解答・解説