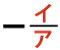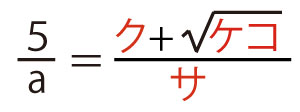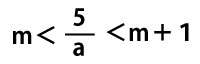2021年大学入試共通テスト「数学IA」第1問[1]（因数分解・２次方程式の解の公式など）（配点10点）問題・解答・解説

2021年1月26日　予備校講師、「円」「三角形」「図形の証明」著者、船橋市議　朝倉幹晴

2021年1月17日（日）に実施された大学入試共通テスト数学IA第1問［１］（ア～ス）（計10点）の問題・解答・解説です。同じ第1問でも［２］［３］（図形）（計20点）は実質的に別の問題なので、別に解答・解説を作りました。
●2021年大学入試共通テスト「数学IA」第1問[2]（図形・三角比・余弦定理・正弦定理など）（配点20点）問題・解答・解説

2021年受験生は２次試験に向けた復習に、2022年以降の受験生は来年の準備にご活用ください。
　実際の入試問題は白黒印刷ですが、画面上ですのでカラーを一部使いました。ア～スに当てはまる数字（０～９）を入れる形で答えてください。

大学入試共通テスト数学IA第1問［１］（配点10点）

[１]ｃを正の整数とする。ｘの２次方程式

2x²＋（4c－3）x＋２c²−c－11＝０・・・・

について考える。

（1）ｃ＝１のとき、　の左辺を因数分解すると

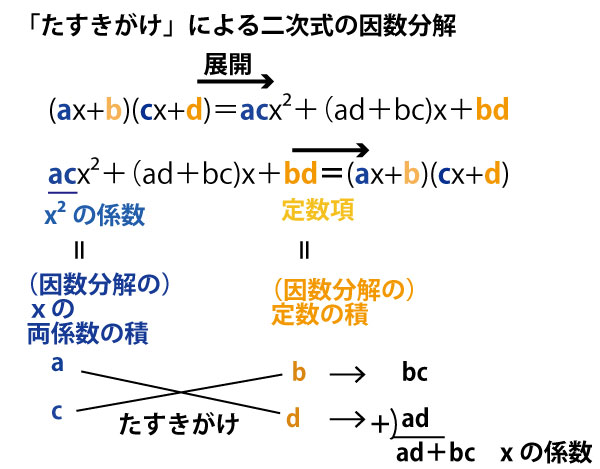
（アx + イ）（ｘ－ウ） （アイウ完答で2点）であるから、の解は

ｘ＝、ウ　　である。

（2）c=2のとき、の解は

　　 （エ～キ完答で2点）

であり、大きい方の解をaとすると

（ク～サ完答で2点）

である。　また、を満たす整数ｍはシ（2点）である。

（3）太郎さんと花子さんは、の解について考察している。

 

太郎：の解はｃの値によって、ともに有理数である場合もあれば、ともに無理数である          場合もあるね。ｃがどのような値のときに、解は有理数になるのかな。

花子：　2次方程式の解の公式の根号の中に着目すればいいんじゃないかな。

の解が異なる二つの有理数であるような正の整数ｃの個数はス個（2点）である。

[next_p]