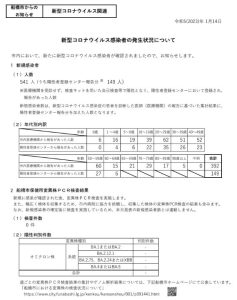
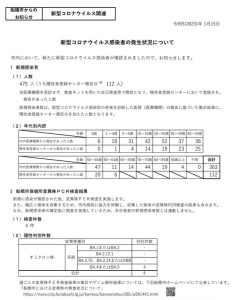
大学入試共通テスト2022年「数学ⅠA」第3問（確率）問題（選択・配点20点）・解答・解説

2023年1月14日 2023年3月26日

asakura

2023年1月　予備校講師・船橋市議　朝倉幹晴

大学入試共通テスト2022年「数学ⅠA」第3問（確率）問題（選択・配点20点）・解答・解説を作成しましたのでご活用ください。本文の最後をクリックすると解答・解説のページに飛びます。

大学入試共通テスト2022年「数学ⅠA」第3問（確率）問題（選択・配点20点）

複数人がそれぞれプレゼントを一つずつ持ち寄り、交換会を開く。ただし、プレゼントはすべて異なるとする。プレゼントの交換は次の手順で行う。

手順
外見が同じ袋を人数分用意し、各袋にプレゼントを一つずつ入れたうえで、各参加者に袋を一つずつでたらめに配る。各参加者は配られた袋の中のプレゼントを受け取る。交換の結果、1人でも自分の持参したプレゼントを受け取った場合は、交換をやり直す。そして、全員が自分以外の人の持参したプレゼントを受け取ったところで交換会を終了する。

（1）2人または3人で交換会を開く場合を考える。
2人で交換会を開く場合、1回目の交換で交換会が終了するプレゼントの受け取り方はア通り（1点）ある。したがって、1回目の交換で交換会が終了する確率はである。

3人で交換会を開く場合、1回目の交換で交換会が終了するプレゼントの受け取り方はエ通り（2点）ある。したがって、1回目の交換で交換会が終了する確率はである。
3人で交換会を開く場合、4回以下の交換で交換会が終了する確率はである。

（2）4人で交換会を開く場合、1回目の交換で交換会が終了する確率を次の構想に基づいて求めてみよう。

構想
1回目の交換で交換会が終了しないプレゼントの受け取り方の総数を求める。そのために、自分の持参したプレゼントを受け取る人数によって場合分けをする。

1回目の交換で、4人のうち、ちょうど1人が自分の持参したプレゼントを受け取る場合はサ通り（2点）あり、ちょうど2人が自分のプレゼントを受け取る場合はシ通り（2点）ある。このように考えていくと、1回目のプレゼントの受け取り方のうち、1回目の交換で交換会が終了しない受け取り方の総数はスセ（1点）である。
したがって、1回目の交換で交換会が終了する確率はである。