大学入試共通テスト2022年「数学ⅠA」第3問（確率）問題（選択・配点20点）・解答・解説

解説

 

交換会参加者を2人の場合はAB、3人の場合はABC、４人の場合をABCD、5人の場合をABCDEとする。ABCDEの持ってきたプレゼントをそれぞれabcdeとする。交換会では、本当はプレゼントさえ受け取れば各人が席を移動してもよいが、わかりやすくするため、２，３、4人が円卓テーブルで向かいあって座り、それぞれの席（AはA席、BはB席、CはC席、DはD席、EはE席）の卓の上で、プレゼントが置かれるイメージで考えよう。

2人交換会、3人交換会の「プレゼントの受け取り方」（配置）の可能性の全パターンを樹形図で考え、その中から1回目で交換会が終了する（全員が自分以外の人の持参したプレゼントを受け取る）か確率を考えよう。

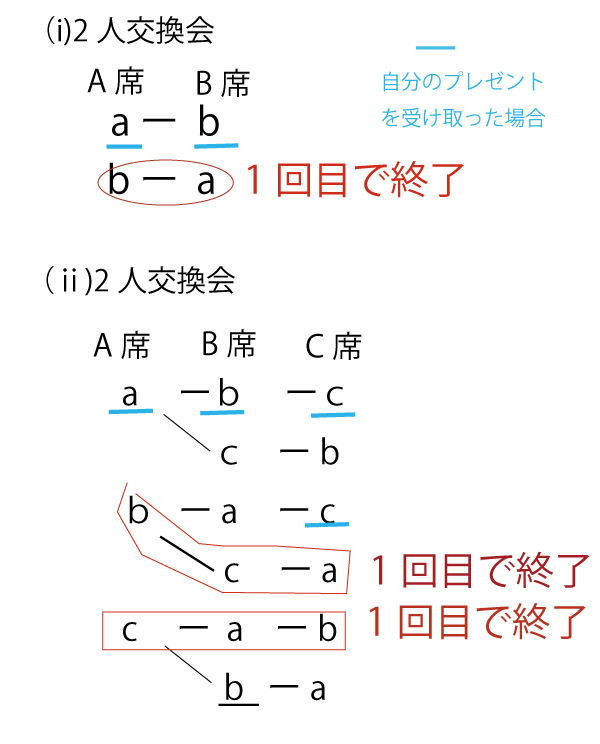
2人交換会　上図から、1回目で終了する受け取り方1通り（ア答）（1点）
　1回目で終了する確率は１／２（イウ答）（1点）

3人交換会　上図から、1回目で終了する受け取り方2通り（エ答）（2点）
図から受け取り方6通りなので、1回目で終了する確率は２／6＝１／３（オカ答）（1点）（1点）

4回以下の交換で交換会が終了する事象は、「4回連続終了しない事象」の余事象である。

 

（2）

共通テストの問題で、後半の小問を解くときは、それより前（多くは直前）に解いた結果を活用すると解きやすくなる（つまり前の小問の答は、次の小問のヒントになっている）ことが多い。

●ちょうど1人（のみ）が自分の持参したプレゼントを受け取る場合の数
ちょうど1人（のみ）が自分の持参したプレゼントを受け取るということは、残り3人は自分以外のプレゼントを受け取っていることになる。自分の持参したプレゼントを受け取ってしまった人を除く3人で考えると、その3人の中では自分以外のプレゼントを受け取っているので、その受け取り方は前問エと同じで2通りである。
自分のプレゼントを受け取ってしまったのが、A～Dの４通りあり、それぞれについて残り3人の中では受け取り方は2通りなので、
４通り（誰が自分のプレゼントを受け取ったか）×２通り（残り3人の中での受け取り方）＝８通りとなる。（サ答）（2点）

●２人が自分の持参したプレゼントを受け取る場合の数

2人が自分の持参したプレゼントを受け取るということは、残り2人は自分以外のプレゼントを受け取っていることになる。その受け取り方は前問アと同じで１通りである。
どの2人が自分のプレゼントを受け取ったかの組合せは

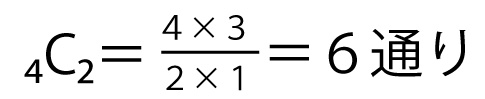
6通り（どの2人が自分のプレゼントを受け取ったか）×1通り（残り2人の中での受け取り方）＝６通り。（シ答）（2点）

同様に、次に「3人が自分の持参したプレゼントを受け取る場合」を考えてみるが、3人が自分の持参したプレゼントを受け取れば、残り1人も自分の持参したプレゼントを受け取ることになるので、「3人だけ」ということはありえないことがわかる。
最後に「4人全員が自分の持参したプレゼントを受け取る場合」はＡ-a、Ｂ-b、Ｃ-c、Ｄ-dの１通り。

交換会が終了しない受け取り方の総数は
1人のみが自分の持参したプレゼントを受け取る場合の数＋2人が自分の持参したプレゼントを受け取る場合の数＋4人とも自分の持参したプレゼントを受け取る場合の数
＝８＋６＋１＝15通り。（スセ答）（1点）

Ａ席、Ｂ席、Ｃ席、Ｄ席にプレゼントabcdを順に並べる事象なので、事象の全数は
₄Ｐ₄＝４×３×２×１=24

1回目の交換で交換会が終了する事象は、交換会が終了しない事象の余事象なので、

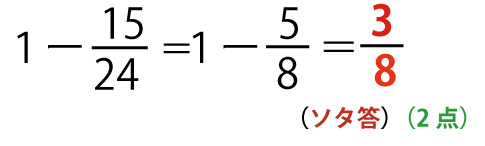
（3）
（2）で4人で行った作業を5人について考えればよい。

●ちょうど1人（のみ）が自分の持参したプレゼントを受け取る場合の数
ちょうど1人（のみ）が自分の持参したプレゼントを受け取るということは、残り4人は自分以外のプレゼントを受け取っていることになる。自分の持参したプレゼントを受け取ってしまった人を除く4人で考えると、その4人の中では自分以外のプレゼントを受け取っているので、その受け取り方は前問スセの余事象で、（24ー15）通り＝９通りである。
自分のプレゼントを受け取ってしまったのが、A～Eの５通りあり、それぞれについて残り４人の中では受け取り方は９通りなので、
５通り（誰が自分のプレゼントを受け取ったか）×９通り（残り3人の中での受け取り方）＝45通り。

●2人が自分の持参したプレゼントを受け取る場合の数

2人が自分の持参したプレゼントを受け取るということは、残り3人は自分以外のプレゼントを受け取っていることになる。その3人の中では自分以外のプレゼントを受け取っているので、その受け取り方は前問エと同じで2通りである。
どの2人が自分のプレゼントを受け取ったかの組合せは

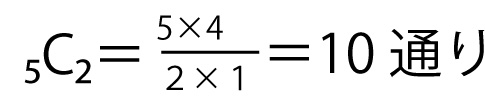
10通り（どの2人が自分のプレゼントを受け取ったか）×2通り（残り3人の中での受け取り方）＝20通り。

●3人が自分の持参したプレゼントを受け取る場合の数
3人が自分の持参したプレゼントを受け取るということは、残り2人は自分以外のプレゼントを受け取っていることになる。その受け取り方は前問アと同じで１通りである。
どの3人が自分のプレゼントを受け取ったかの組合せは

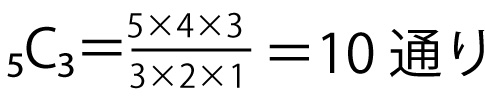
10通り（どの3人が自分のプレゼントを受け取ったか）×1通り（残り2人の中での受け取り方）＝10通り。

同様に、次に「4人が自分の持参したプレゼントを受け取る場合」を考えてみるが、4人が自分の持参したプレゼントを受け取れば、残り1人も自分の持参したプレゼントを受け取ることになるので、「4人だけ」ということはありえないことがわかる。
最後に「5人全員が自分の持参したプレゼントを受け取る場合」はＡ-a、Ｂ-b、Ｃ-c、Ｄ-d、E-eの１通り。

交換会が終了しない受け取り方の総数は
1人のみ自分のプレゼント＋2人＋3人＋5人とも自分のプレゼント
＝45＋20＋10＋１＝76通り

Ａ席、Ｂ席、Ｃ席、Ｄ席、E席にプレゼントabcdeを順に並べる事象なので、事象の全数は
₅Ｐ₅＝５×４×３×２×１=120

 交換会が終了する事象は交換会が終了しない事象の余事象なので、

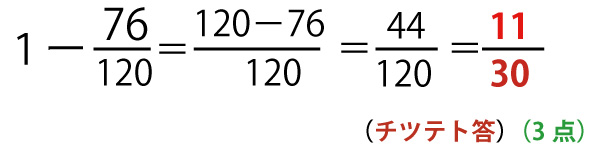
（4）ABCDがそれそれ自分以外のプレゼントを受け取る場合には以下の２つの場合がありうる。

●Eは自分のプレゼントeを受け取っている場合
前問スセで答えた、4人で交換会が終了しない受け取り方（15通り）の余事象（4人で交換会が終了する受け取り方）と同じなので、24ー15＝9通り

●A～E全員が自分以外のプレゼントを受け取っている場合
前問チツテトを求める時に考えた交換会が終了する事象なので44通り。

全部で９＋44＝53通りがこの場合となる。この中で講演会が終了するのは、A～E全員が自分以外のプレゼントを受け取った時なので、その条件付き確率は