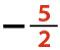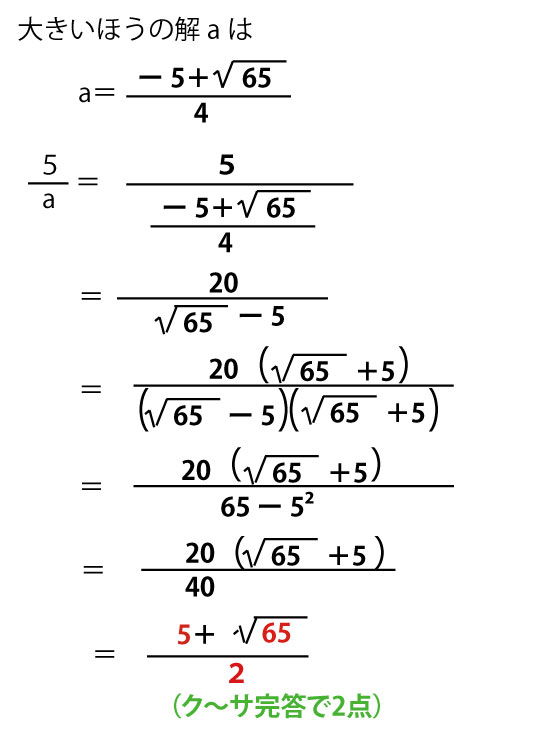2021年大学入試共通テスト「数学IA」第1問[1]（因数分解・２次方程式の解の公式など）（配点10点）問題・解答・解説

解説

［１］（1）
ｃ＝１の時、

2x²＋（4c－3）x＋２c²−c－11＝０にｃ＝１を代入すると
2x²＋（4×1－3）x＋2×1²−1－11＝０

2x²＋x＋2－1－11＝０

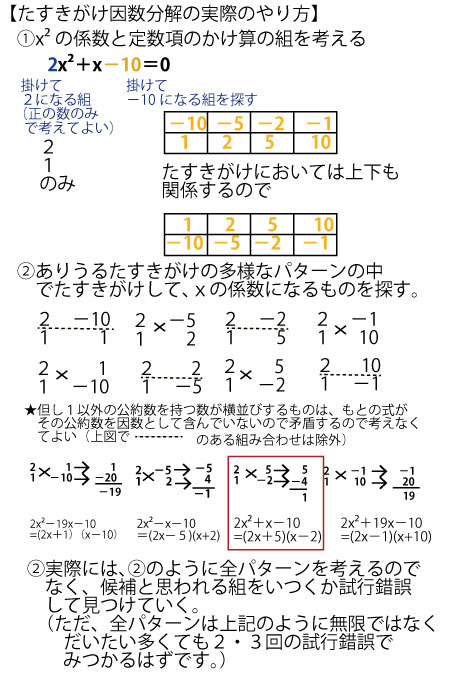
2x²＋x－10＝０
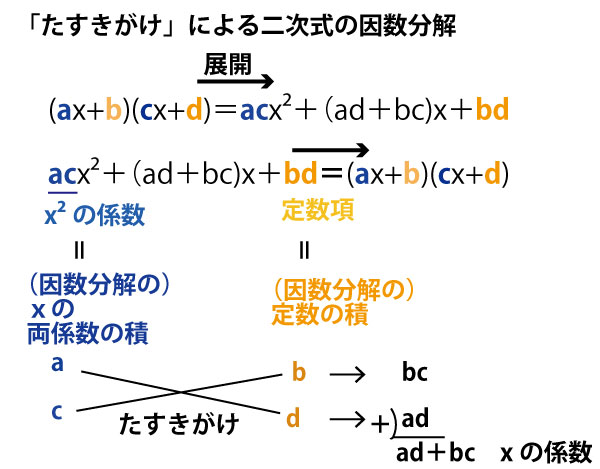
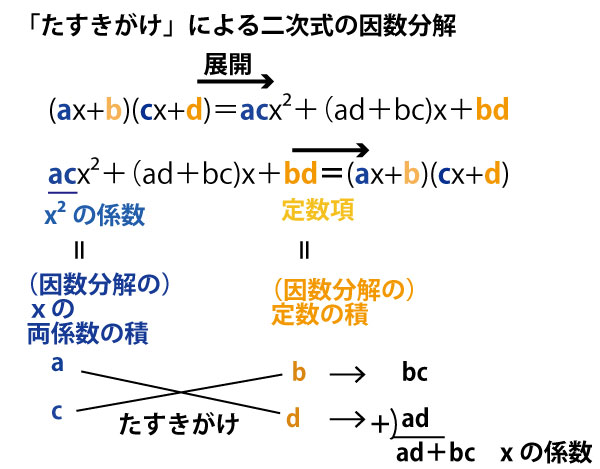
たすきがけで因数分解をすると
（2x＋５）（ｘ－2）＝０（アイウ完答で2点）

ｘ＝　、２

 

 

（2）ｃ＝２のとき

2x²＋（4c－3）x＋２c²−c－11＝０にｃ＝2を代入すると
2x²＋（4×2－3）x＋2×2²−2－11＝０
2x²＋5x＋8−2－11＝０
2x²＋5x－5＝０
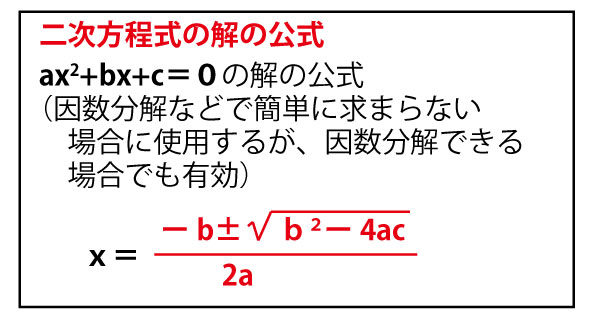
今度は二次方程式に解の公式が使われた答の形なので、因数分解しようと試みる必要はなく解の公式を当てはめる。

【追加解説】解の公式は、（たすきがけによる）因数分解ができる式においても有効である。したがってア～エの因数分解ができなかった場合には以下のように解の公式から解を求め、逆に因数分解をくみたてることもできる。（この解法よりも、たすきがけによる因数分解に慣れたほうが解答に要する時間が短い。したがってこのはあくまでもどうしてもわからなかった時のための念のための解法である。）

 

問題の解答の続きに戻ります。

（3）

以下、花子が言うとおり、根号の中のみを考える。
根号の中＝（4c－3)²−4×2×（2c²−c－11)

=16c²−24c＋9ー８（2c²−c－11)
＝16c²−24c＋9ー16c²+8c＋88

＝ー16c＋97＝97－16c

ｃは正の整数で根号（√）の中が負になる場合は数IAでは考えなくてもよい。また根号の中が０であると、√０＝０なので「解は異なる２つの有理数」とはならず、解は１つの有理数となってしまい、設問の条件に合わない。

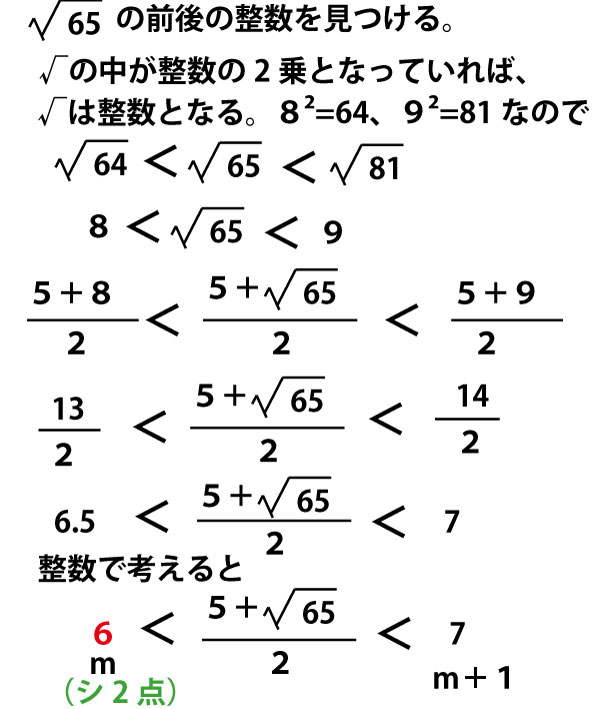
97－16c＞０でとり得るｃの値をすべて考えてみる。
ｃ＝１のとき　97－16c＝97ー16×1=97－16＝81=9²      （（1）で既に解いている）
c＝２のとき　97－16c＝97ー16×２＝97－32＝65（（2）で既に解いている）
c＝３のとき　97ー16ｃ＝97ー16×３＝97ー48＝49＝7²
ｃ＝４のとき　97ー16ｃ＝97ー16×４＝97－64＝33
ｃ＝５のとき　97ー16c=97ー16×5＝97－80＝17
ｃ＝６のとき　97ー16c＝97ー16×6＝97－96＝１＝１²

根号の中は正の整数の2乗ならば、根号は消えるので、解は２つの異なる有理数となる。
よって、そうなる正の整数ｃは３個（ｃ＝１、３、６）とである。（ス2点）

 

関連　大学入試共通テスト・センター試験「数学」解答・解説

●2021年大学入試共通テスト「数学IA」第1問[2]（図形・三角比・余弦定理・正弦定理など）（配点20点）問題・解答・解説
●2021年大学入試共通テスト「数IA」第2問［１］（短距離走におけるストライド・ピッチ・タイムの関係）（配点15点）問題・解答・解説
●2021年大学入試共通テスト「数学IA」第2問[２]（統計）問題・解答・解説配点15点）
●2021年大学入試共通テスト「数学IA」第4問「整数論」（配点20点・選択）問題・解答・解説
●2021年大学入試共通テスト「数学IA」第5問（選択・図形・配点20点）問題・解答・解説

●大学入試センター「数学」解答解説（一部）