2021年大学入試共通テスト「数学IA」第1問[2]（図形・三角比・余弦定理・正弦定理など）（配点20点）問題・解答・解説

2021年1月30日 2022年6月2日

asakura

2021年1月　予備校講師、「円」「三角形」「図形の証明」著者、船橋市議　朝倉幹晴

2021年1月17日（日）に実施された大学入試共通テスト数学IA第1問［２］（セ～ヒ）（計20点）の問題・解答・解説です。同じ第1問でも［１］（因数分解・2次方程式の解の公式など）（ア～セ）（計10点）は実質的に別の問題なので、別に解答・解説を作りました。↓

2015～18年大学入試センター数学IA第2問「図形と三角比」部分（配点15点）問題・解答・解説
実際の入試問題は白黒印刷ですが、画面上ですのでカラーを一部使いました。セ～ヒに当てはまる数字（０～９）あるいは選択肢の番号を入れる形で答えてください。

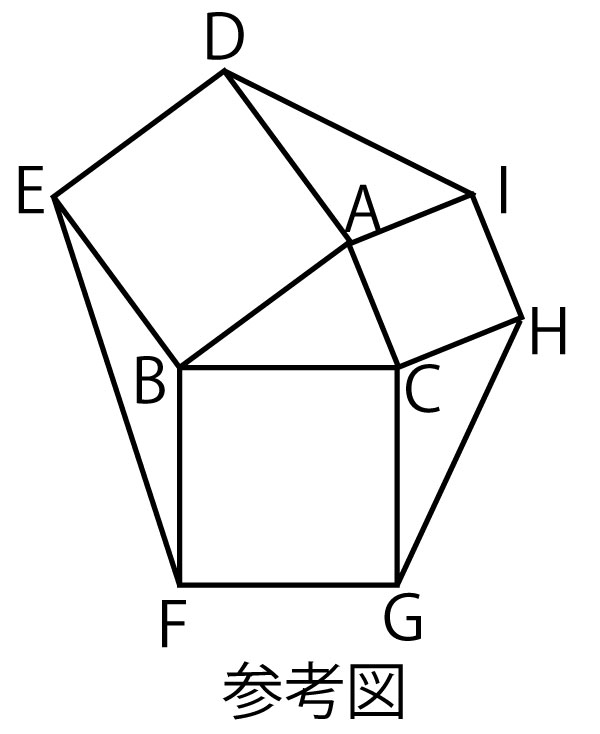
[２]図のように、△ＡＢＣの外側に辺ＡＢ、ＢＣ、ＣＡをそれぞれ1辺とする正方形ADEB、BFGC、CHIAをかき、2点EとF、GとH、IとDをそれぞれ線分で結んだ図形を考える。以下において

BC＝a、CA＝b、ＡＢ＝c

∠ＣＡＢ＝Ａ　∠ＡＢＣ＝Ｂ、∠ＢＣＡ＝Ｃ

とする。

（1）ｂ＝６、ｃ＝５、cosA＝のとき、sinA＝（2点）であり、

△ＡＢＣの面積はタチ（2点）、△ＡＩＤの面積はツテ（2点）である。

（2）正方形ＢＦＧＣ、ＣHＩＡ、ＡＤＥＢの面積をそれぞれＳ_１、Ｓ_２、Ｓ_３とする。このとき、Ｓ_１－Ｓ_２－Ｓ_３は

・０°＜Ａ＜90°のとき、ト（1点）。

・Ａ＝90°のとき、ナ（1点）。

・90°＜Ａ＜180°のとき、ニ（1点）。

ト～二の解答群（同じものを繰り返し選んでもよい。）

０である

正の値である

負の値である

正の値も負の値もとる

(3) △ＡＩＤ、△ＢＥＦ、△ＣＧＨの面積をそれぞれＴ_１、Ｔ_２、Ｔ_３とする。このとき、ヌ（3点）である。

ヌの解答群

a<b<cならば、Ｔ_１＞Ｔ_２＞Ｔ_３

a<b<cならば、Ｔ_１＜Ｔ_２＜Ｔ_３

Ａが鈍角ならば、Ｔ_１＜Ｔ_２かつＴ_１＜T_３

a、b、cの値に関係なく、Ｔ_１＝Ｔ_２＝Ｔ_３

（4）△ＡＢＣ、△ＡＩＤ、△ＢＥＦ、△ＣＧＨのうち、外接円の半径が最も小さいものを求める。

０°＜Ａ＜90°のとき、ＩＤネＢＣであり （2点）

（△ＡＩＤの外接円の半径）ノ（△ＡＢＣの外接円の半径）（2点）

であるから、外接円の半径が最も小さい三角形は

・０°＜Ａ＜Ｂ＜Ｃ＜90°のとき、ハである。（2点）

・０°＜Ａ＜Ｂ＜90°＜Ｃのとき、ヒである。（2点）

ネ、ノの解答群（同じものを繰り返し選んでもよい。）

＜　＝　＞

ハ、ヒの解答群（同じものを繰り返し選んでもよい。）

△ＡＢＣ　△ＡＩＤ　△ＢＥＦ　△ＣＧＨ

[next_p]