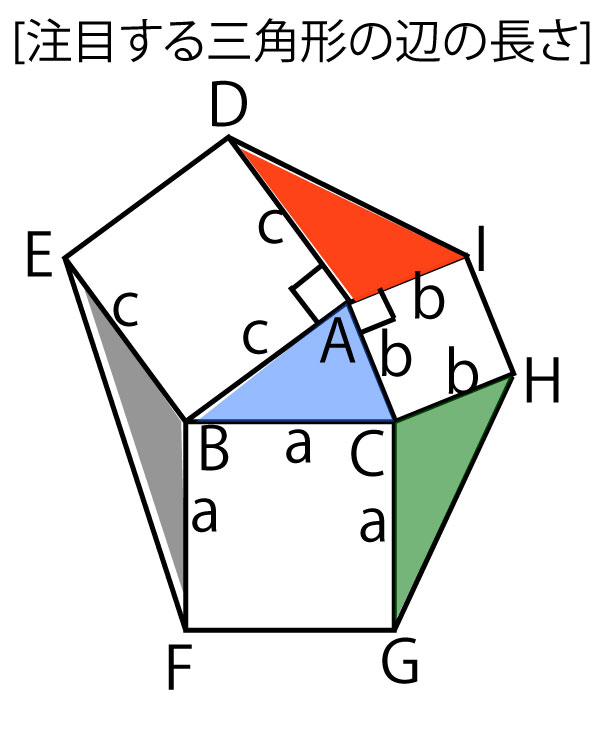
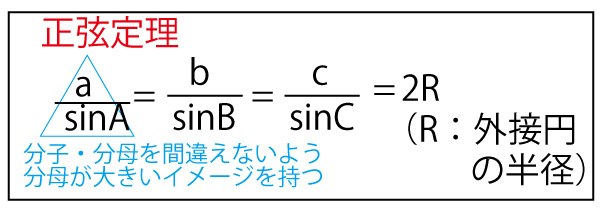2021年大学入試共通テスト「数学IA」第1問[2]（図形・三角比・余弦定理・正弦定理など）（配点20点）問題・解答・解説

2021年1月30日 2022年6月2日

asakura

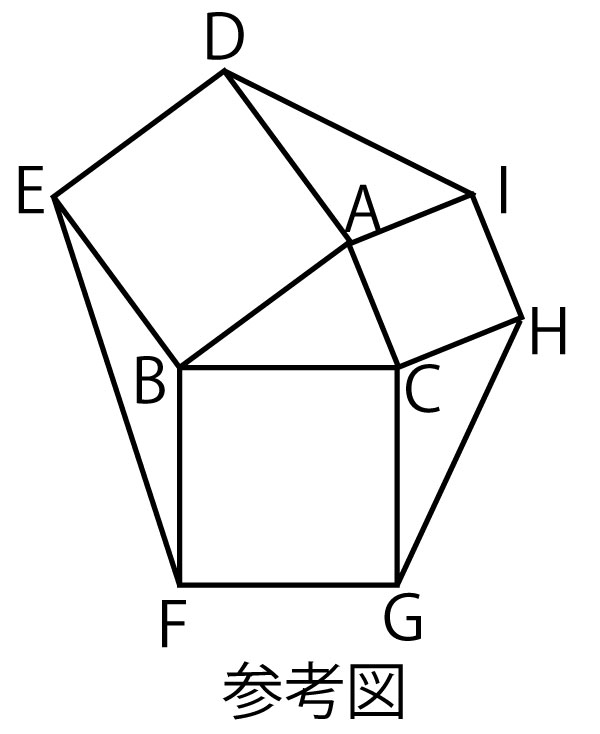
解説

　問題文の冒頭にある、BC＝a、CA＝b、ＡＢ＝c、∠ＣＡＢ＝Ａ　∠ＡＢＣ＝Ｂ、∠ＢＣＡ＝Ｃ、表記は以下のように中学数学から高校数学以降で表記が変更される点なので慣れてほしい。

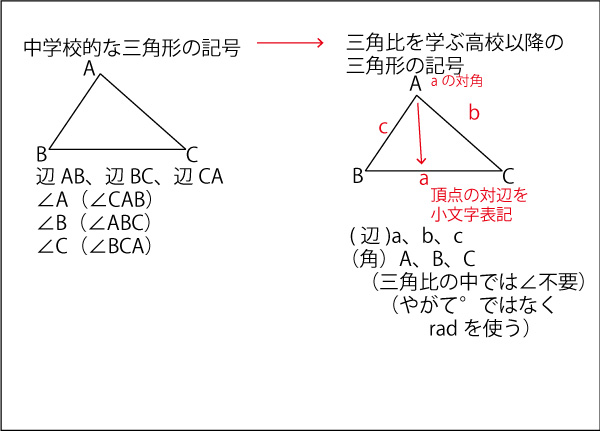
次に三角比（数Ⅱ以降は三角関数）や角の定義が高校数学で数１前半→数１後半→数２と変化する流れを理解してほしい。本問題は数１であるが、次に示した数２の基本線を知っておいたほうが解きやすい。まずはそれを説明した上で問題を解いていこう。

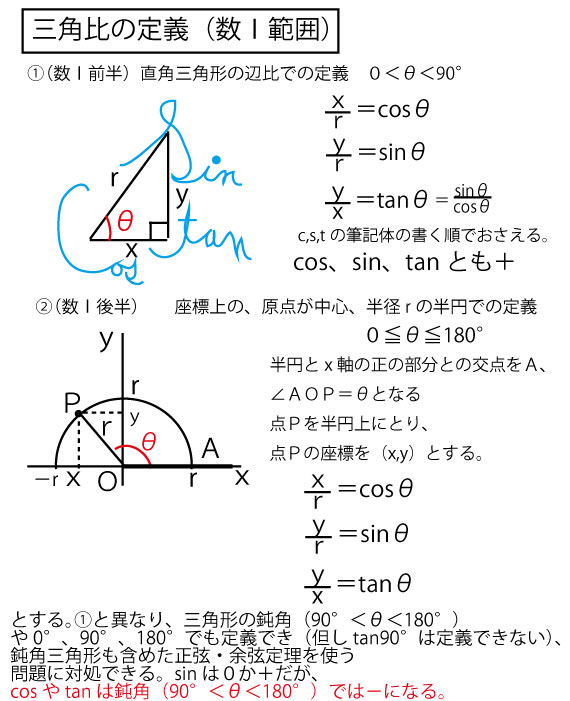
高校数学では角をθ（シータ）で示すことが多い。数Ⅰも最初はcos、sin、tanの定義は「直角三角形の１つの鋭角」（０＜θ＜90°）の周りの辺比に注目するという三角形に縛られた定義である。しかし、後半の定義では、直角三角形（の１つの鋭角）に縛られず、鈍角（90°＜θ＜180°）でも定義できるようになる。

次に、数２範囲での三角関数（三角比を拡大して把握したもの）の理解の初歩とその前提としての角の捉え方の変化を教えておこう。

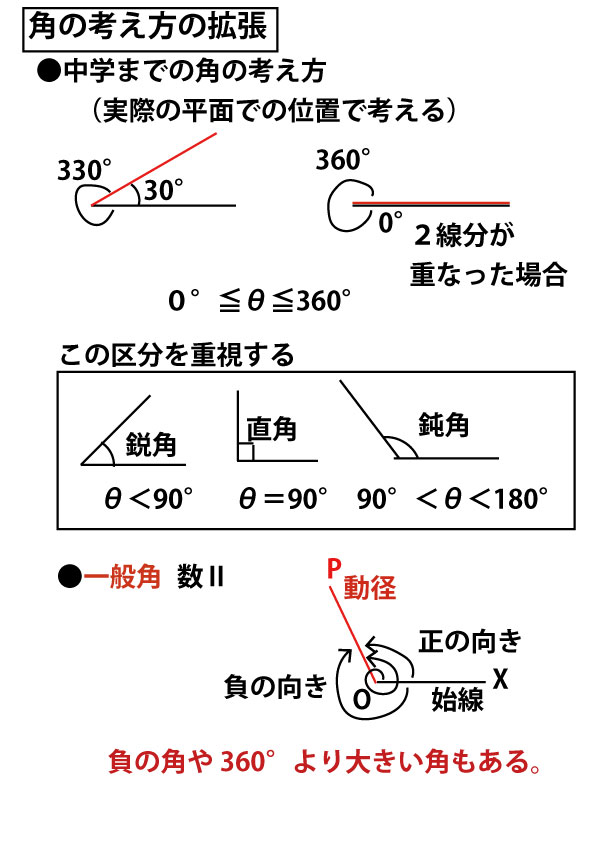
高校の数２においては、基準となる半直線OX（始線）、半直線OPをOの周りに回転させたときの角が角の定義となる。反時計回りを「正の角」、時計回りを「負の角」とし、1回転以上に回転させることも可能なので、360°以上の角もありうる。たとえば480°の角とは360°＋120°なので、実質は120°の角と同じことになる。負の角や360°を超える角も可能となるこの定義を「一般角」とい

う。さて、この一般角に角の考え方を拡張した場合の、cos、sin、tanはどう定義するのか？
数２においては、単位円（座標上で原点を中心とする半径１の円）と角θの動径の交点で定義する。（単位円の考え方は数１でも少し紹介されているが、本格的に活用するのは数２である）

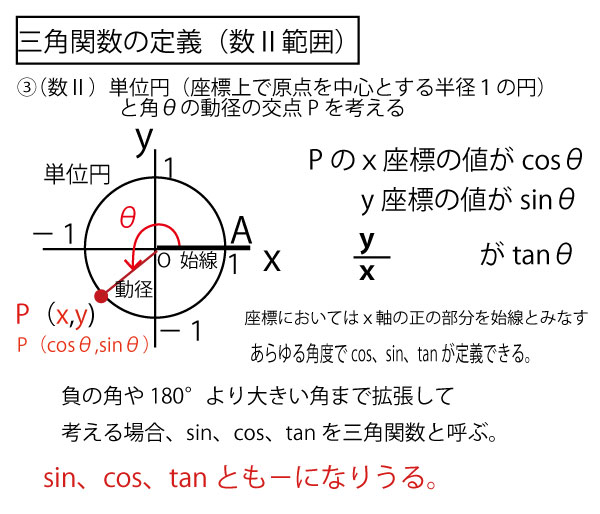
このように、ＯＰ（長さ１）が原点Ｏを中心に回転し、Ｐが単位円の円周上をθ回転した時、Ｐのｘ座標、ｙ座標が、cosθ、sinθと考えられる。この場合、角は負の角や180°より大きい角でも定義できるので、cos、sin、tanをもともと三角形の辺比の意味する「三角比」から「三角関数」と表現する。何回転しても角の定義ができることは、特に物体・天体・機械における回転運動、そして、回転運動の視野で考えると分析しやすい波の運動や往復運動などを考えやすくなり、数学が自然科学一般に応用しやすくなる。

次にこの拡張したsin、cos、tanの正負を考えてみよう。数１ではとくに180°より大きい角は聞かれず、数２で本格的には使うものであるが、イメージだけでも持っておくと、数１を解くバックグランンドとなる。青字で書いた０°・90°・180°・270°の節目のcos、sinの値にも注目しておいてほしい。（とりわけ数１では、cos90°＝０、sin90°＝１は知っておきたい）

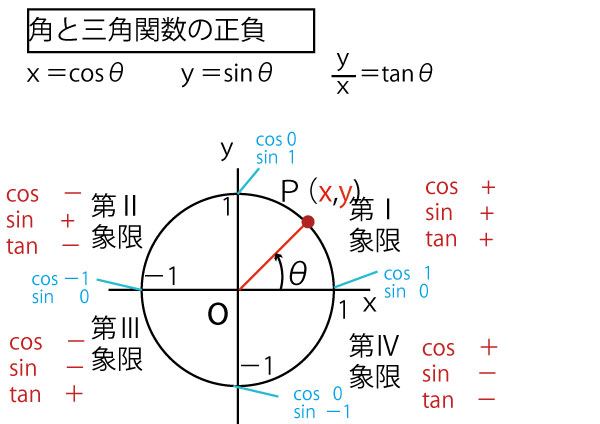
数１では鈍角（90°＜θ＜180°）に関連して、θに対し（180°ーθ）のcos、sin、tanの値がどうなるかを聞かれることが多いので、単位円の上半分の半円で考えて、以下の関係は把握しておきたい。

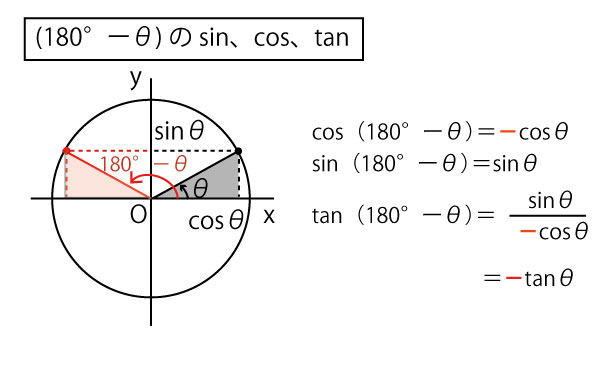
θを考えた灰色の三角形をｙ軸に関して折り返した赤の三角形が（180°ーθ）を考えるヒントとする。灰色三角形と赤三角形は合同なので辺の長さは同じで、座標上の位置で正負のみが変換しうる。cos（x座標）は正負が逆転するが、sin（y座標）は正負は逆転しない。

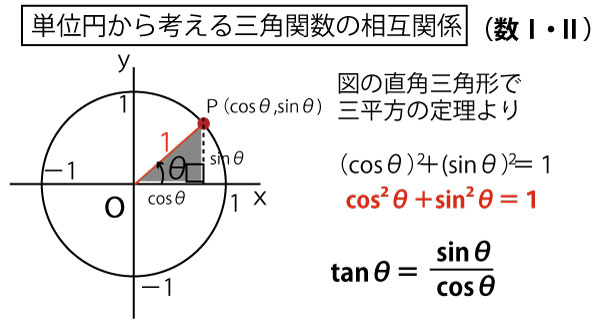
また、単位円におけるcos、sin、tanの定義から以下の三角関数の相互関係が成り立つ。

(cosθ）²、（sinθ）²、(tanθ）²は、cos²θ、sin²θ、tan²θと表記するのは一般的な表記法とされている。

ここから問題を解いてみる。

次にsinを活用した三角形の面積の求め方を確認しよう。

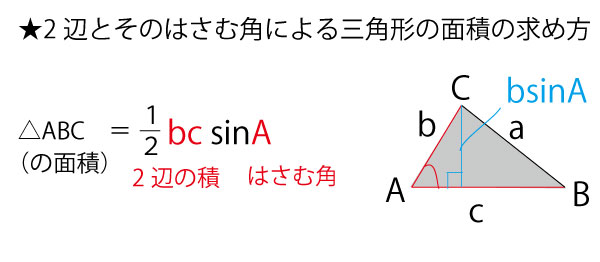
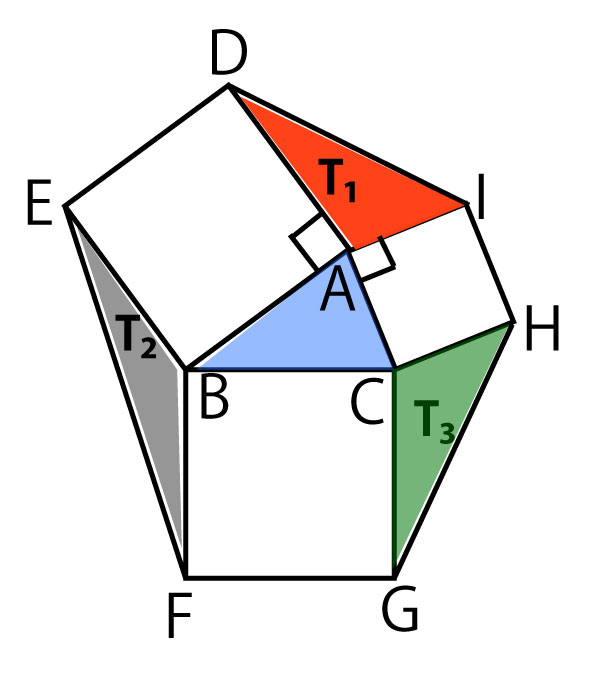
それでは問題で求めるべき２つの三角形に注目してみよう。

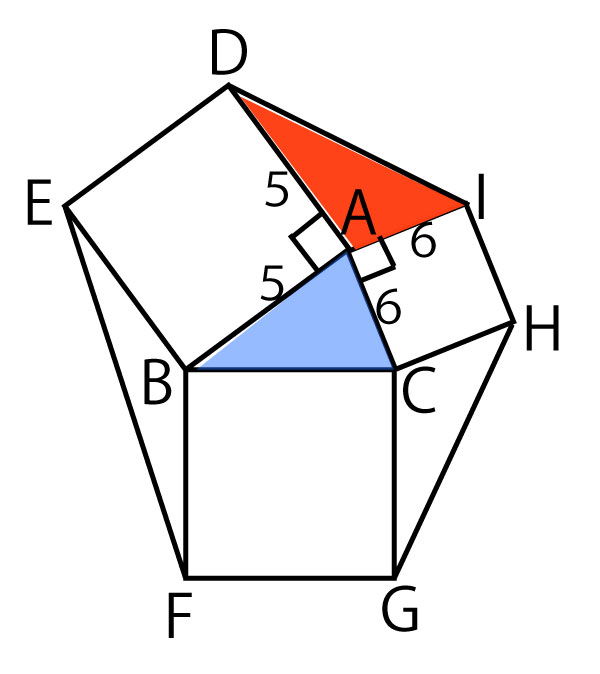
（なお図を見ると、ABのほうがACより長く見えるのに、AB＝５、AC＝６はおかしいと思う人がいたかもしれない。私自身もたしかに間違ったかと思い何度が見返したがこの設定である。ただし（1）の問題文に「ｂ＝６、ｃ＝５、cosA＝のとき」とあくまで一例であることが明記してあるし、問題文における図は、思考するための材料として出題者が付記した図なので、現実の長さや角度を必ずしも正確に反映しているとは限らない。したがって問題の数値設定どおりに計算すればよい。）

中心の青三角形△ABCと上の赤三角形△AIDの面積を求める問題であるが、前問で、sinAを求めさせているので、sinを使う面積公式を使えばよい。△ABCは以下のようになる。

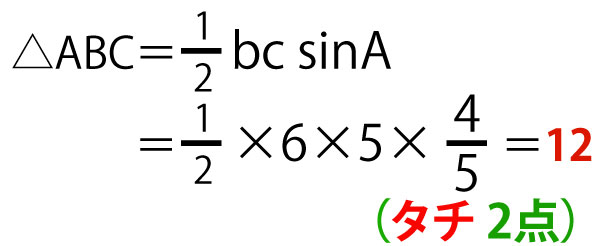
赤三角形△AIDを求めるためには、両側にある四角形ADEB、CHIAが正方形であること、その辺や角の特徴を活用するとともに先に説明したsin（180°ーθ）＝sinθを活用する。

（2）の解説に入る前に余弦定理・正弦定理を整理しておこう。余弦（cos）と辺の長さに関する定理を「余弦定理」、正弦（sin）と辺の長さに関する定理を「正弦定理」といい、数１でよく聞かれる定理である。以下の説明のように三角形の6構成要素（３辺、３角）のうち、少なくとも1辺を含む３要素が与えられると残りの３要素を求めることができ、その状況において以下の例のように両定理をうまく使い分ける。

（2）で聞かれている３つの正方形の面積S_１、S_２、S_３はa²、b²、c²であることに気づいてほしい。

（なお（1）で使ったb=6、c=5の値はあくまで（1）でだけの値である。（2）からの設問が一般的なa、b、ｃという長さの文字表記に移行していることから、移行の問題でb=6、c=5は使ってはいけない。設問（1）で「ｂ＝６、ｃ＝５、cosA＝のとき、」となっていることがそれを示している）

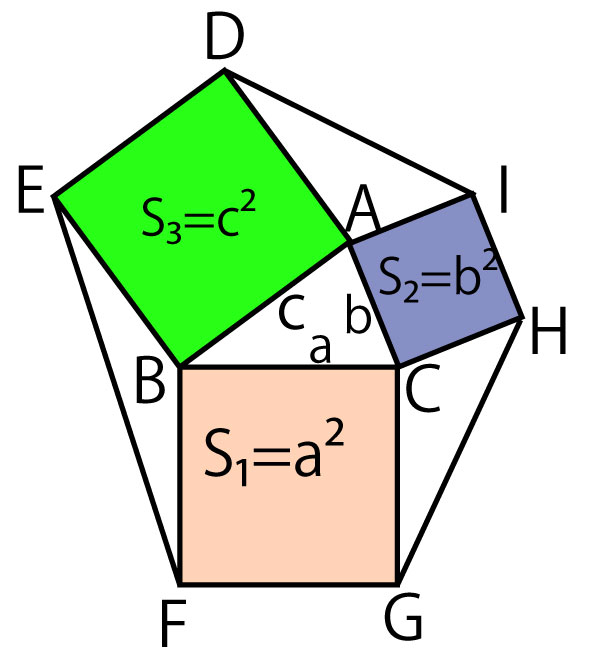
そうすれば、S_１－S_２－S_３＝a²−b²－c²とわかり、余弦定理の形に近いことがわかる。
これまでAに注目してきたので、aとA中心の余弦定理を考えてみる。

2bcは正なので、設問で求めるべきS_１－S_２－S_３＝a²−b²－c²の正負はcosAの正負と逆になる。

Aが鋭角（０°＜A＜90°）ならば、cosAは正なので、S_１－S_２－S_３＝a²−b²－c²は負となる。ト（1点）

A＝90°ならば、cosA＝０なのでS_１－S_２－S_３＝a²−b²－c²は０となる。。ナ（1点）

ちなみにa²−b²－c²＝０、つまりa²＝b²+c²つまり直角三角形（A＝90°）における三平方の定理を示していることになる。
つまり、中学で学んだ三平方の定理は、余弦定理において注目する角が90°となった場合の特殊例とも考えられる。

Aが鈍角（90°＜A＜180°）ならば、cosAは負なので、S_１－S_２－S_３＝a²−b²－c²は正となる。ニ（1点）

（3）前の問題で示した△ABC＝△AID（T_１）（面積が等しい）は長さが等しい2辺を持ち、ある頂点で対面する角がθと180°ーθに相当しsinの値が同じである場合なら常になりたつ。つまり、頂点Bで対面している△ABC＝△ＢＥＦ（T₂）、頂点Cで対面している△ABC＝△ＣＧＨ（T_３）。よって,つねにT_１＝T₂＝T₃。（ヌ　3点）

（4）最後に外接円の半径の4問を考えよう。外接円の半径なので、正弦定理を使うことは類推できる。

ネで問われているＩＤとＢＣの長さの比較はIDとBCを余弦定理で求めてみる。
△ABCに注目した余弦定理で
BC²＝AC²＋AB²−2AC・AB・ cosA＝b²＋c²−2bc cosA
△ADIに注目した余弦定理で
ID²＝AI²＋AD²−2AI・AD・ cos∠DAI＝b²＋c²−2bc cos（180°ーA）＝b²＋c²−2bc （－cosA）＝b²＋c²＋2bc cosA

0＜A＜90°なので　cosAは正の値（cosA>0)。よって2bccosAも正の値（2bccosA>0)
よってID²＞BC²
辺の長さは正の値なのでID＞BC（ネ　2点）

△ＡＩＤの外接円と△ＡＢＣの外接円の比較について、正弦定理の２Rは直径なのでまず直径で比較してみる。
sinA＝sin（180°ーA）なので、

ネ・ノでは求めたように、△ABCは鋭角Aと△AIDの鈍角180°−AがAで対面している場合は、外側の三角形（△AID）の外接円の半径ほうが大きいとわかった。
△ABCの角がすべて鋭角の場合には
０°＜Ａ＜Ｂ＜Ｃ＜90°の場合、同様な関係が△ABCとBで対面する△BEF、Cで対面する△CGHにもあるので、それぞれ外側の三角形（△BEF、△CGH）の外接円の半径のほうが大きい。したがって外接円の半径が最も小さい三角形は△ABCとなる。（ハ　、2点）

０°＜Ａ＜Ｂ＜90°＜Cの場合、

A、Bは鋭角なので、△ABCとAで対面する△AID、Bで対面する△BEFの中では、△ABCの外接円の半径が最も小さくなる。
しかし、Cは°鈍角なので、△ABCとCで対面する△CGHの∠GCHは鋭角になる。鈍角側の三角形の外接円の半径のほうが大きくなるので、鈍角であるCの側の△ABCの外接円の半径のほうが、△CGHの外接円の半径より大きい。つまり△CGHの外接円の半径は、△ABCの外接円の半径より小さく、４つの三角形の中で△CGHの外接円の半径が最小となる。
（ヒ　2点）

★↓本設問のような円や三角形に関する基礎的な事項の理解のため、拙著「円」「三角形」をぜひお読みください。