2022年千葉県公立高校入試「数学」第2問（一次関数・二次関数）（配点15点）問題、解答、解説

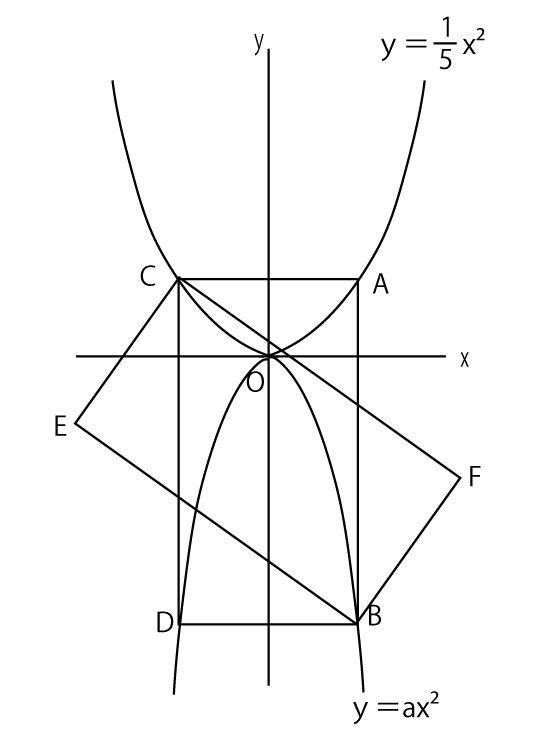
【解説】

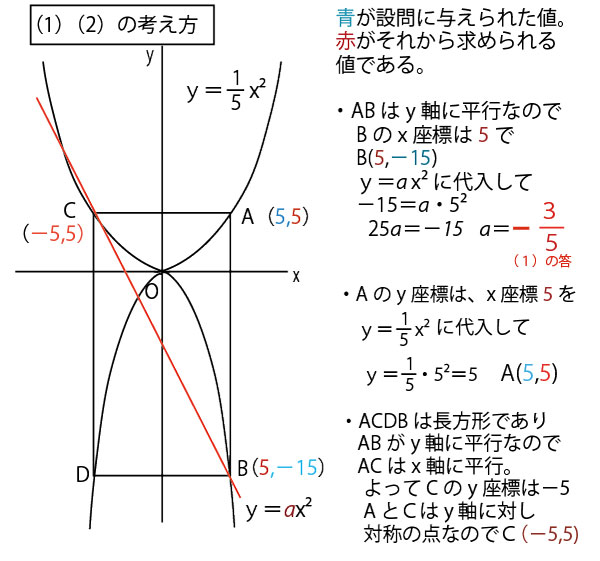
BCは、C（－５,5)、D（5,－15）を通るので、式をｙ＝mx+nとすると
(m,nとしたのは、上記のa～Ｄの記号と混同しないためです。混同しないようでしたら、ｙ＝ax+bとしてもいいです。）
5=－5m＋n…
－15＝5m＋n…
－より
10ｍ＝－20　ｍ＝－2
に代入して　５＝ー５×（－2）＋ｎ　　　ｎ＝５－10＝－５
よって点Ｂ、Ｃを通る直線の式はｙ＝－2m－5（（2）の答）

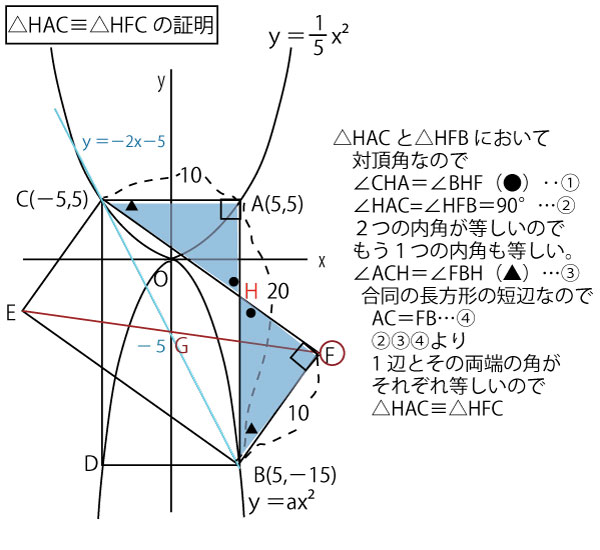
（3）
求めるべきEFを図に描画し、わかっていることを書き込んでみる。

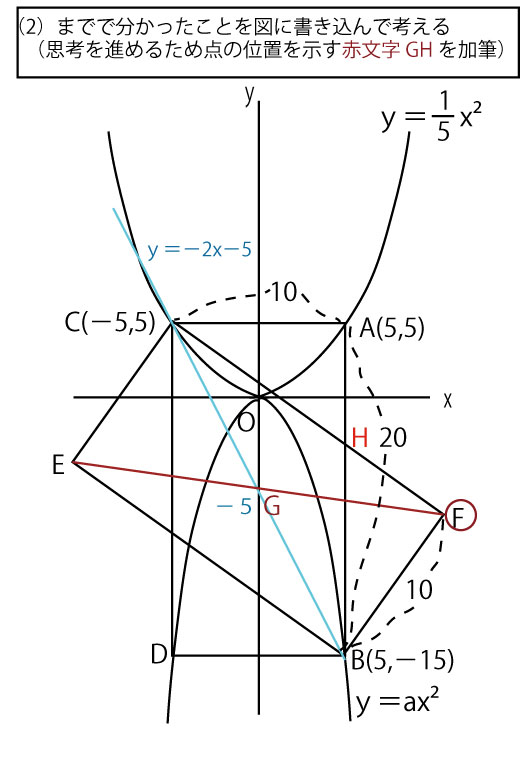
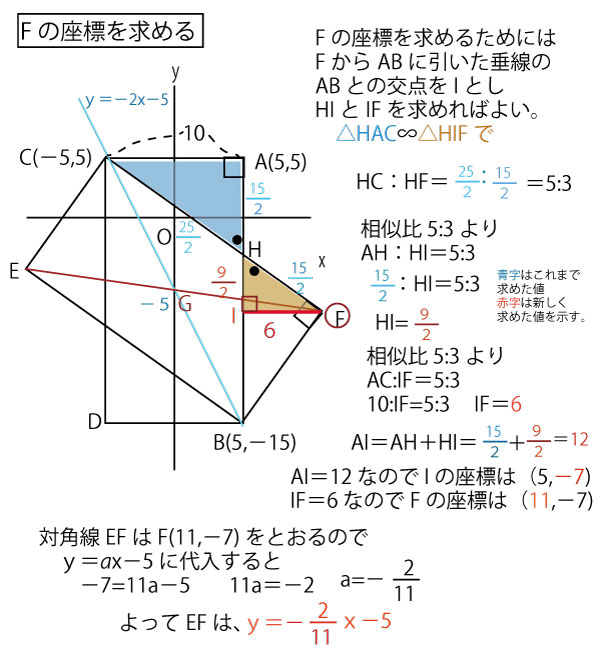
長方形の対角線は互いの中点で交わる。斜めの長方形ECFBで(2)で求めた対角線CBの中点GはＣ（－5,5)、B(5,－15)の中点なのでＧ（0,－5)であり、y軸上の点である。求めるべき長方形ＥＣＦＢのもう１つの対角線なので、この中点Ｇで交わる。つまりＥＦはＧ（0、－5)を通り、y切片－5の一次関数である。
EFはｙ＝ax−5とおくことができる。

ＥかＦの座標を求めることができ、その座標を代入すればaを求めることができる。
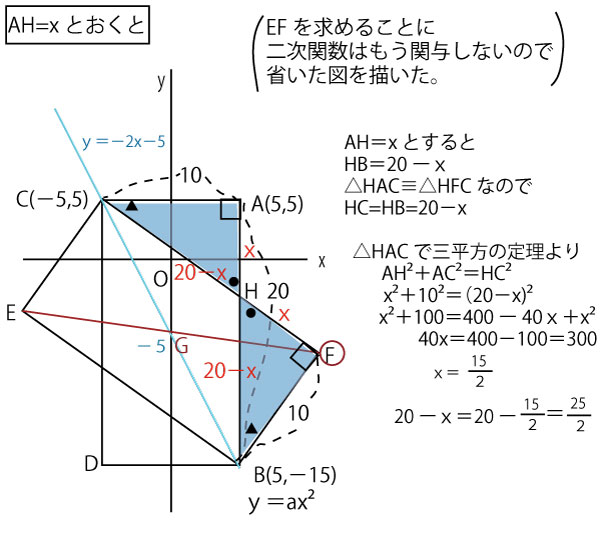
Ｆに注目すると、Ｆをすぐには求めることはできないが、ＣＦとＡＢの交点をＨとおき、Ｈを頂点に含む直角三角形△ＨＡＣや△ＨＦＢに注目し、三平方の定理を使うと、ＡＢ＝20、ＣＡ＝BF＝10の値がわかっているので求めることができそうである。