2022年千葉県公立高校入試「数学」第3問（図形の証明）問題、解答、解説（配点16点）

2022年7月　予備校講師・船橋市議　朝倉幹晴

2022年2月に実施された千葉県公立高校入試「数学」第3問（図形の証明）（計16点）の解答・解説を作成しました。このページ末尾で「２」を押しますと、解答・解説のページに飛びます。また千葉県教育委員会が発表した正答率・無答率も付記しました。学習や入試対策にご活用ください。

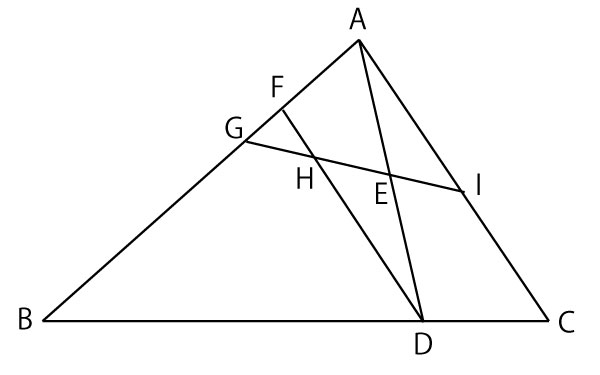
下の図のように、△ABCがあり、辺BC上にBD：DC＝3:1となる点Dをとる。線分ADの中点をEとし、点Dを通り、辺ACに平行な直線と辺ABとの交点をFとする。また、線分BF上に2点B、Fとは異なる点Gをとり、直線GEと線分DF、辺ACとの交点をそれぞれH、Iとする。このとき、次の（1）～（3）の問いに答えなさい。（計16点）

（1）AI＝DHであることを下のにしたがって証明するとき、（a)(b)に入る最も適当なものを、選択肢のア～エのうちから１つずつ選び、符号で答えなさい。また、（c）に入る最も適当なことばを書きなさい。（完答で5点）
                                                                                                                                                                                                                                                                                （正答率78.6%、無答率0.1%)

選択肢　ア△AEI　イ△ABD　ウ△AFD　エ△DEH

（2）（1）のにしたがって、AI＝DHであることを証明しなさい。（6点）（正答率28.2％（6点）、部分点（3点配点）（8.3%)、無答率27.4%)

（3）のとき、△AEIと四角形BDHGの面積の比を、最も簡単な整数の比で表しなさい。（5点）  （正答率5.5%、無答率39.1%)

[next_p]