2023年大学入試共通テスト数学IA第2問［１］（15点）問題・解答・解説

【解説】

（1）

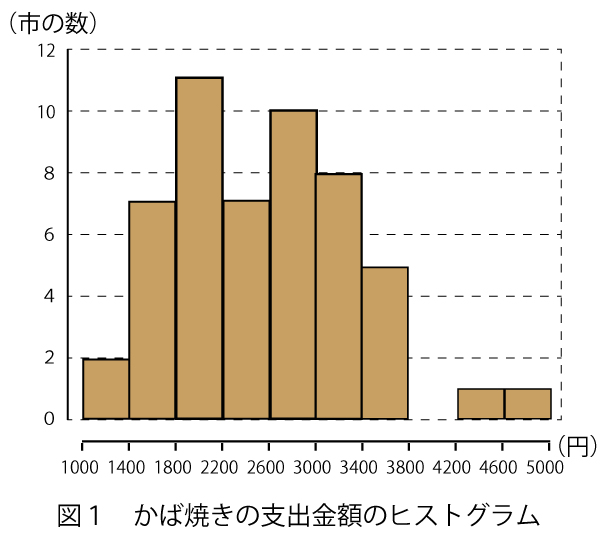
各階級の度数と小さい値からの累積度数を図１の下に記すと以下のようになる。

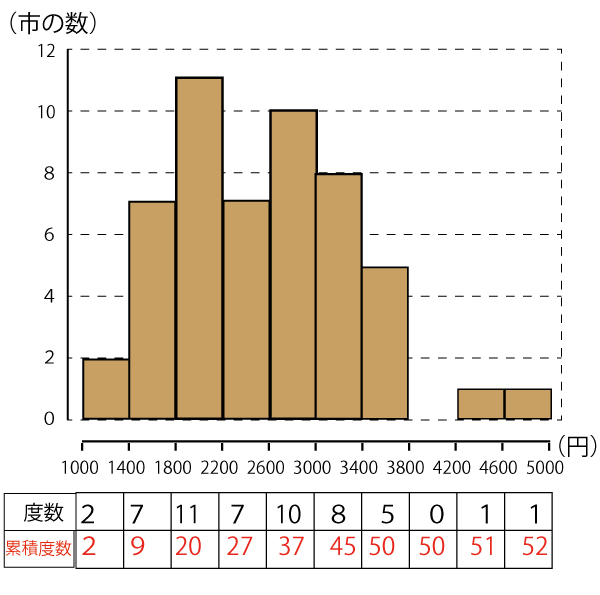
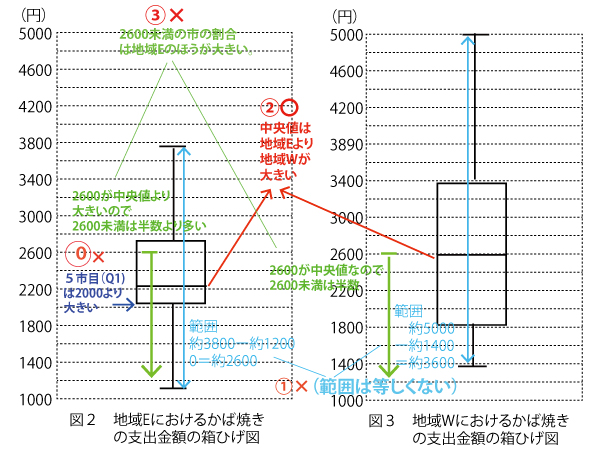
52市なので、中央値（Q₂)は小さいほうかから26番目と27番目の平均値、つまり2600以上3000未満の階級の中にある。
そしてQ_１は値が小さい26市の中央値なので、13番目と14番目の平均値となる。つまり1800以上2200未満の階級にある。ア_{（2点）
（2点）}

Q_{3は値が大きい26市の中央値なので、26＋13＝39番目と26＋14＝40番目の平均値となる。3000以上3400未満の階級にある。イ（2点）}

四分位範囲はQ₃－Q₁なので3000以上3400未満の値から、1800以上2200未満の値を引いたものになる。
差が最大の場合、3400未満ー1800＝1600未満。
差が最小の場合は、3000ー2200未満＝800以上。
よって800以上1600未満。ウ（2点）

（2）
（i）地域Eは19市なので、中央値（Q2)は小さいほうから10市目である。この中央値より値が小さい１～９市目の中央値がQ1なのでQ₁は５市目である。

図の中で説明したように、正解はエ（3点）

（ii）分散の定義より（3点）

（3）相関係数とは以下のように計算される。

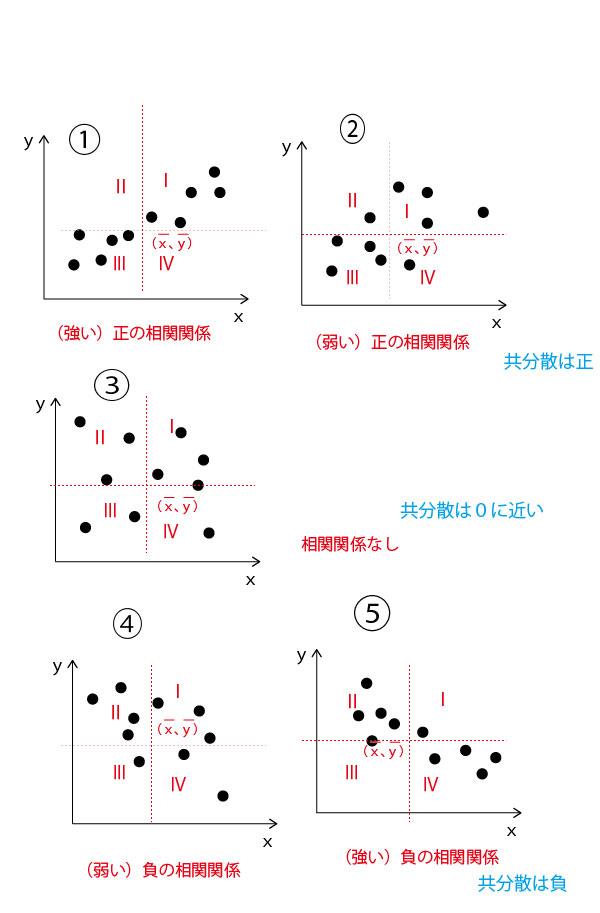
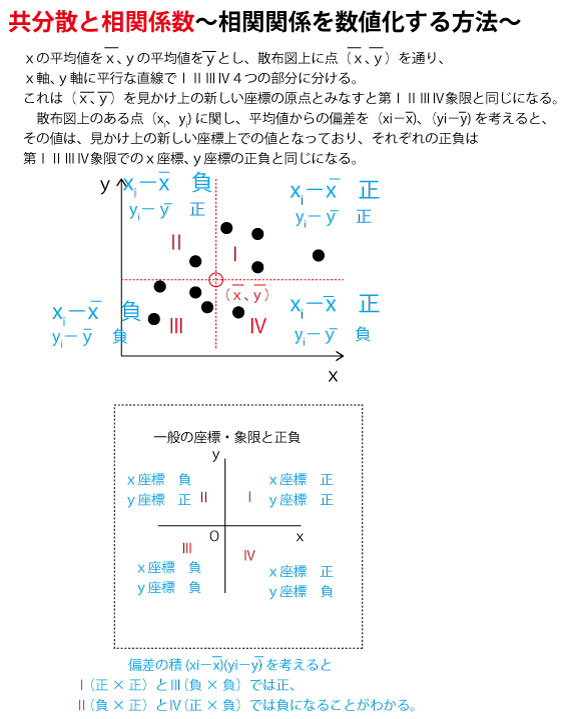
相関係数＝共分散÷やきとり支出の標準偏差÷かばやき支出の標準偏差
＝124000÷590÷570＝0.368…≒0.37。カ（3点）

 

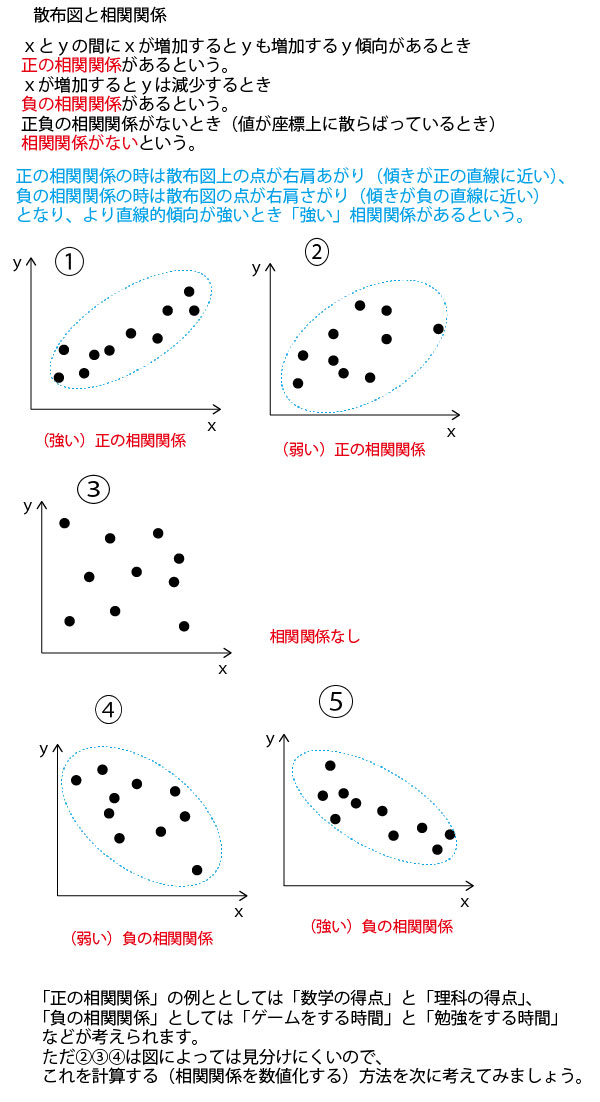
よって地域E（東日本）では、やきとりの支出金額とかばやきの支出金額の間には、弱い正の相関関係がある。つまりやきとりが好きな地域は、かばやきも好きである傾向があるという結果となっている。

↓以下は基礎知識のまとめです

★【中学（中１「資料の整理」）】分野のまとめ

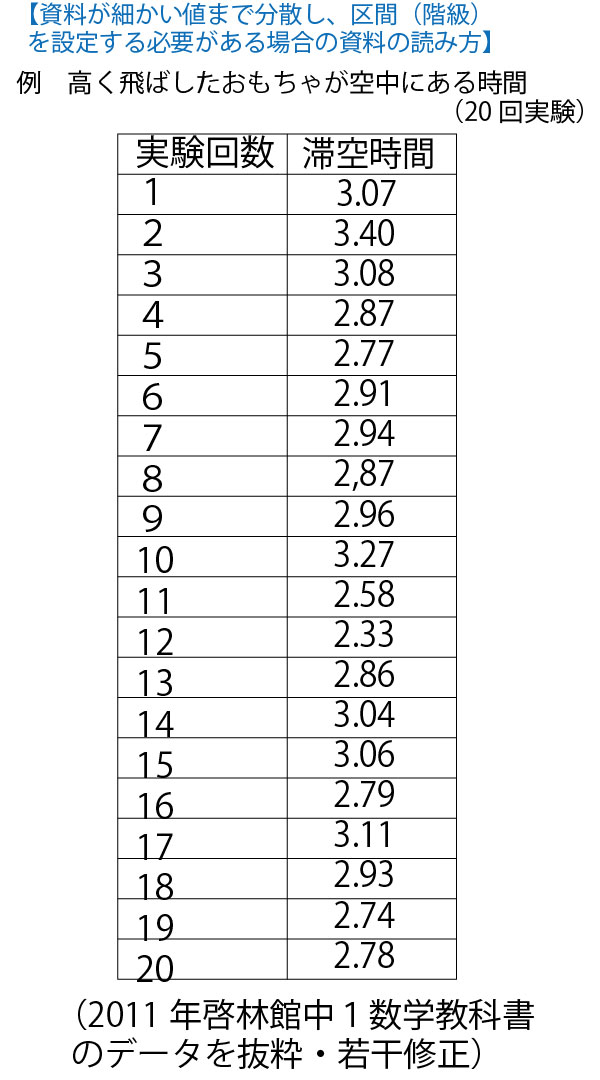
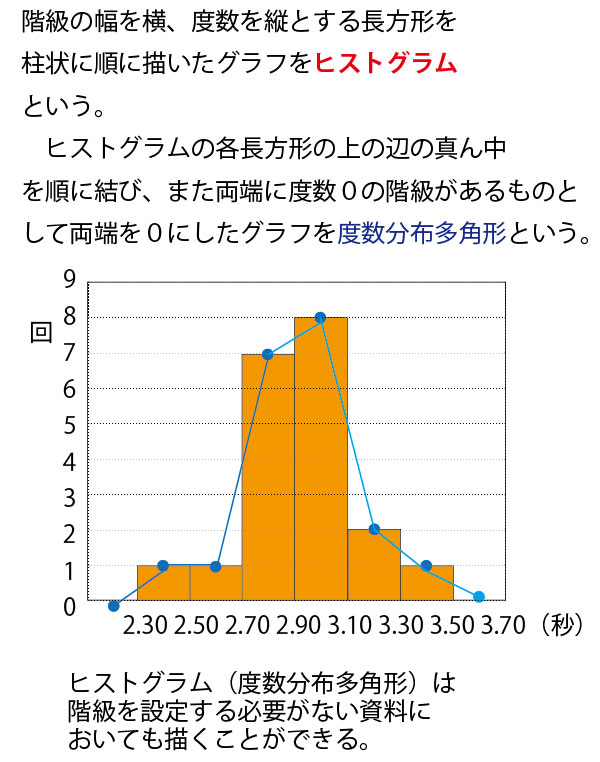
★高校数Ⅰ（データの分析）分野のまとめ。

中学１年で学ぶ「資料の整理」の発展編であり、この学問分野を統計学という。

具体例として、数学の小テスト（10点満点）の平均点がいずれも5点が分布が異なる30人の７クラス（１組～7組）を例に考えていこう。

 

 

 

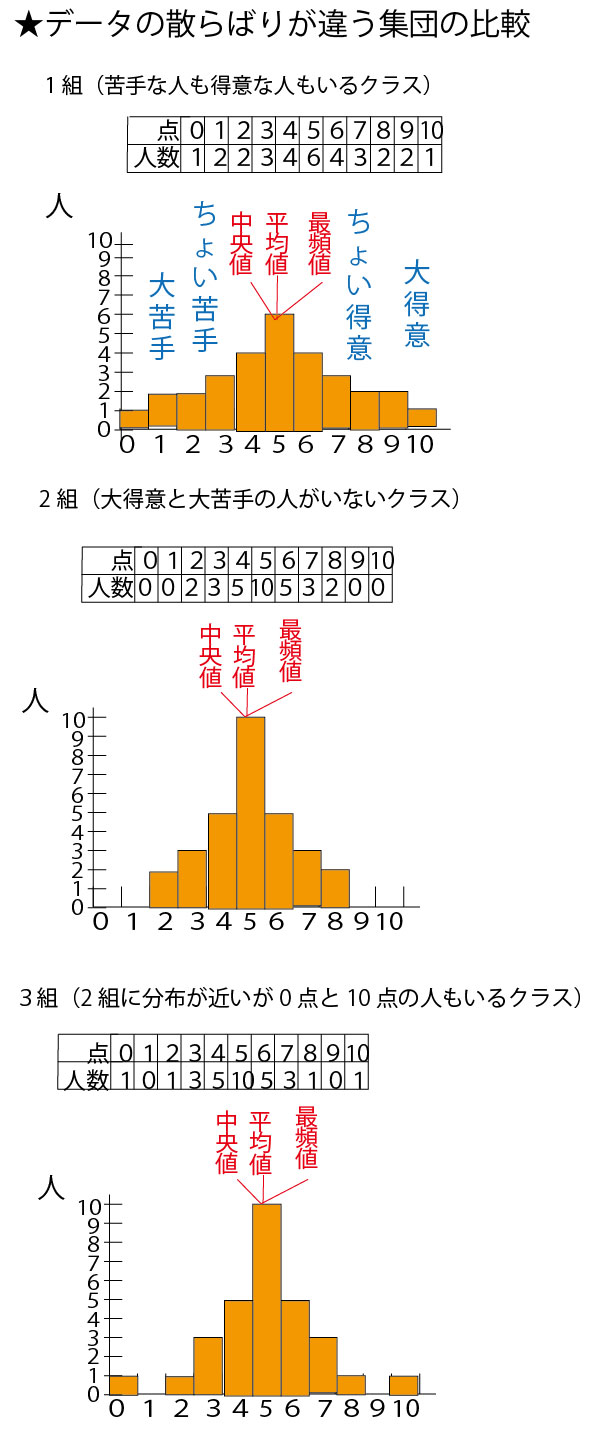
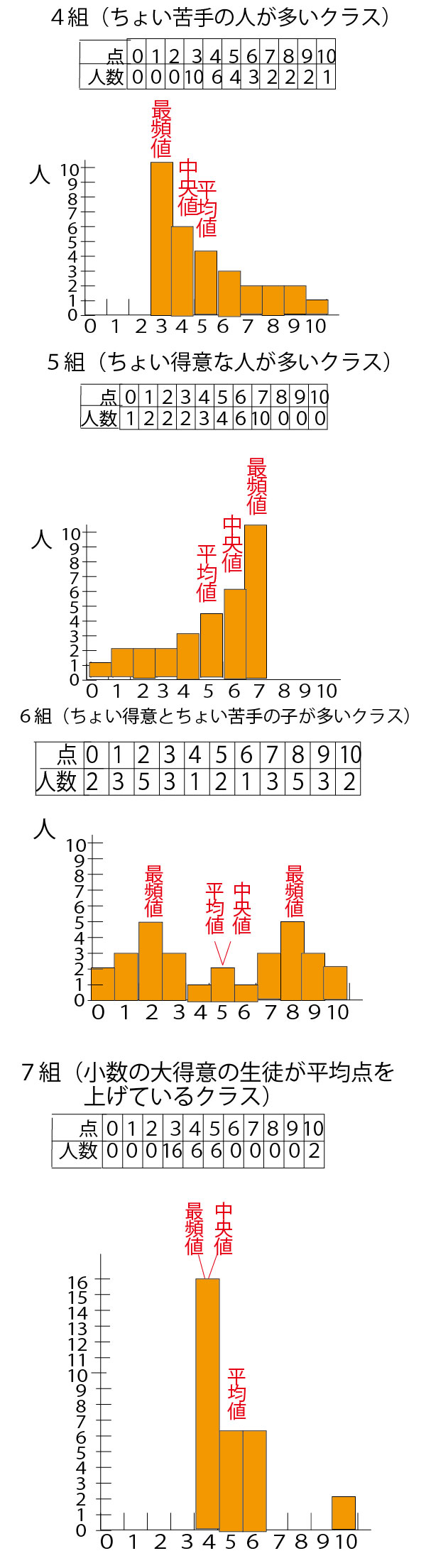
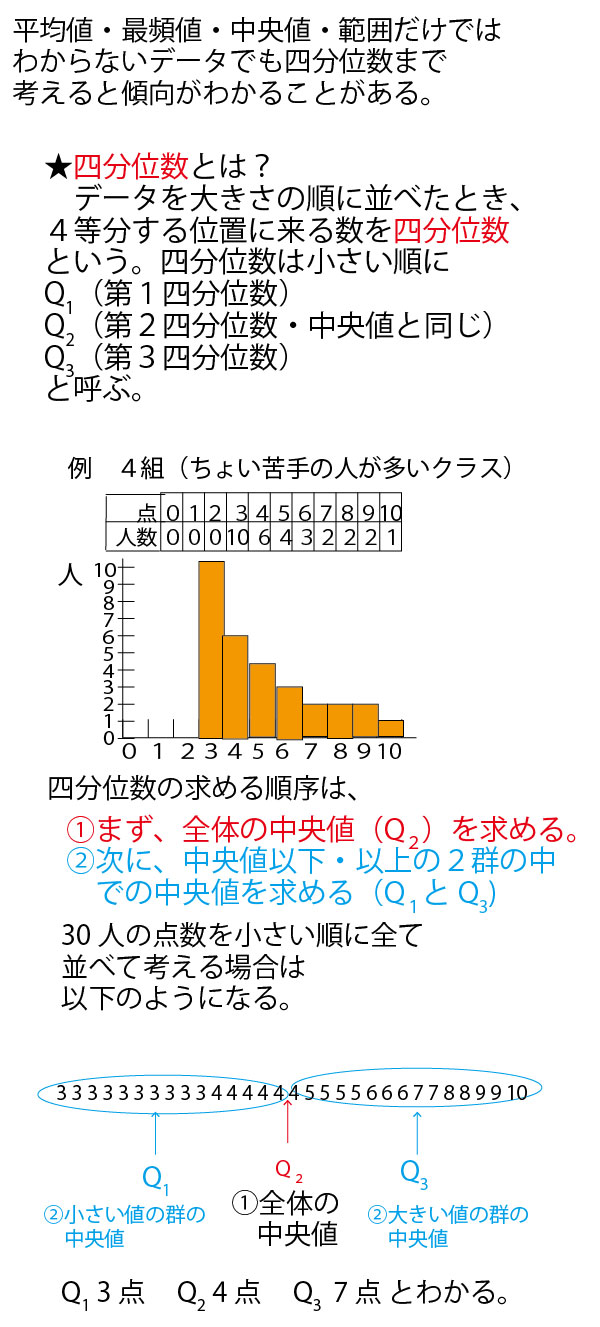
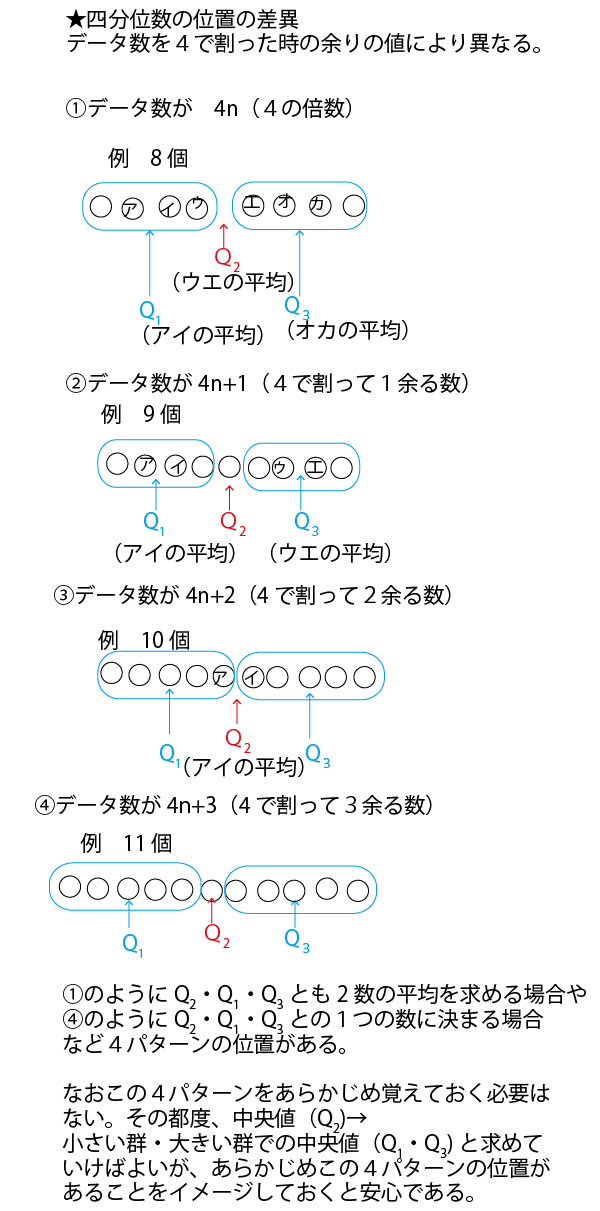
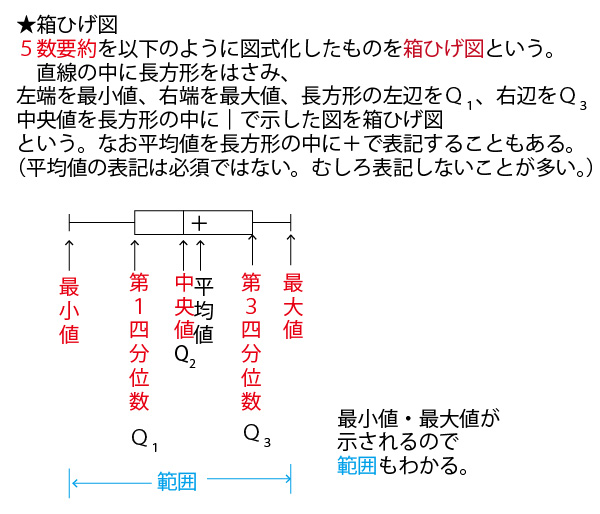
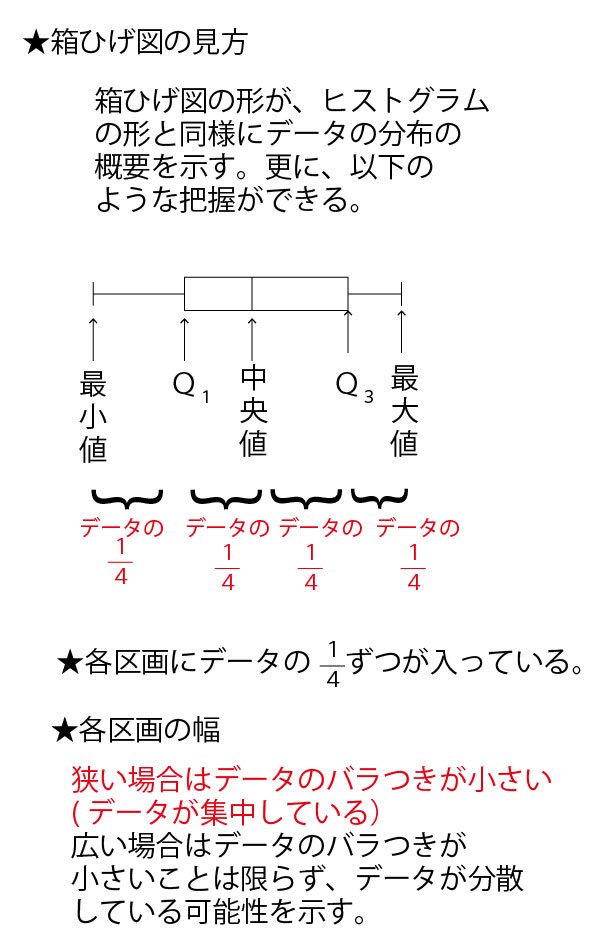
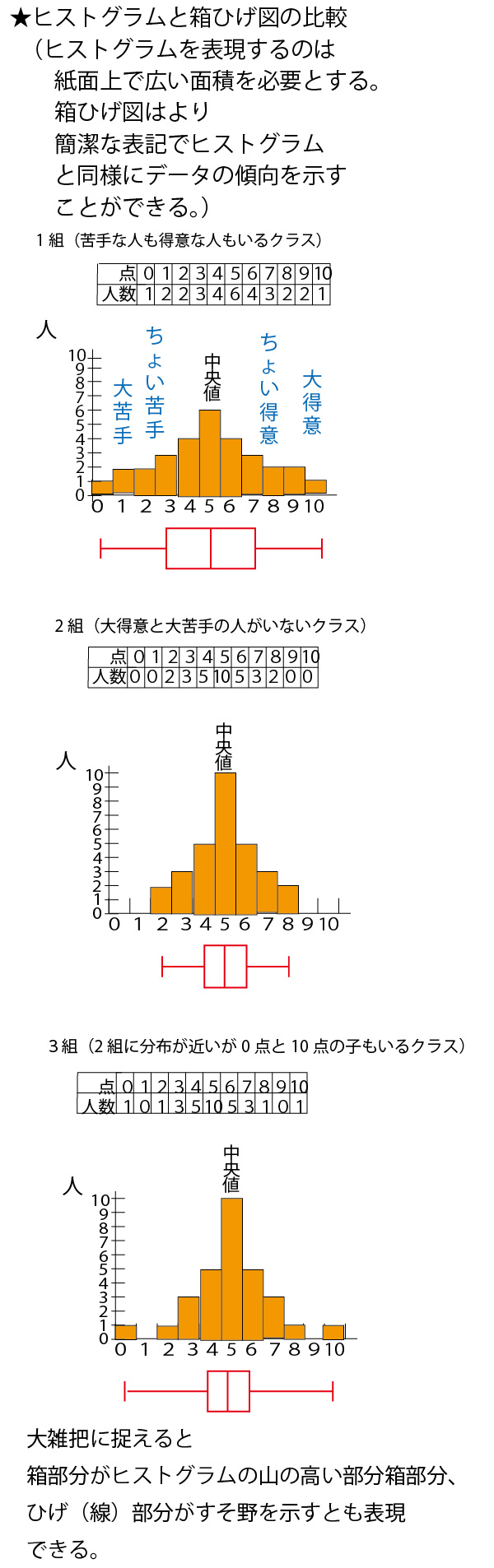
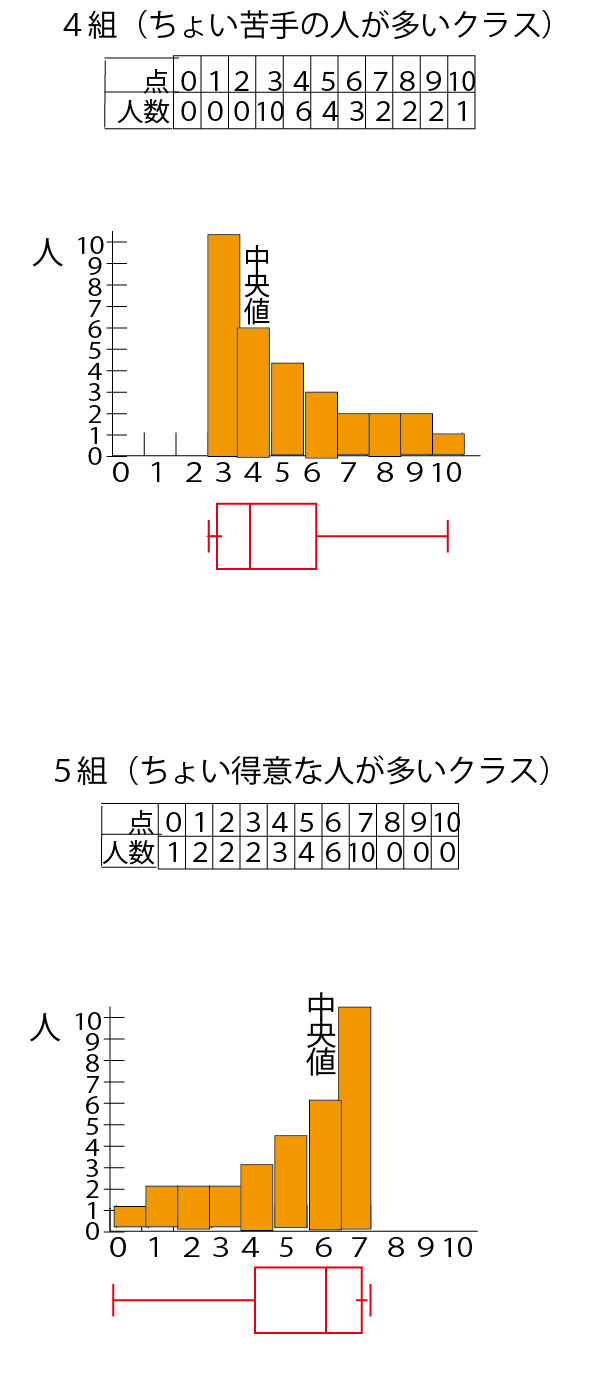
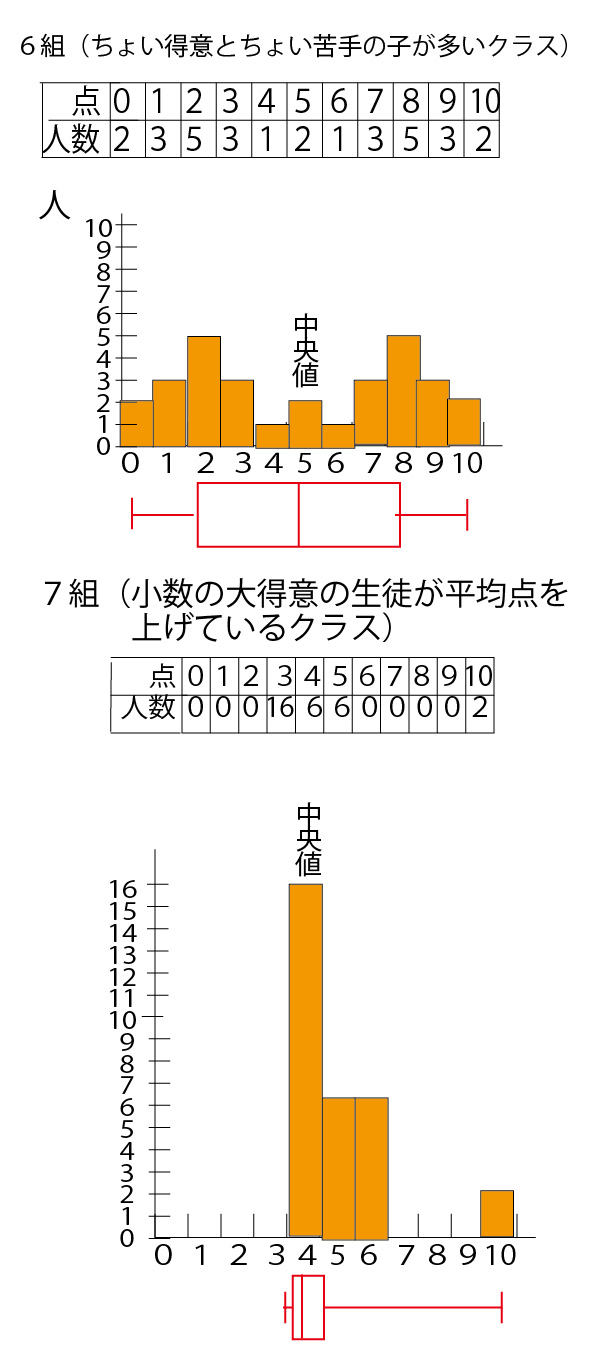
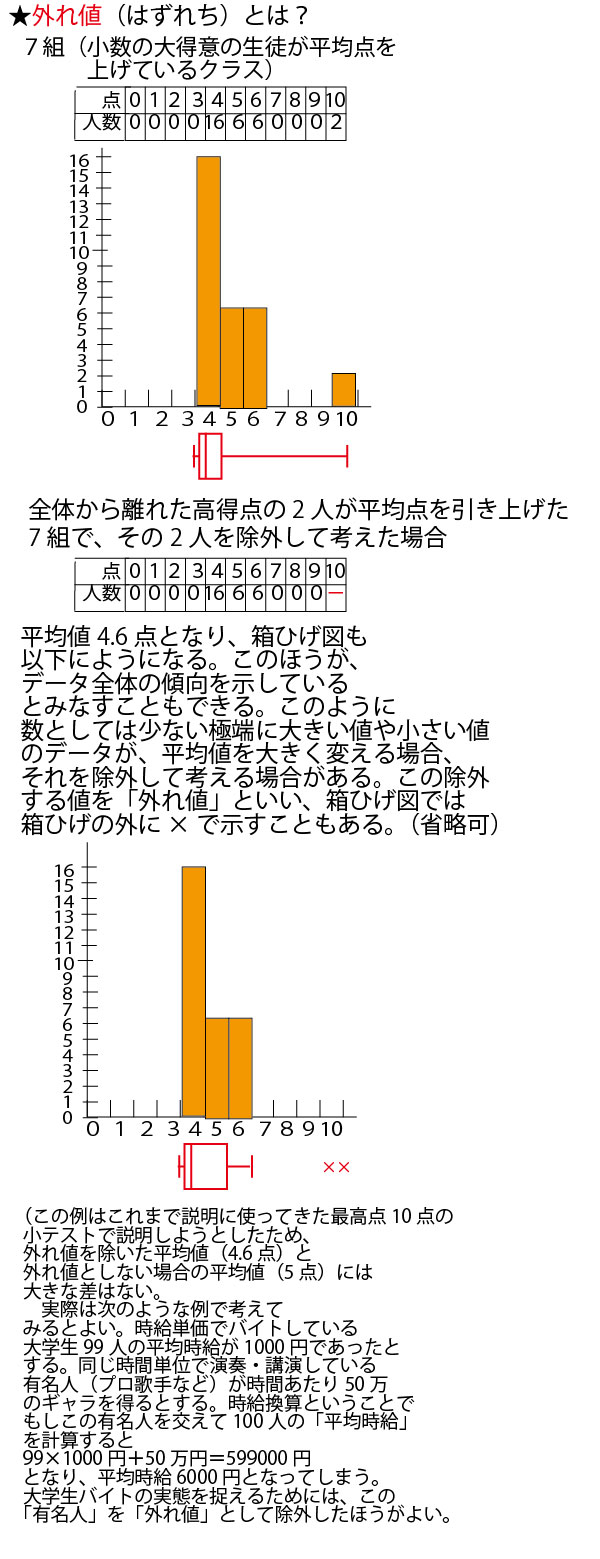
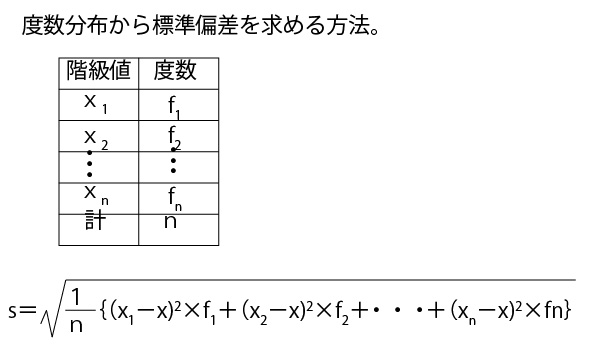
分散・標準偏差に関しては、最初に考えるのは30人クラスでは大きすぎて考えにくいので、まずは、平均点がいずれも5点となる5人組の５班（１班～５班）を例に考えていこう。