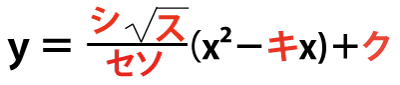2023年大学入試共通テスト「数学１A」第2問［２］（15点）問題・解答・解説
asakura
2023年12月13日 予備校講師・船橋市議 朝倉幹晴
2023年大学入試共通テスト「数学１A」第2問［2］（配点15点）の解答・解説を作成しましたので、ご活用ください。問題文の最後の所でページ番号「２」をクリックすると解答・解説に飛びます。
入試問題は黒印刷ですが、せっかくの画面上ですので、図はカラーにしました。
（シュートをしている選手の背の高いプロ選手は、スラムダンクの桜木花道をイメージして赤髪にしました。（桜木花道は高校生ですが、将来プロになったと仮定します。）
2023年大学入試共通テスト「数学１A」第2問［２］（15点）
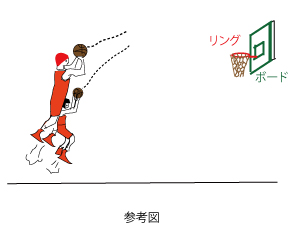
[2]太郎さんと花子さんは、バスケットボールのプロ選手の中には、リングと同じ高さでシュートを打てる人がいることを知り、シュートを打つ高さによってボールの軌道がどう変わるかについて考えている。
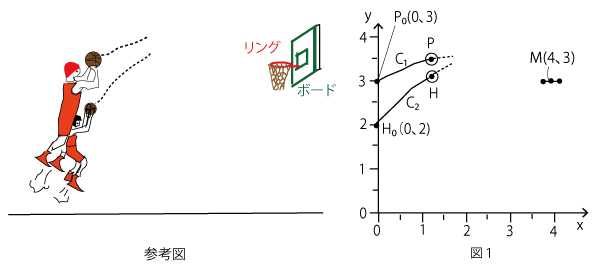
二人は、図１のように座標軸が定められた平面上に、プロ選手と花子さんがシュートを打つ様子を真横からみた図をかき、ボールがリングに入った場合について、後の仮定を設定して考えることにした。長さの単位はメートルであるが、以下では省略する。
仮定
・平面上では、ボールを直径0.2の円とする。
・リングを真横から見たときの左端を点Ａ(3.8、3)、右橋を点B（4.2、3)とし、リングの太さは無視する。
・ボールがリングや他のものに当たらずに上からリングを通り、かつ、ボールの中心がABの中点M（4、3)を通る場合を考える。ただし、ボールがリングに当たるとは、ボールの中心とAまたはBとの距離がo.1以下になることとする。
・プロ選手がシュートを打つ場合のボールの中心を点Pとし、Pは、はじめに
点Ｐ0(0、3)にあるものとする。また、P0、Ｍを通る、上に凸の放物線をC1とし、ＰはC1上を動くものとする。
・花子さんがシュートを打つ場合のボールの中心を点Ｈとし、Ｈは、はじめに点Ｈo(0、2)にあるものとする。また、H0、Mを通る、上に凸の放物線をC2とし、HはC2上を動くものとする。
・放物線C1やC2に対して、頂点のｙ座標を「シュートの高さ」とし、頂点のｘ座標を「ボールが最も高くなるときの地上の位置」とする。
（1）放物線C1の方程式におけるx2の係数をaとする。放物線Ｃ1の方程式は
y=ax2－キax＋ク（キクあわせて3点）
と表すことができる。また、プロ選手の「シュートの高さ」は
－ケa+コ（ケコあわせて3点）
である。
放物線Ｃ2の方程式におけるx2の係数をｐとする。放物線C2の方程式は
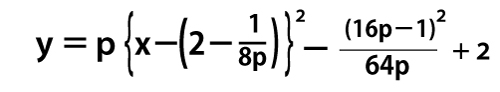
と表すことができる。
プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」の比較の記述として、次ののうち、正しいものはサ（3点）である。
サの解答群
プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」は、つねに一致する。
プロ選手の「ボールが最も高くなるときの地上の位置」の方が、つねにMのＸ座標に近い。
花子さんの「ボールが最も高くなるときの地上の位置」の方が、つねにMのｘ座標に近い。
プロ選手の「ボールが最も高くなるときの地上の位置」の方がMのx座標に近いときもあれば、花子さんの「ボールが最も高くなるときの地上の位置」の方がＭのｘ座標に近いときもある。
（2）二人は、ボールがリングすれすれを通る場合のプロ選手と花子さんの「シュートの高さ」について次のように話している。
太郎：例えば、プロ選手のボールがリングに当たらないようにするには、Pがリングの左端Aのどのくらい上を通れば良いのかな。
花子：Aの真上の点でPが通る点Dを、線分DMがAを中心とする半径0.1の円と接するようにとって考えてみたらどうかな。
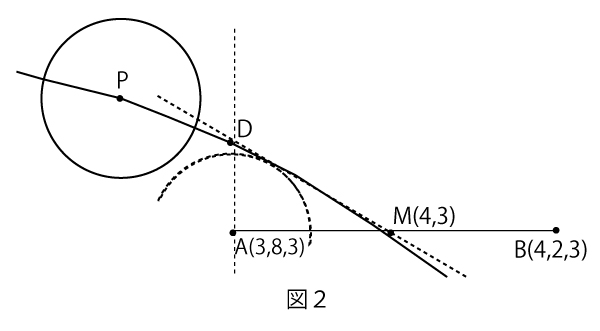
太郎：なるほど、Pの軌道は上に凸の放物線で山なりだから、その場合、図２のように、PはDを通った後で線分DMより上側を通るので、ボールはリングに当たらないね。花子さんの場合も、HがこのDを通れば、ボールはリングに当たらないね。
花子：放物線C1とC2がDを通る場合でプロ選手と私の「シュートの高さ」を比べてみようよ。
図２のように、Mを通る直線ℓが、Aを中心とする半径0.1の円に直線ABの上側で接しているとする。また、Aを通り直線ABに垂直な直線を引き、ℓとの交点をDとする。このとき である。
よって、放物線C1がDを通るとき、C1の方程式は、
（シスセソ合わせて3点）
となる。
また、放物線C2がDを通るとき、（1）で考えられたC2の方程式を用いると、花子さんの「シュートの高さ」は約3.4と求められる。
以上のことから、放物線C1とC2がDを通るときプロ選手と花子さんの「シュートの高さ」を比べると、タの「シュートの高さ」の方が大きく、その差はボールチである。（タチあわせて3点）
なお、
である。
[next_p]
