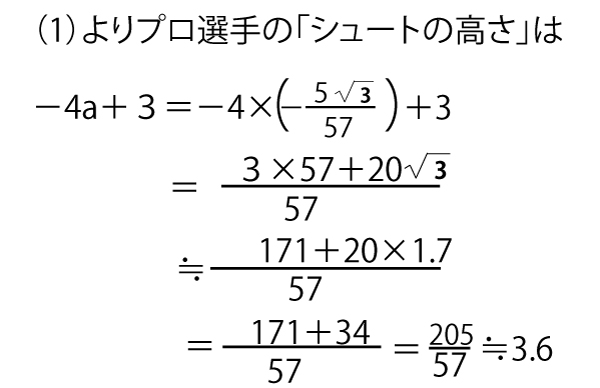2023年大学入試共通テスト「数学1A」第2問[2](15点)問題・解答・解説
【解説】
キク・ケコ
C1はPo(0、3)とM(4、3)を通り、PoとMのy座標(高さ)は3で同じなので、放物線の軸は、P0とMの中点を通るx=2と考えられる。頂点を
(2、q)とする、つまりシュートの高さをqとすると
y=a(x-2)2+q
y=ax2−4ax+4a+q
y切片は3なので
y=ax2−4ax+3(キク答、合わせて3点)
4a+q=3なので
q=-4a+3(ケコ答、合わせて3点)
サ
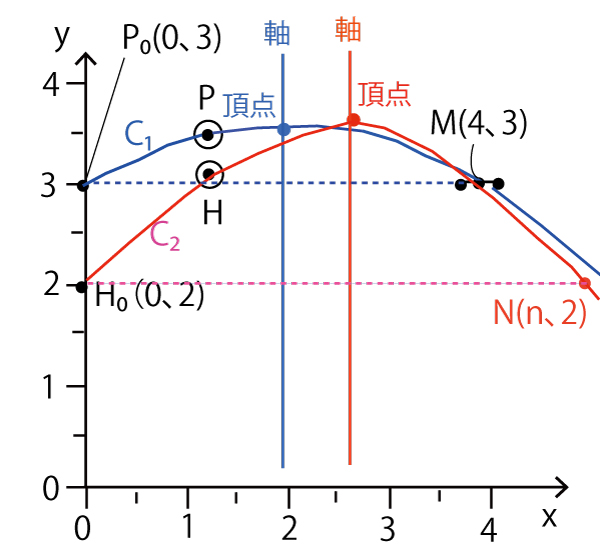
実際のバスケットボールでは、放物線を描いてゴールに入ったボールは、ゴールゴールから垂直に落ちることになるが、理論上、その放物線がそのまま延長してゴールの右下まで放物線が続くと考える。すると次のように、プロ選手の放物線
C1を青線のように、花子さんの放物線C2を赤線のように描くことができる。
放物線は軸に対して線対称である。
放物線C1について、PO(0、3)と同じy座標(高さ)の点M(4、3)を赤点線のように結ぶと放物線の軸と直交し、軸は線分PONの中点、つまりx座標2を通るので軸はx=2となる。
同様に、放物線C2について、HO(0、2)とy座標(高さ)は同じとなる点N(n、2)を考えると、軸は線分H0Nの中点を通る。図より、N(n、2)のx座標は、M(4、3)のx座標より大きいのでn>4。よってHONの中点、軸のx座標は2より大きい。したがって、
花子さんの「ボールが最も高くなるとき(頂点(軸))の地上の位置(x座標)」は、プロ選手の頂点(軸)のx座標2より大きく、つねにMのx座標4に近い。よって![]() (3点)
(3点)
(頂点のy座標(高さ)については、この条件だけではわからないので、![]()
は答ではない。)
C2の難しい方程式は無視して使わなくても解ける。このような共通テスト数学IAのレベルでは扱わない難しい式と、![]() の選択肢で選ぶことを求められている内容を比較し、「難しい方程式は、例として示したもので、解答には使用しないのではないか?」と予測し、別の角度の上記のような発想で考えることが大切である。
の選択肢で選ぶことを求められている内容を比較し、「難しい方程式は、例として示したもので、解答には使用しないのではないか?」と予測し、別の角度の上記のような発想で考えることが大切である。
シスセソ
「シュートの高さ」は,プロ選手が3.6、花子さんが3.4でプロ選手のほうが高く(タ![]() )、その差は0.2で直径にほぼ等しいので、ボール約1個分(チ
)、その差は0.2で直径にほぼ等しいので、ボール約1個分(チ![]() )
)
【総評】
バスケットボールにおけるプロと素人の差(身長差)の要素分析など題材は、身近なもので興味深い。
しかし、高校生の標準的な学力を問う問題としてはこの問2[2]は難しいし、時間内にすべて問題文を読み込めるのかが疑問である。問2[1]は解けてほしいが、問2[2]が出来が悪いのはあまり気にしなくてもよいと思う。
ただ、この形の出題が今年も続く場合のコツは以下の通りである。
1、問題文の中の式は設定、たとえば(1)の式や、(2)の図2の細かい数値は実は無視しても問題を解くことができる。多数の情報の中から問題を解くのに必要な計算のみを行うように短時間で判断して選ぶことが必要である。
2、同じく時間の節約の観点から、チがボール約1個分、2個分どうしで20cmの差のある形での選択を聞いているので、![]()
と書いてあるが、約1.7で計算し、計算時間を節約するのがよい。
↓以下は中学・高校の統計分野の基礎事項の総まとめです。
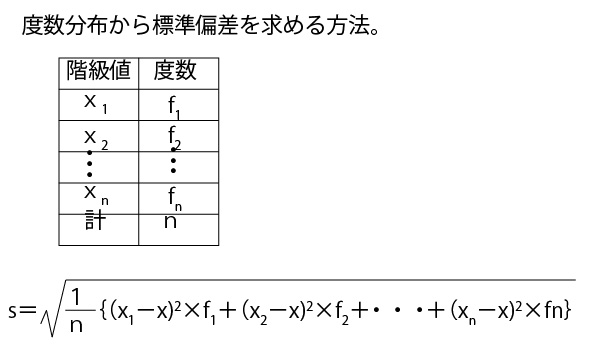
★【中学(中1「資料の整理」)】分野のまとめ

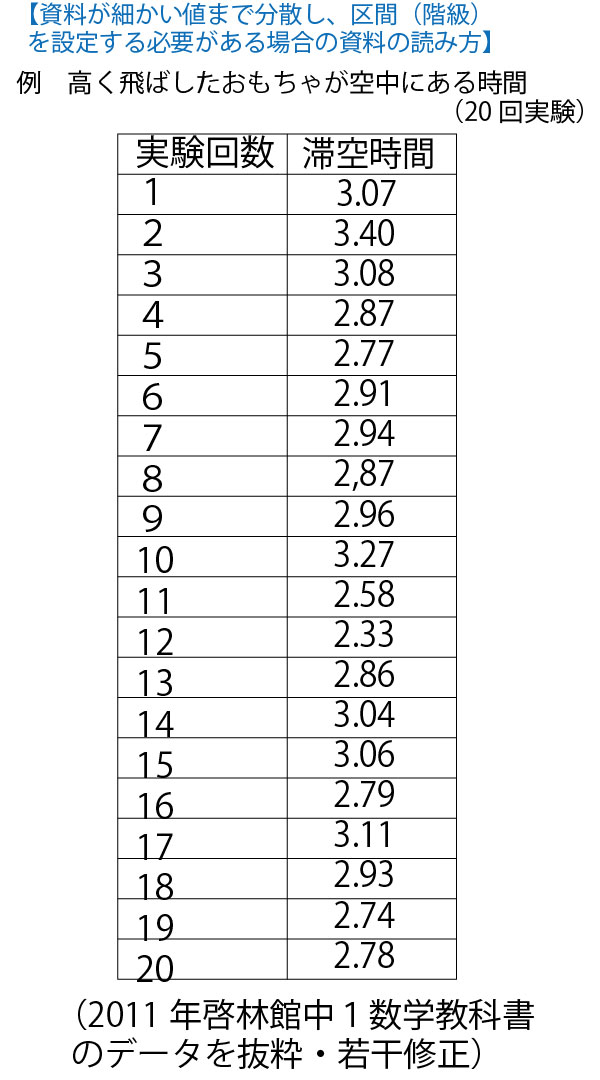

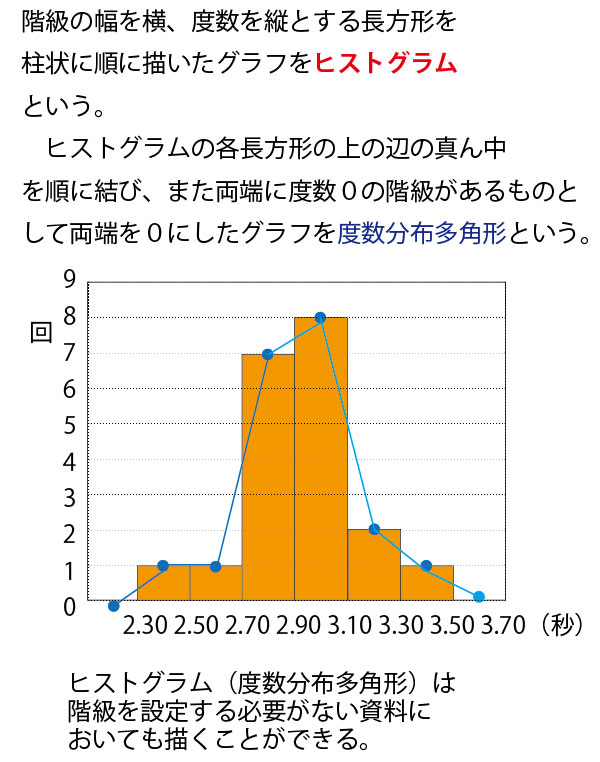
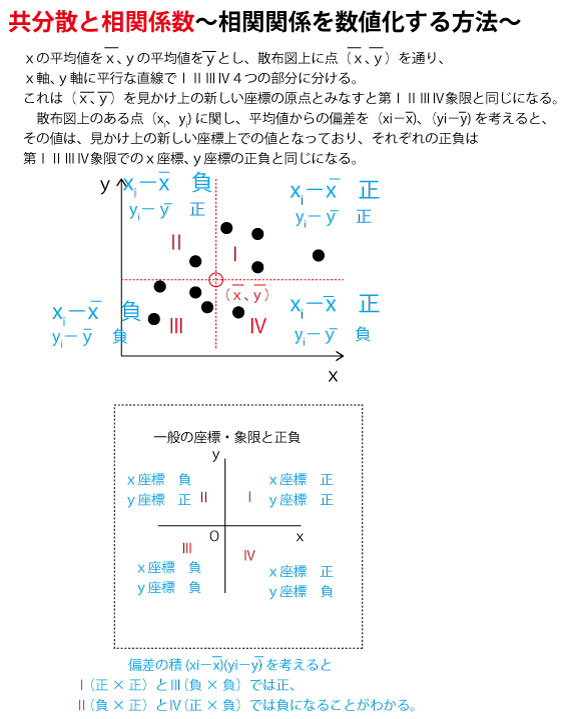
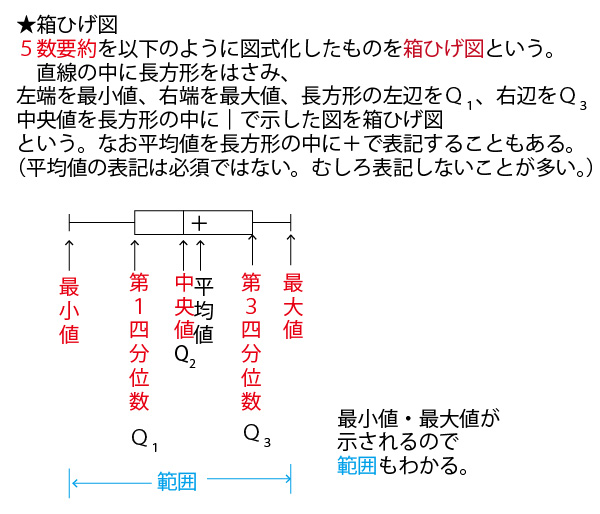
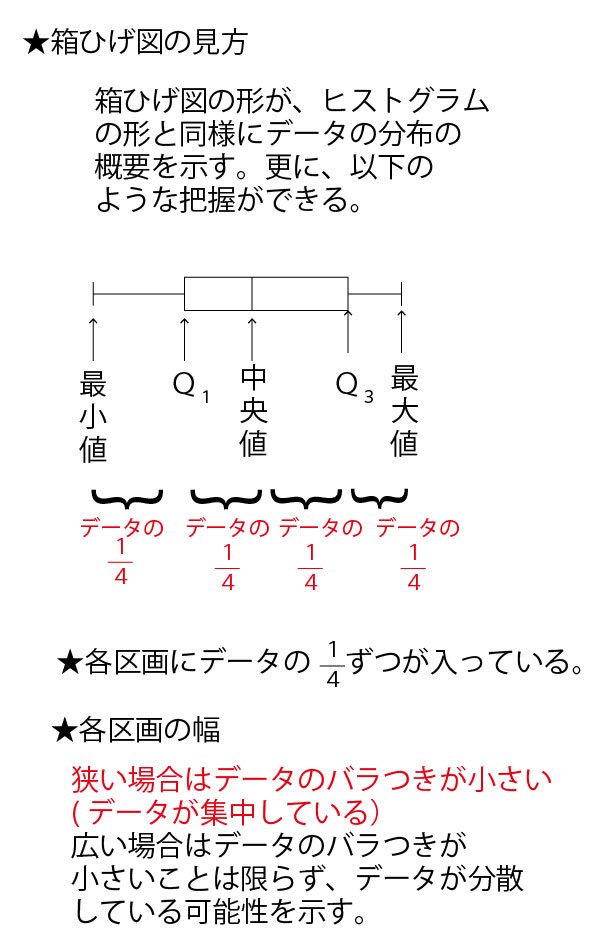
★高校数Ⅰ(データの分析)分野のまとめ。
中学1年で学ぶ「資料の整理」の発展編であり、この学問分野を統計学という。
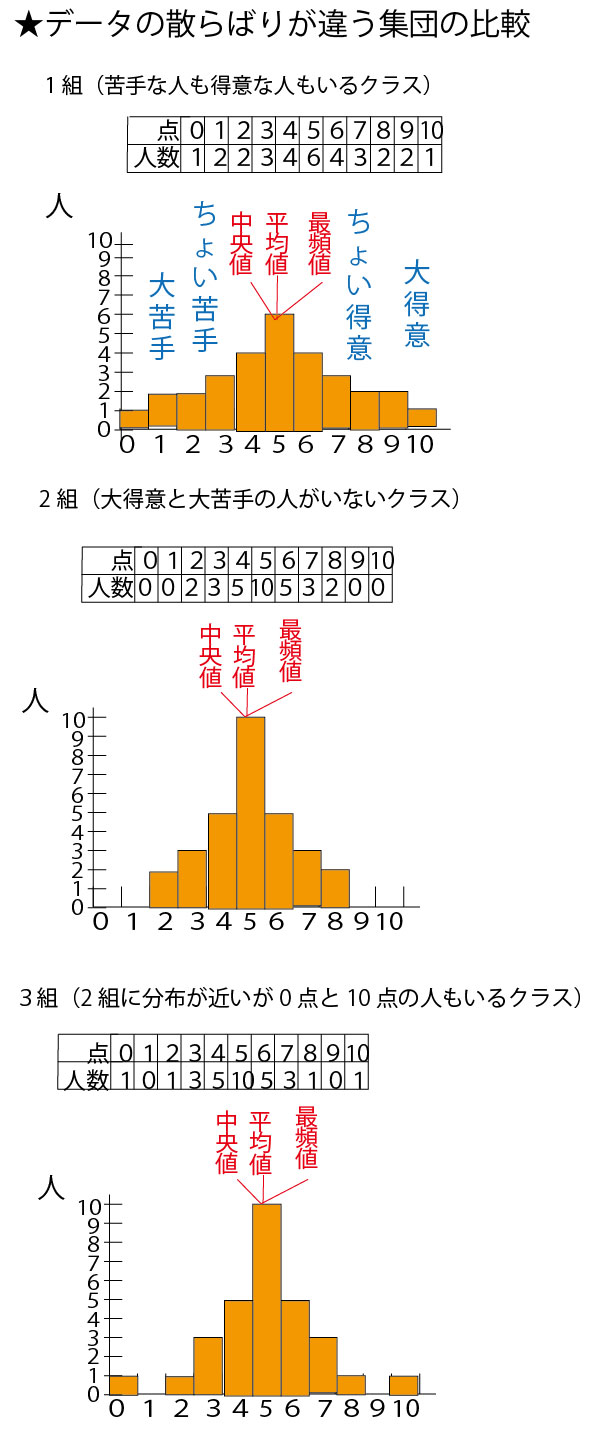
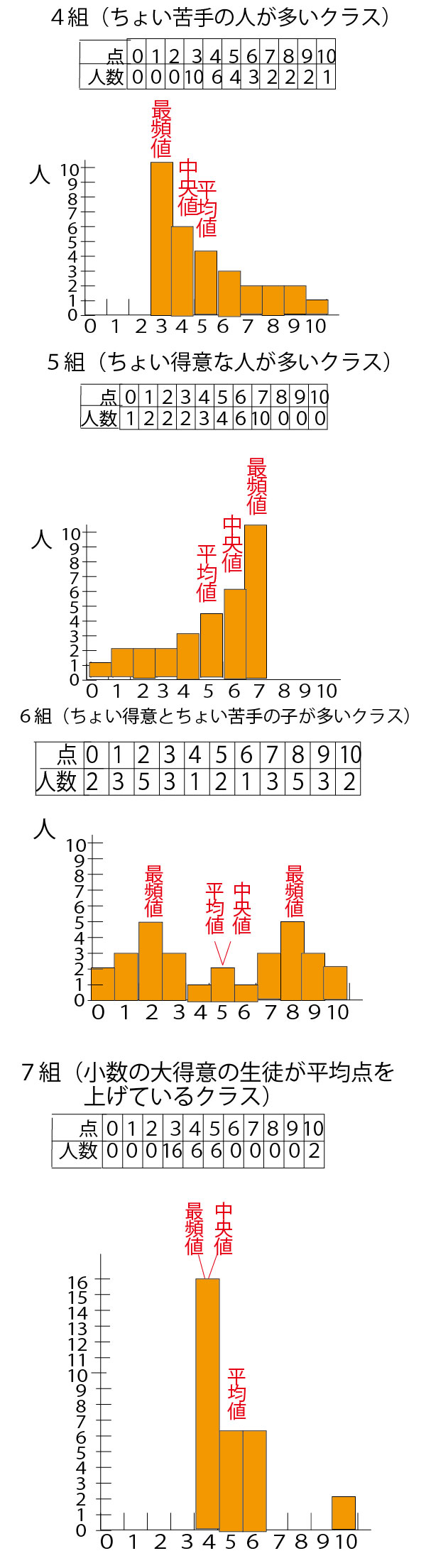
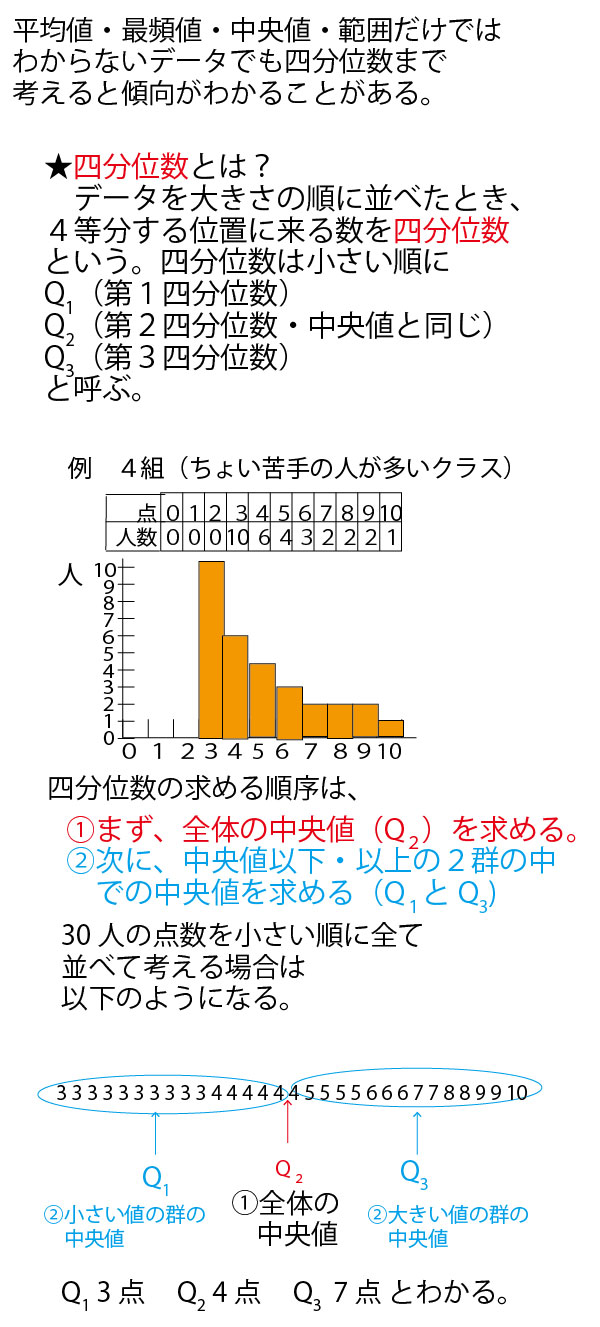
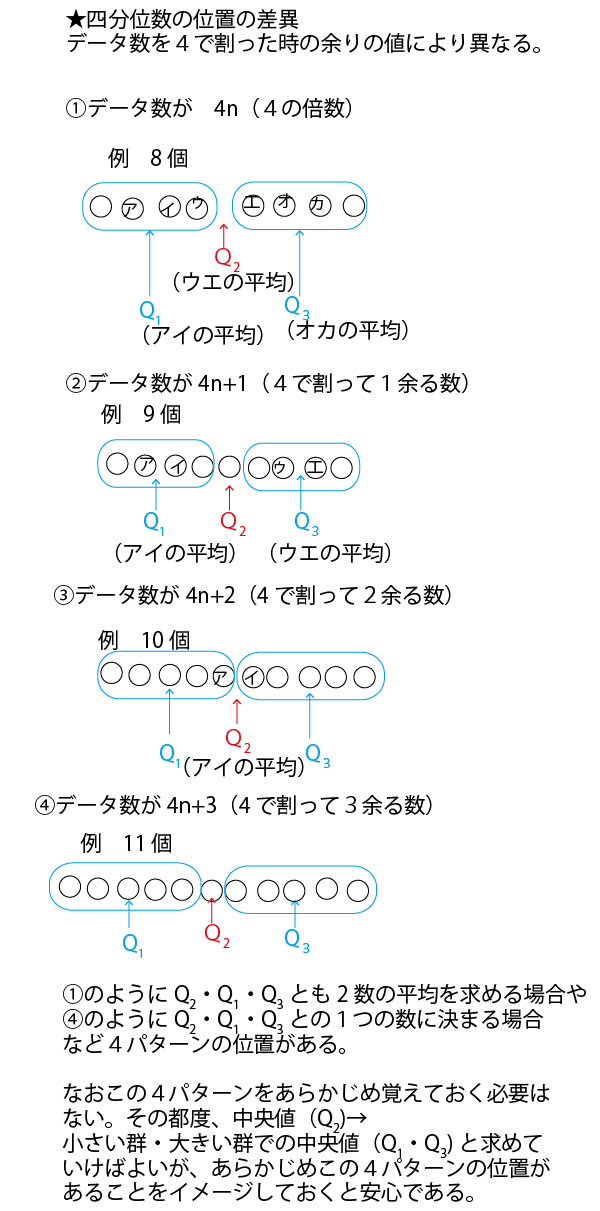
具体例として、数学の小テスト(10点満点)の平均点がいずれも5点が分布が異なる30人の7クラス(1組~7組)を例に考えていこう。






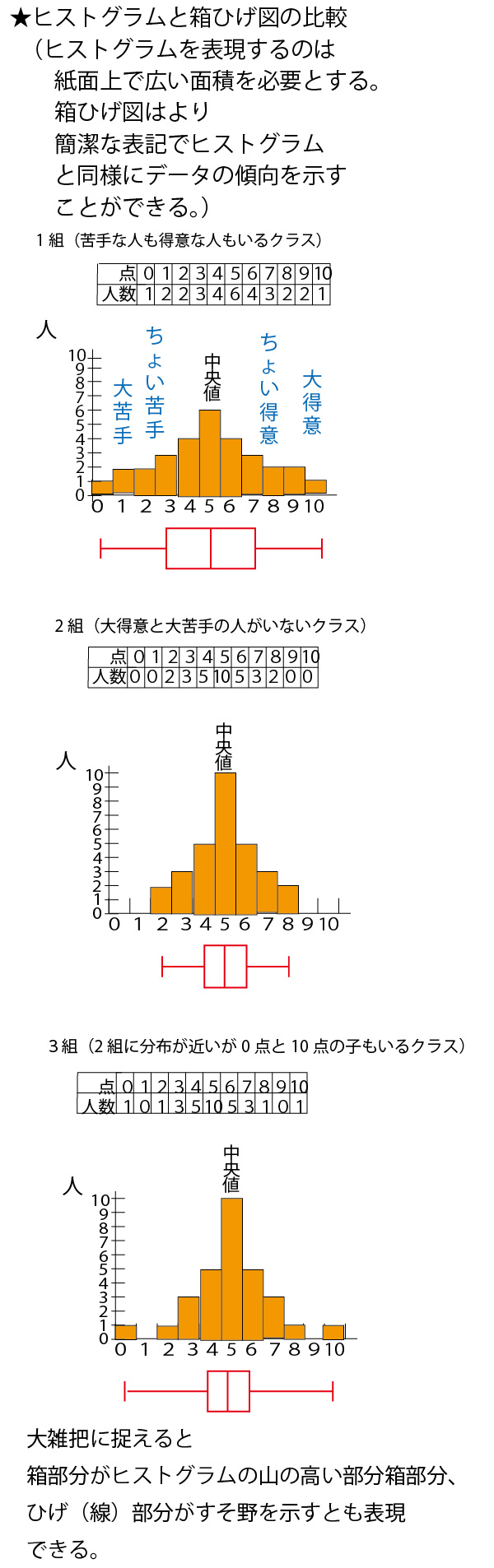
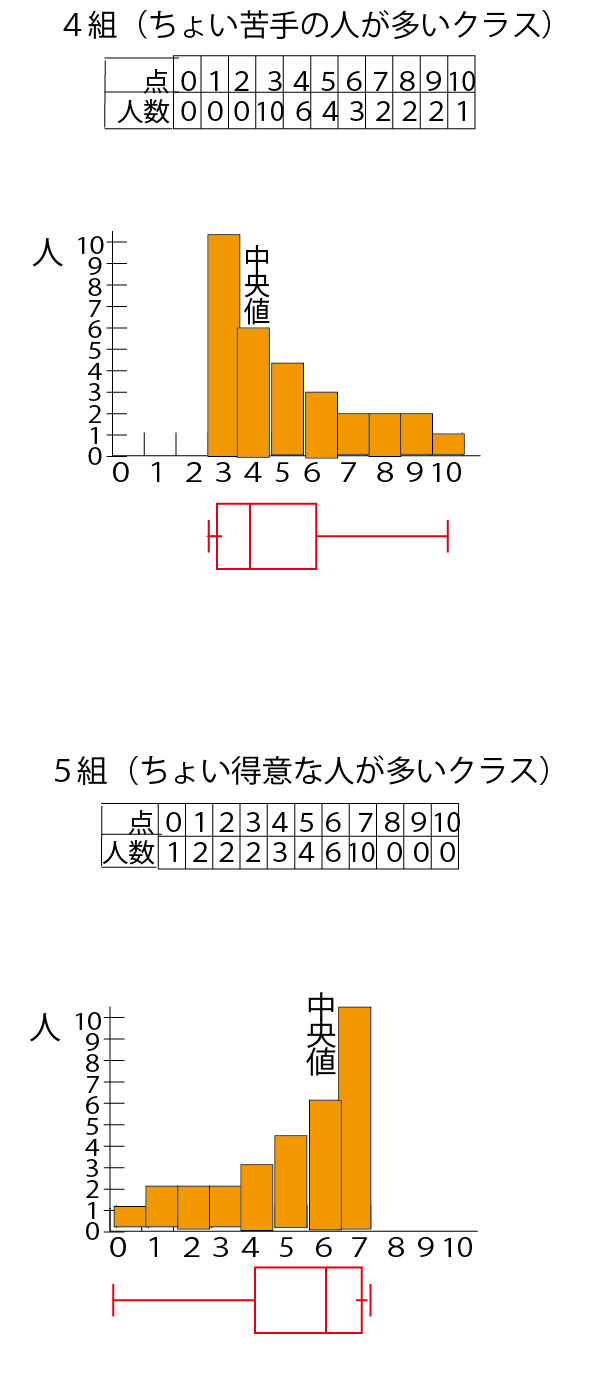
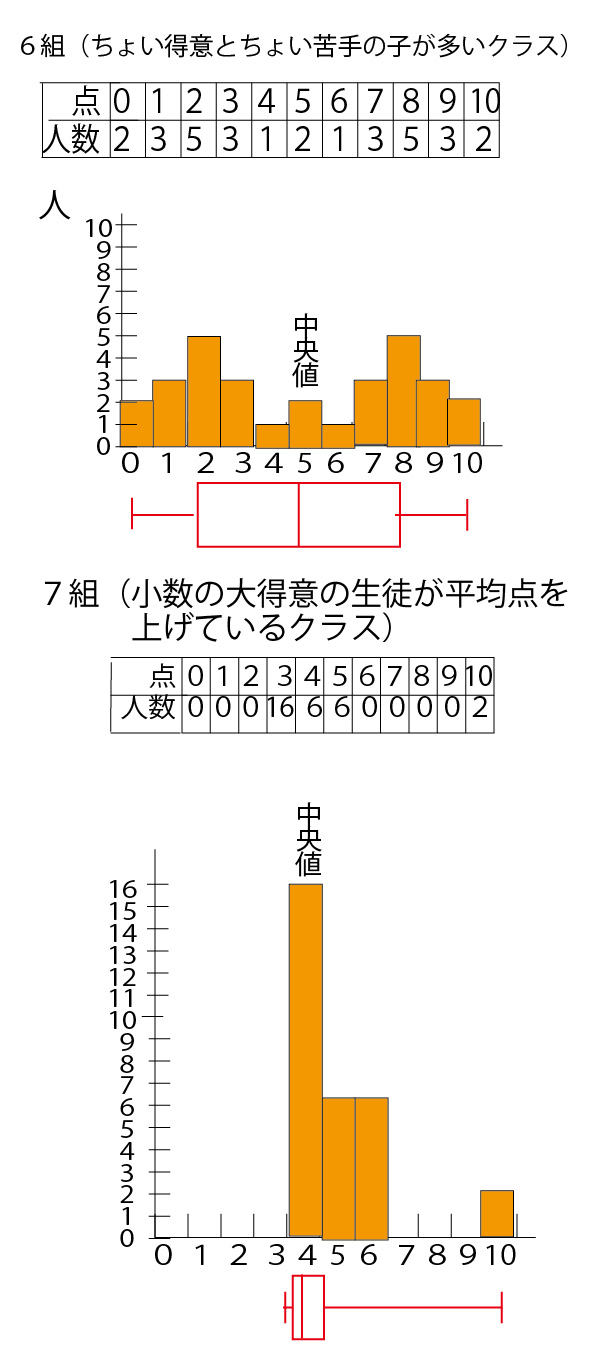
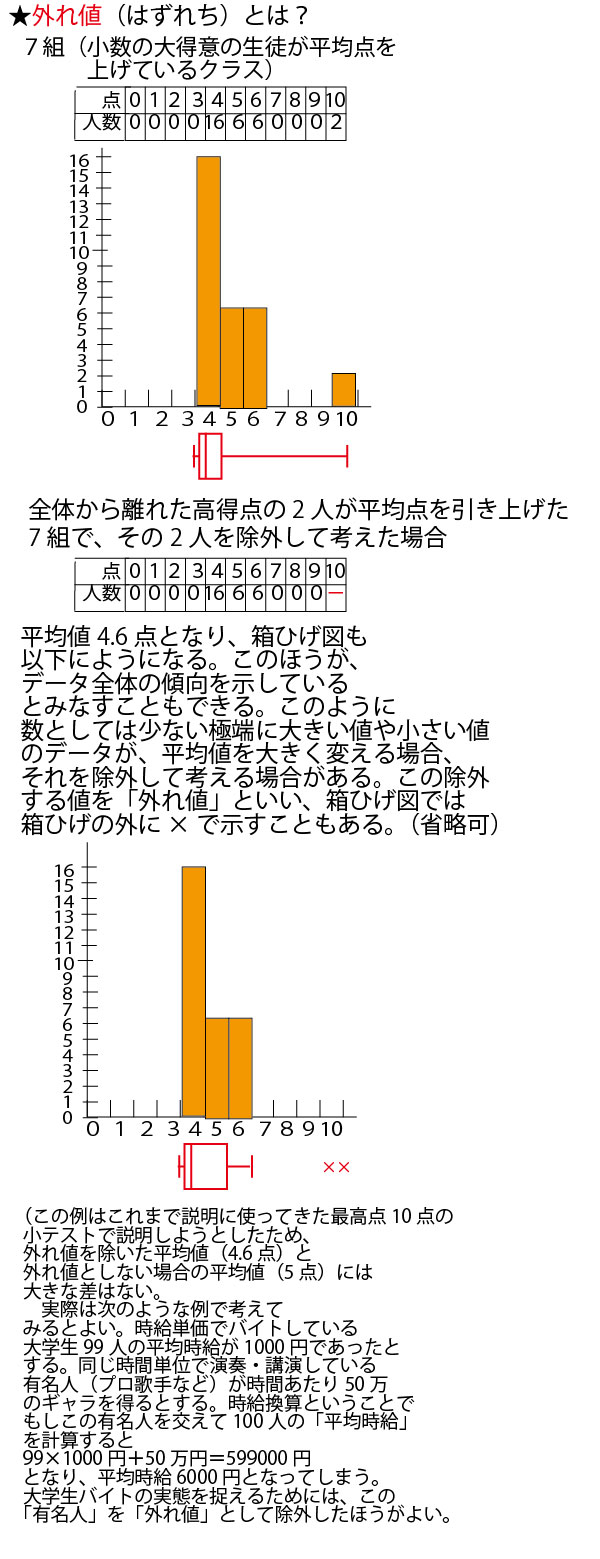

分散・標準偏差に関しては、最初に考えるのは30人クラスでは大きすぎて考えにくいので、まずは、平均点がいずれも5点となる5人組の5班(1班~5班)を例に考えていこう。