2023年大学入試共通テスト「数学IA」第4問（選択、20点）問題・解答・解説

アイ・ウエオカ
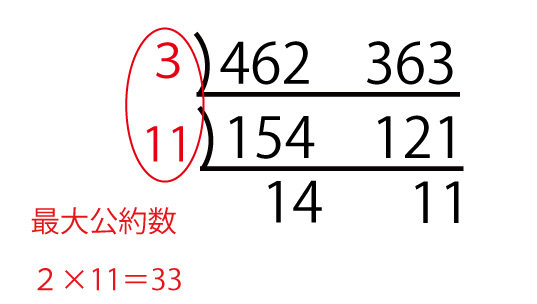
2数の最大公約数・最小公倍数を求めることができる「すだれ算」を使う。

すだれ算では左の2数をともに割り切ることのできる素数（2数の共通の約数）を２・３・５・７・11・13・・・・と小さい素数順に探していく。
462と100が2でともに割る切ることができる（共通の約数である）ことはすぐわかる。次の231と55は２でも３でも５でも７でもともには割り切ることができず（２・３・５・７は共通の約数ではなく）、11で初めてともに割り切ることができる（11が共通の約数である）。21と５は共通に割り切ることのできる素数はなくすだれ算は終了する。
両方を割り切ることのできる素数は２と11であり、最も大きい素数は11（アイ答）（2点）である。
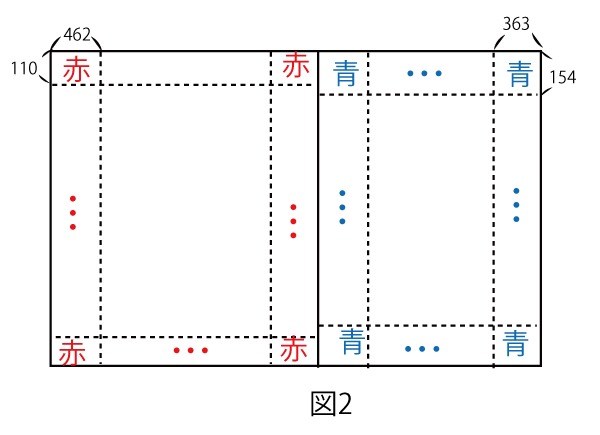
赤い長方形を並べて作ることができる正方形は、462と110の最小公倍数が、最小の辺の長さとなるので、その正方形の一片の長さは最小公倍数である2310（ウエオカ答）（3点）のものである。

キク・ケコサシ

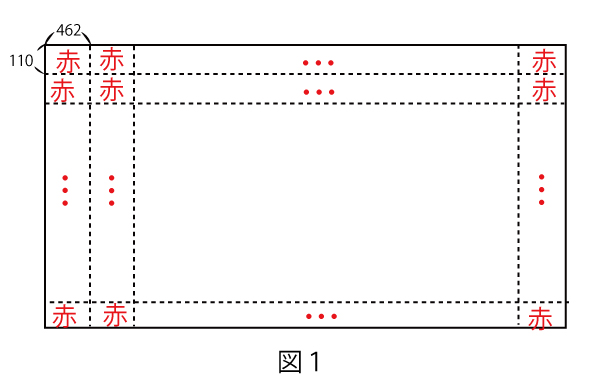
長方形１つの横の長さは462、縦の長さは110で、その最大公約数に注目すると
462＝22×21
110＝22×５
で正方形とならない並べ方で、横と縦の長さの差がある場合は22の倍数どうしの差なので、その差は22の倍数である。したがって、最小の差は22×１＝22（キク答）（3点）である。

横の個数をｍ個、縦の個数をｎ個とすると
横の長さ＝22×21ｍ
縦の長さ＝22×5n
縦のほうが長く、この差が22（キク）でなので
22×5nー22×21ｍ＝22
両辺を22で割って
5nー21ｍ＝１
5n（５の倍数）と21ｍ（21の倍数）で5nのほうが大きく、その差が１となる最小のmはｍ＝４（枚）で21ｍ＝21×４＝84、ｎ＝17で5n＝５×17＝85の時である。
横の長さは462×４個＝1848（ケコサシ答）（３点）

スセソ

このとき、赤い長方形を並べてできる長方形の縦の長さと、青い長方形を並べてできる長方形の縦の長さは等しい。よって、図２のような長方形のうち、縦の長さが最小のものは、110と154の最小公倍数となる。

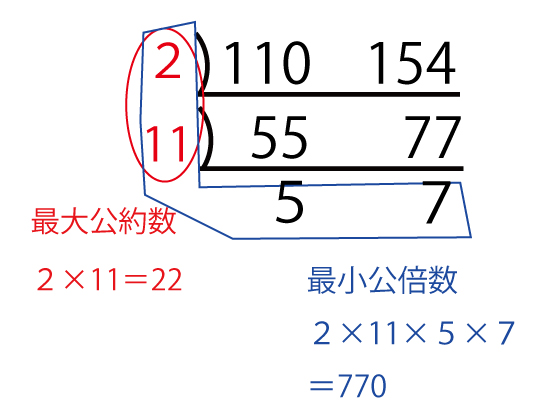
縦の長さはスセソ（770）（2点）のものであり、図２のような長方形は縦の長さがスセソ（770）の倍数である。

タチ・ツテトナ

462と363の最大公約数はタチ（33）（2点）である。

タチ（33）の倍数のうちでもスセソ（770）の倍数である最小の正の整数はツテトナ（2310）（2点）である。

ニヌネノ

全体が正方形になる時に横に並べる赤い長方形の数をｐ枚、青い長方形の数をq枚とすると、横の長さは462p+363q。これが2310の倍数なので
462ｐ＋363q＝2310ｒ

33で割って
14ｐ＋11q＝70r
11q＝70r－14p
11q=7（5r－2p)
11と７は互いに素なので
qが７の倍数、5rー2pが11の倍数である必要がある。
qが最小で7のとき、5r－2p=11。r=3、p=2のとき成り立つ。
よってこのときの正方形の1辺の長さは2310r=2310×３＝6930（ニヌネノ答）（3点）