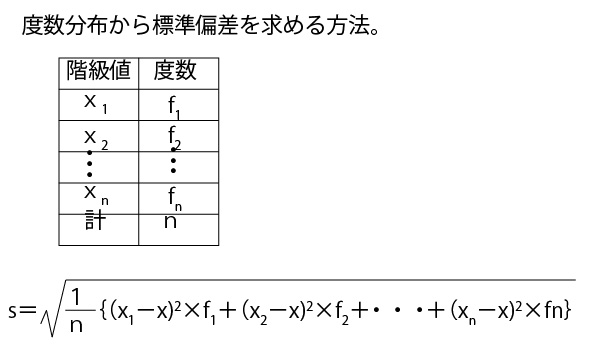
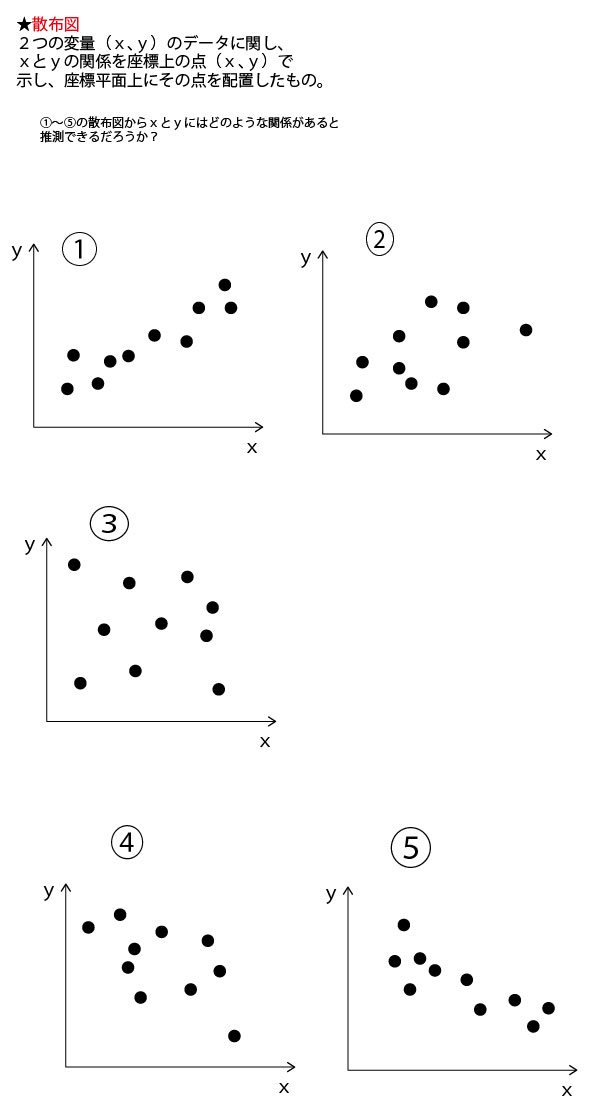
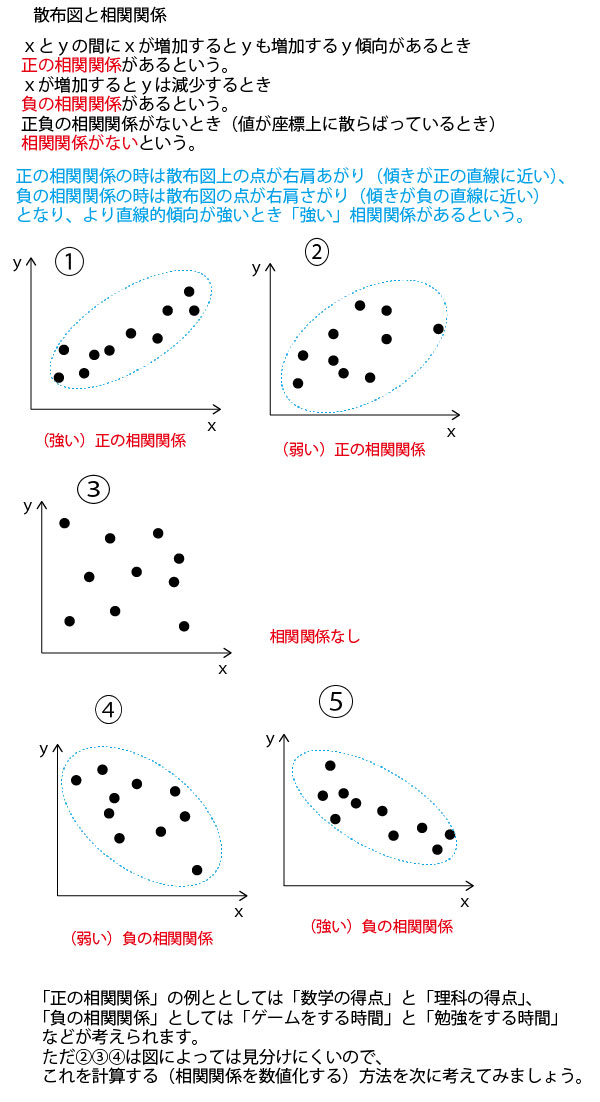
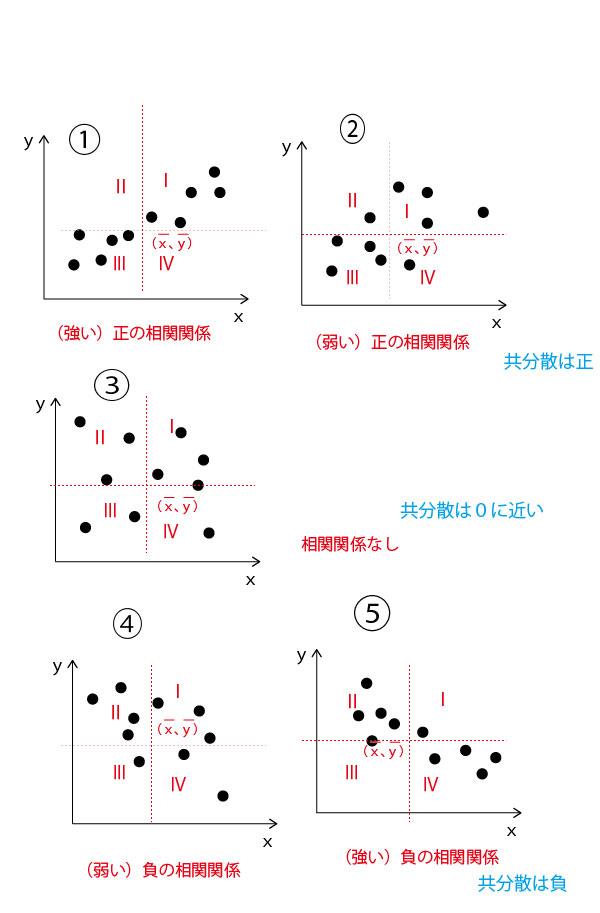
2024年　＃大学入試　＃共通テスト　＃数学１A　第2問［２］（配点15点）　問題・解答・解説

【解説】
（1）（i)サ・シ

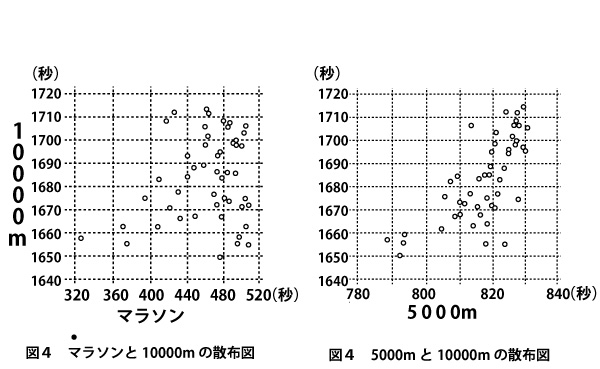
最頻値はもっとも度数が多い階級（ヒストグラムで高い値の階級）なので、サ。
度数50のデータで中央値は速い順に並べた時、25番目と26番目の値の平均値である。

度数分布表を作ると、25番目と26番目は共に420以上450未満の階級に含まれる。よってシ。

（ii)

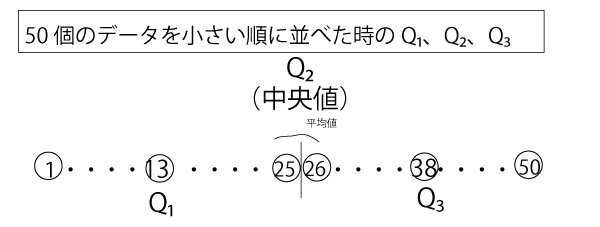
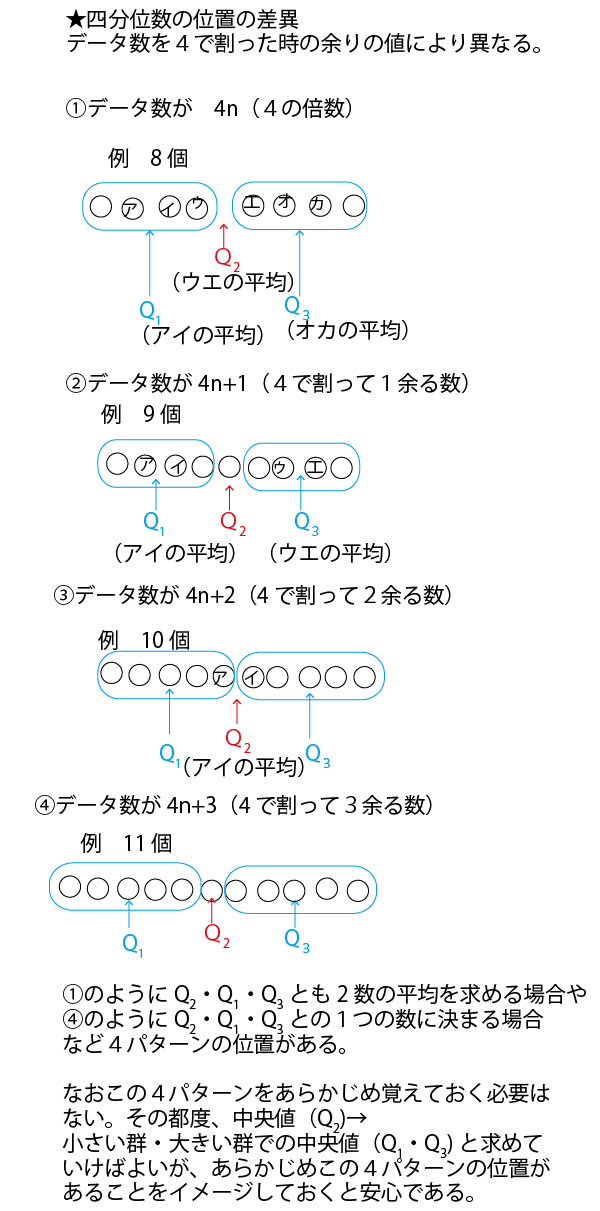
よって速い方から13番目の選手のベストタイムがQ₁である。四分位範囲はQ₃ーQ₁である。

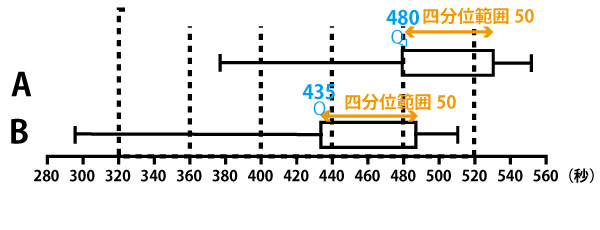
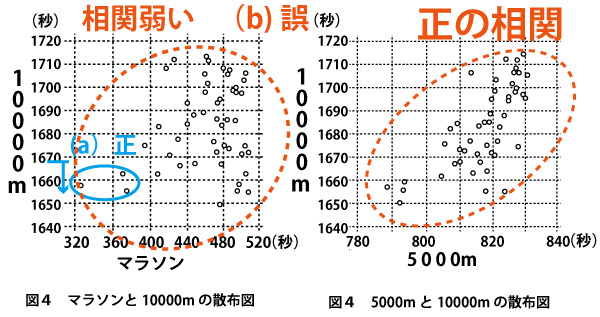
共通テストの図は値が正確に決定できない図となっているが、若干の読みのずれがあっても、正解の選択肢を選べるような図になっているので安心して、図の値を数値として読み取り計算してほしい。上図は読み取りの一例である。
Q₁の値の差は、480ー435＝45秒　ス。
四分位範囲の差の絶対値は、｜50ー50｜＝０。セ

（iii)
式を変形する
（あるデータのある選手のベストタイム）＝
（そのデータの平均値）＋ｚ×（そのデータの標準偏差）

ｚ×（そのデータの標準偏差）＋（そのデータの平均値）＝（あるデータのある選手のベストタイム）

ｚ×（そのデータの標準偏差）＝（あるデータのある選手のベストタイム）ー（そのデータの平均値）

ｚ＝｛（あるデータのある選手のベストタイム）ー（そのデータの平均値）｝÷（そのデータの標準偏差）

これにBの値を代入すると
ｚ＝（296ー454）÷45＝－3.511…（ソタチ答）

同様にAの1位の選手の値を代入して計算すると
ｚ＝（376ー504）÷40＝－3.2

ベストタイムは　Bの1位の選手(296）がAの１位の選手（376）より速い。
ｚの値は、Bの１位の選手（－3.51）がAの1位の選手（－3.2)より小さく優れている。
ツ

 

（2）

散布図に書き込んだように、（a)は正しく、（b)は5000ｍと10000ｍの相関のほうが強いので、間違いである。よってテ

 

以下は中学・高校の統計分野の基礎事項の総まとめです。

↓以下は基礎知識のまとめです。

★【中学（中１「資料の整理」）】分野のまとめ

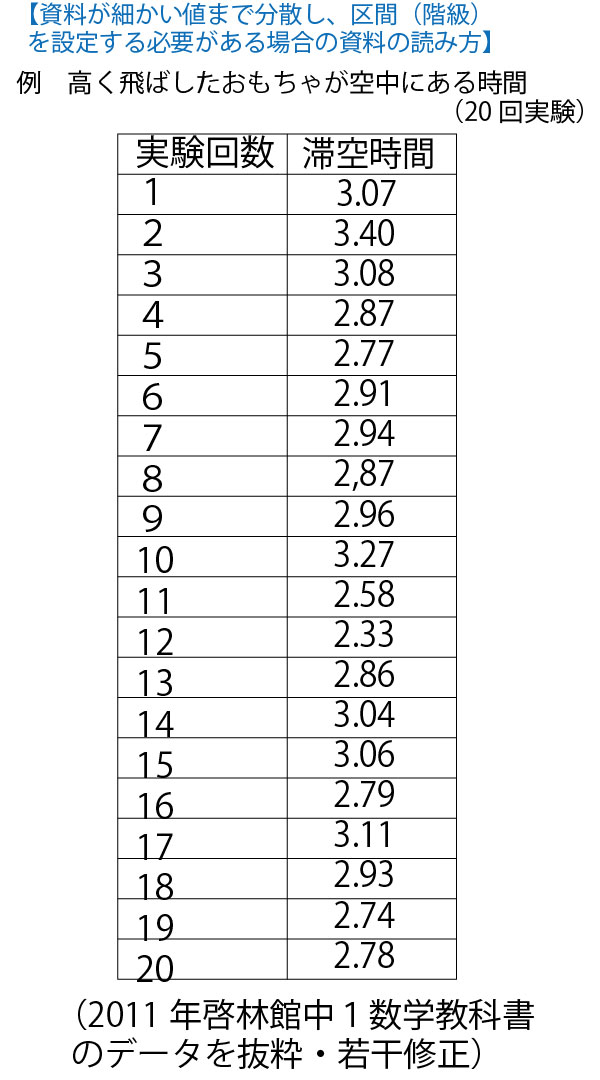
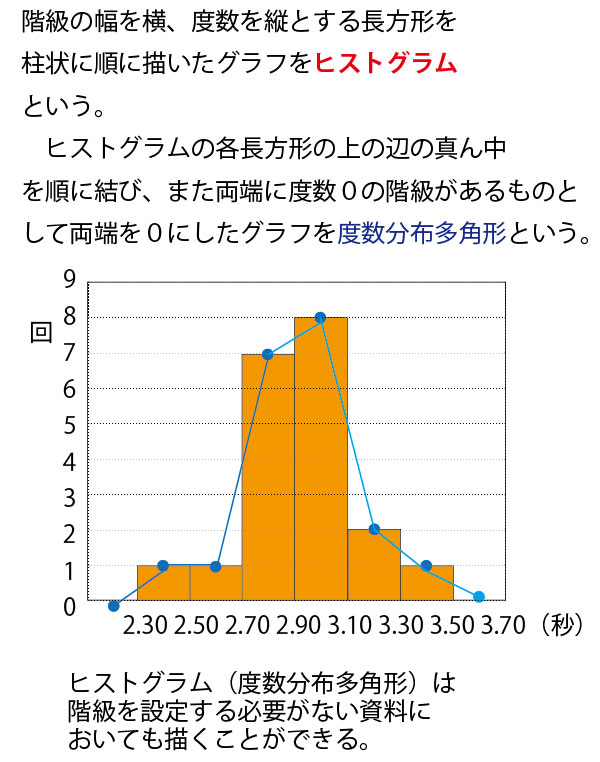
★高校数Ⅰ（データの分析）分野のまとめ。

中学１年で学ぶ「資料の整理」の発展編であり、この学問分野を統計学という。

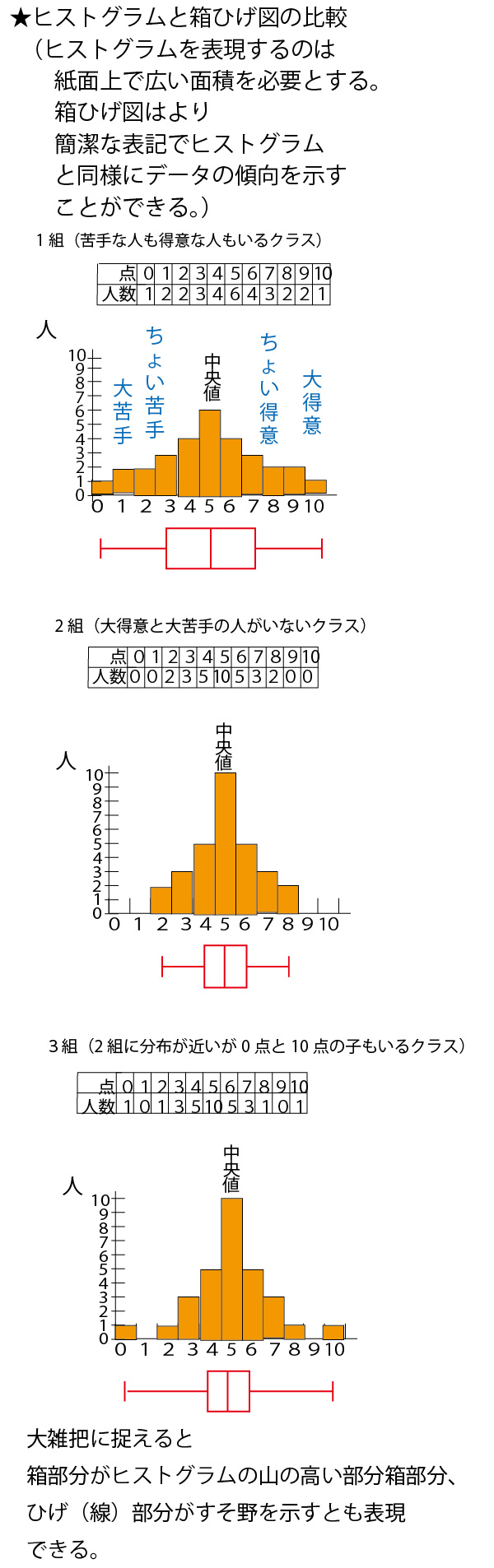
具体例として、数学の小テスト（10点満点）の平均点がいずれも5点が分布が異なる30人の７クラス（１組～7組）を例に考えていこう。

 

 

 

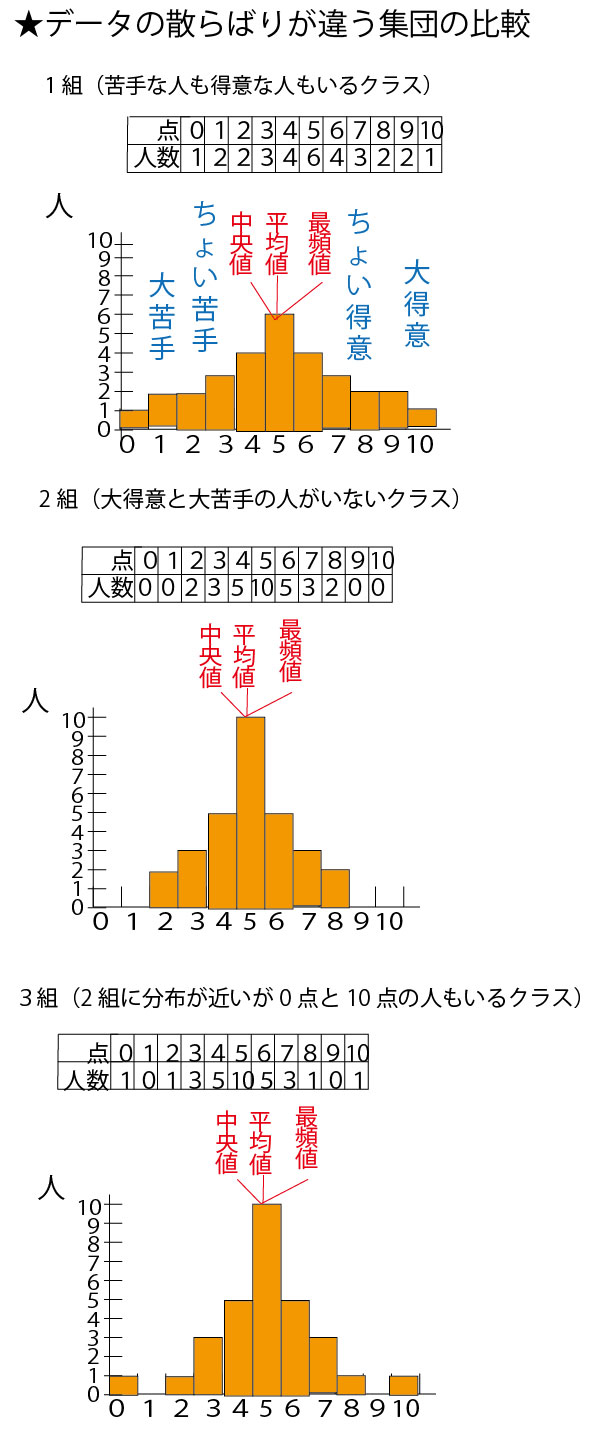
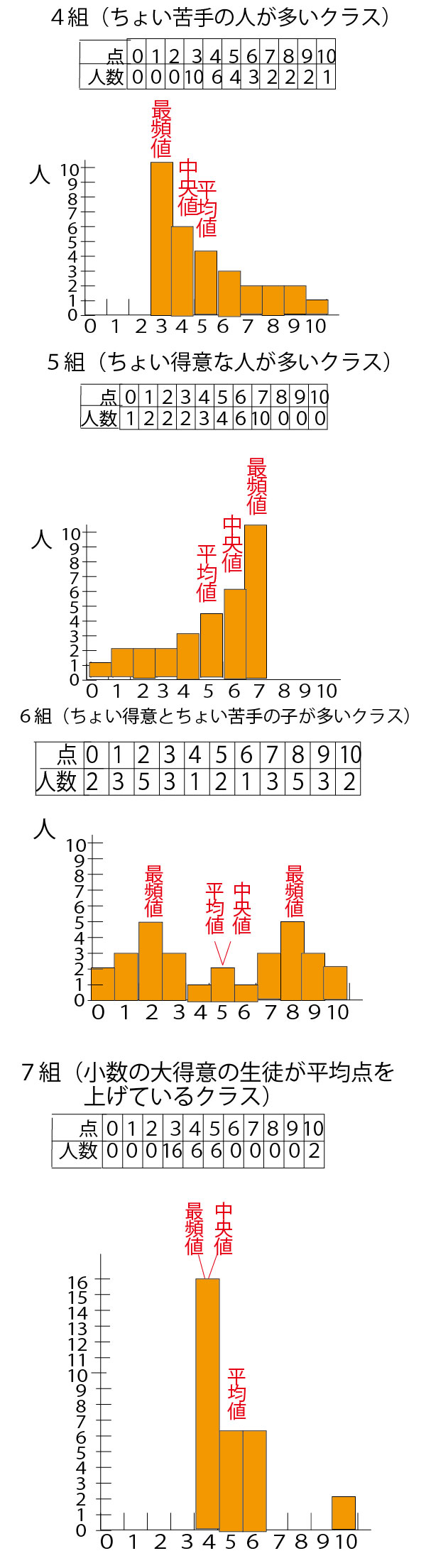
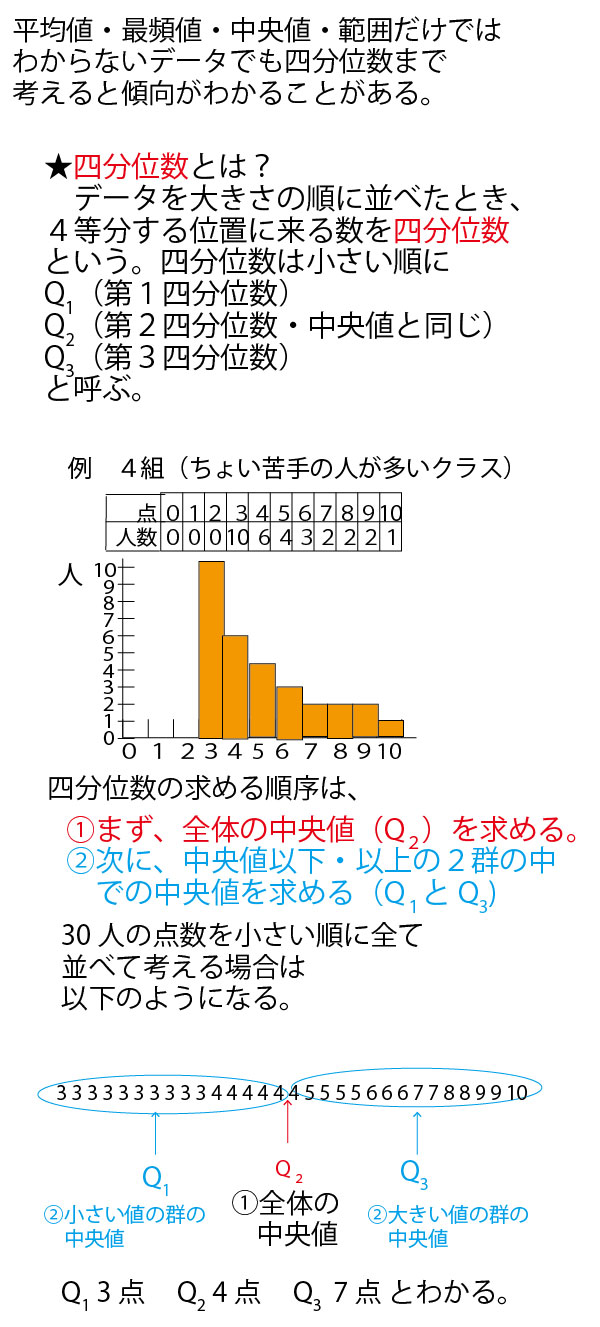
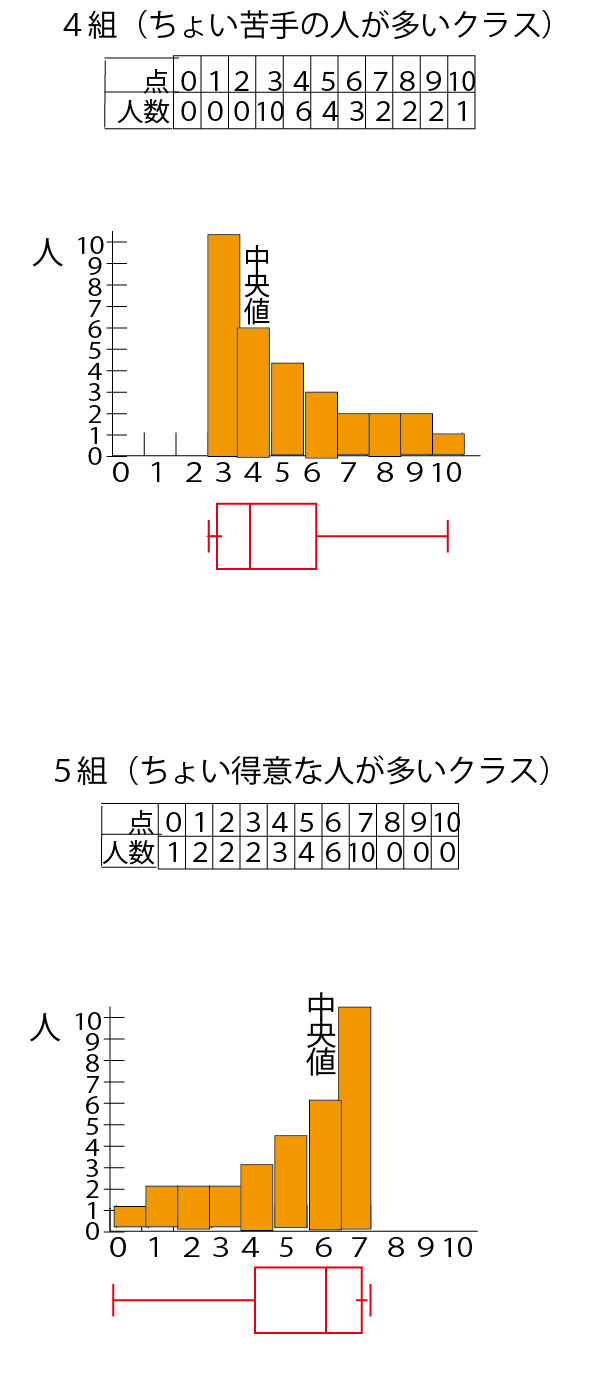
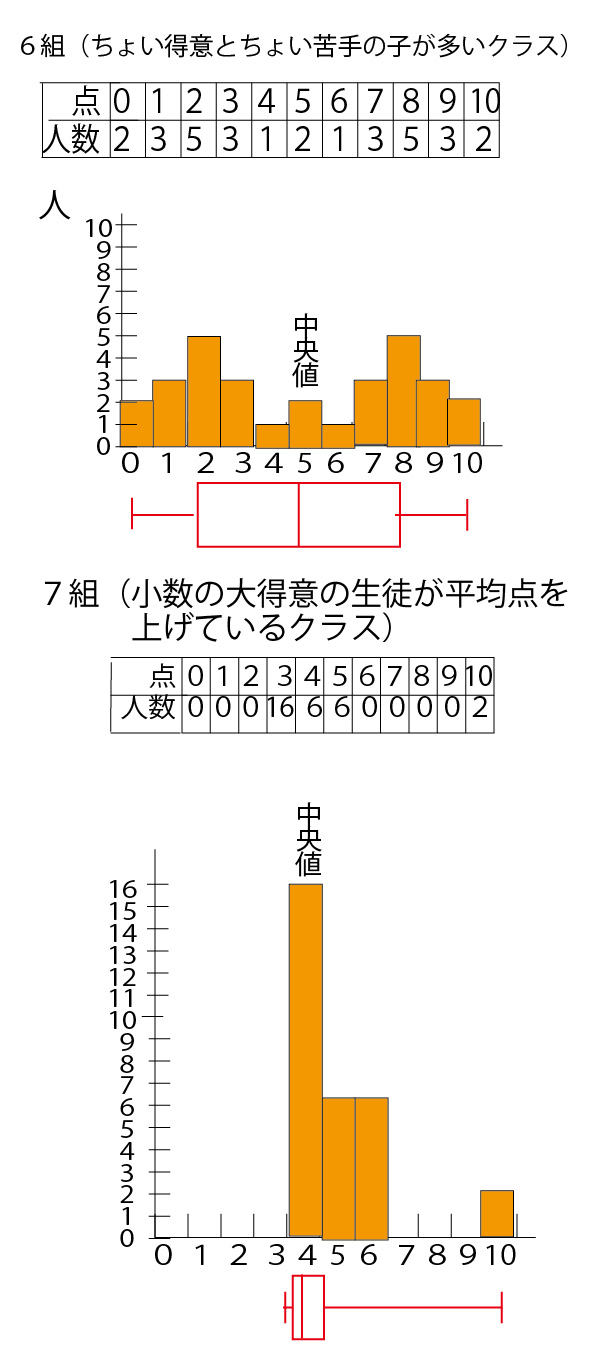
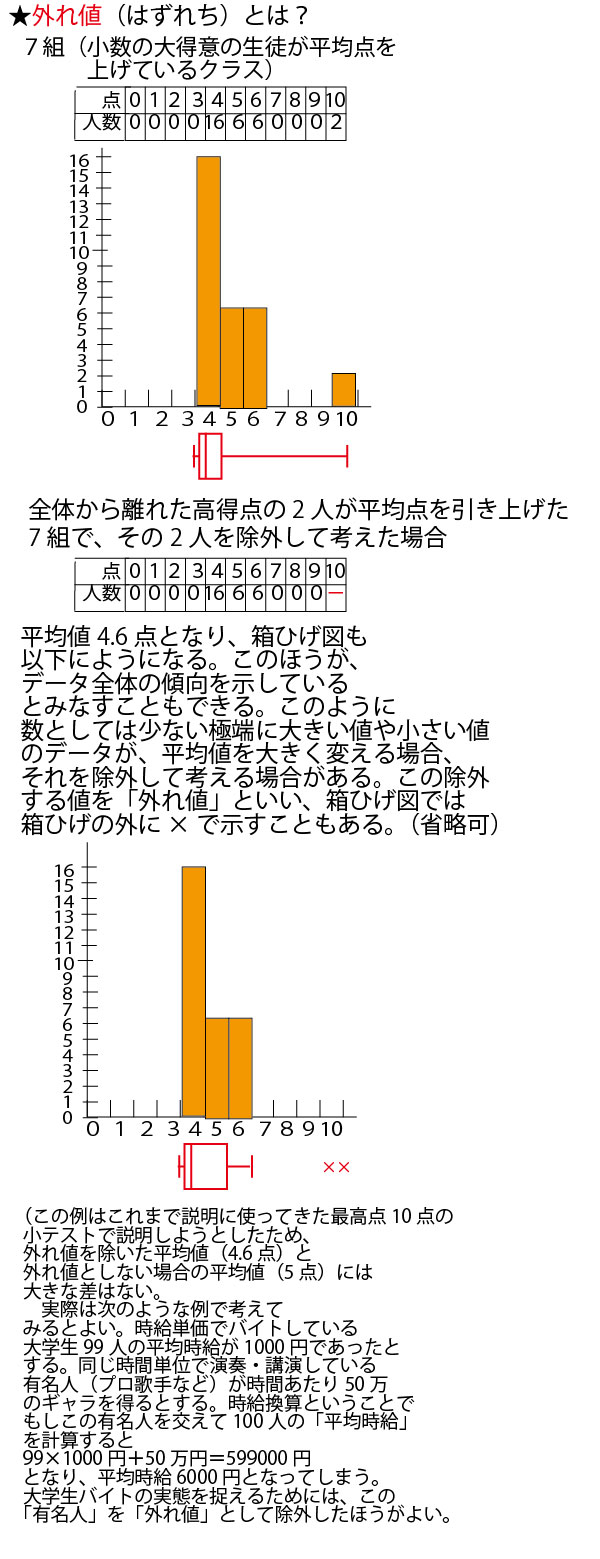
分散・標準偏差に関しては、最初に考えるのは30人クラスでは大きすぎて考えにくいので、まずは、平均点がいずれも5点となる5人組の５班（１班～５班）を例に考えていこう。