2023年大学入試共通テスト「数学IA」第4問（選択、20点）問題・解答・解説

2023年12月14日　予備校講師・船橋市議　朝倉幹晴

2023年大学入試共通テスト「数学１A」第4問（選択、配点20点）の解答・解説を作成しましたので、ご活用ください。問題文の最後の所でページ番号「２」をクリックすると解答・解説に飛びます。

2023年大学入試共通テスト「数学IA」第4問（選択、20点）

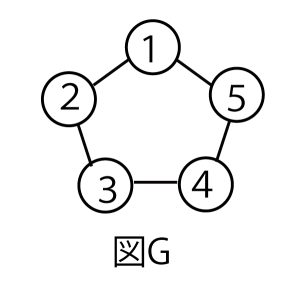
色のついた長方形を並べて正方形や長方形を作ることを考える。色のついた長方形は、向きを変えずにすき間なく並べることとし、色のついた長方形は十分（じゅうぶん）あるものとする。
（1）横の長さが462で縦の長さが110である赤い長方形を、図１のように並べて正方形や長方形を作ることを考える。462と110の両方を割り切る素数のうち最大のものはアイ（2点）である。

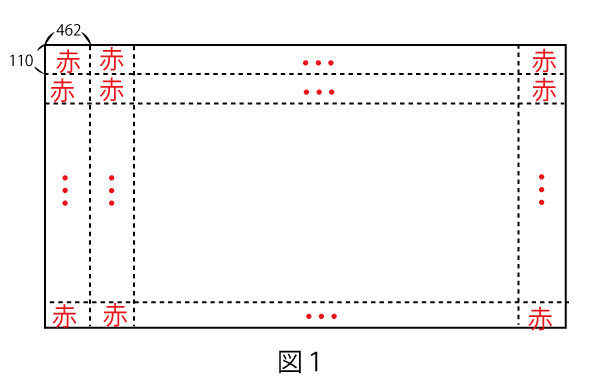
赤い長方形を並べて作ることができる正方形のうち、辺の長さが最小であるものは、一片の長さがウエオカ（3点）のものである。
また、赤い長方形を並べて正方形ではない長方形を作るとき、横の長さと縦の長さの差の絶対値が最小になるのは、462の約数と110の約数を考えると、差の絶対値がキク（3点）になるときであることがわかる。縦の長さが横の長さよりキク長い長方形のうち、横の長さが最小であるものは、横の長さがケコサシ（3点）のものである。
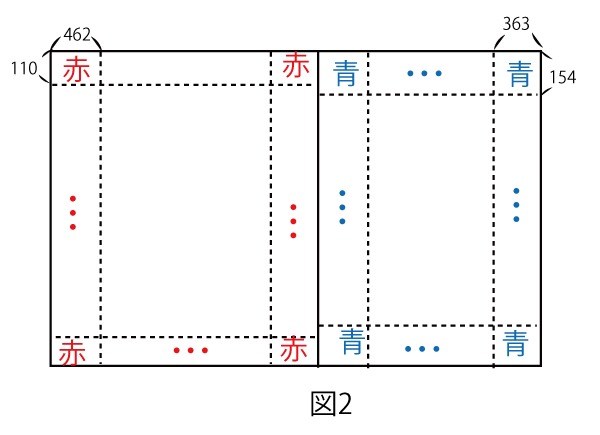
（2）花子さんと太郎さんは、（1)で用いた赤い長方形を1枚以上並べて長方形を作り、その右側に横の長さが363で縦の長さが154である青い長方形を1枚以上並べて、図２のような正方形や長方形を作ることを考えている。

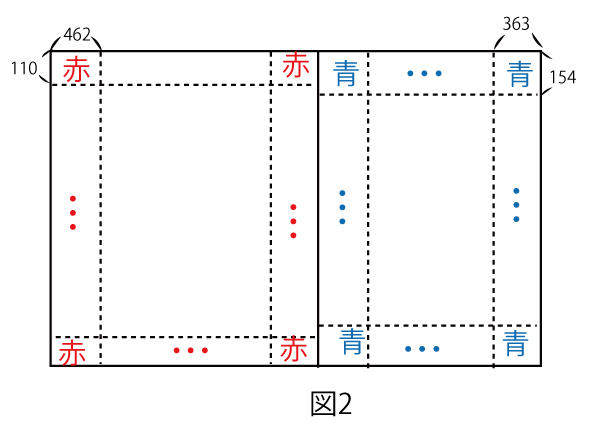
このとき、赤い長方形を並べてできる長方形の縦の長さと、青い長方形を並べてできる長方形の縦の長さは等しい。よって、図２のような長方形のうち、縦の長さが最小のものは、縦の長さがスセソ（2点）のものであり、図２のような長方形は縦の長さがスセソの倍数である。
二人は、次のように話している。

花子：赤い長方形と青い長方形を図２のように並べて正方形を作ってみようよ。
太郎：赤い長方形の横の長さが462で青い長方形の横の長さが363だから、図２のような正方形の横の長さは462と363を組み合わせて作ることができる長さでないといけないね。
花子：正方形だから、横の長さはスセソの倍数でもないといけないね。

462と363の最大公約数はタチ（2点）であり、タチの倍数のうちでもスセソの倍数である最小の正の整数はツテトナ（2点）である。
これらのことと、使う長方形の枚数が赤い長方形も1枚以上であることから、図２のような正方形のうち、辺の長さが最小であるものは、一辺の長さが二ヌネノ（3点）のものであることがわかる。
[next_p]