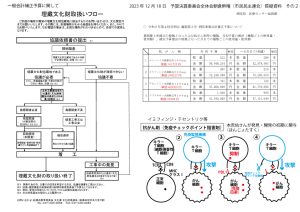
2023年大学入試共通テスト「数ⅡＢ」第1問[2]（配点12点）問題・解答・解説

2023年12月18日 2023年12月18日

asakura

2023年12月18日　予備校講師・船橋市議　朝倉幹晴

2023年大学入試共通テスト「数学2B」第1問［２］（配点12点）の解答・解説を作成しましたので、ご活用ください。問題文の最後の所でページ番号「２」をクリックすると解答・解説に飛びます。
ⅡBの解答解説は順次作成中（ⅡB第1問［１］は完成）ですが、IAは完成していますのでご活用ください。
2023年数学ⅡB第1問［１］（配点18点）問題・解答・解説
 2023年大学入試共通テスト数１A全問題・解答・解説

2023年大学入試共通テスト「数学ⅡA」第2問（12点）

[２]（1）a＞0、a≠１、ｂ＞０のときlog_ab＝ｘとおくと、ツ（3点）が成り立つ。

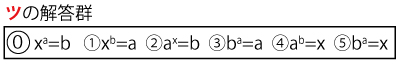
（2）様々な対数の値が有理数か無理数かについて考えよう。

（ⅰⅰ）log₂3が有理数と無理数のどちらであるか考えよう。
log₂3が有理数であると仮定すると、log₂3＞0であるので、二つの自然数p,qを用いて

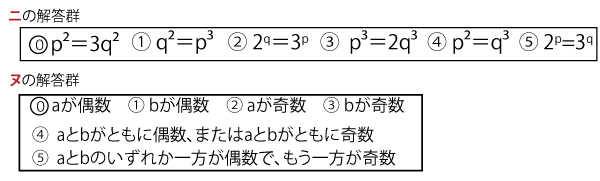
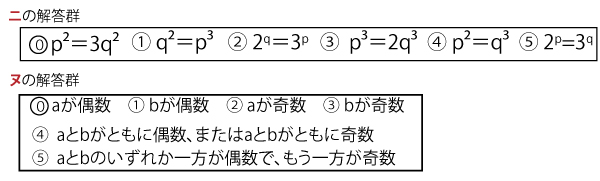
いま、２は偶数であり３は奇数であるので、ニを満たす自然数p、qは存在しない。
したがって、log₂3は無理数であることがわかる。