2023年大学入試共通テスト「数ⅡＢ」第1問[1]（配点18点）問題・解答・解説

2023年12月16日 2023年12月23日

asakura

2023年12月16日　予備校講師・船橋市議　朝倉幹晴

2023年大学入試共通テスト「数学2B」第1問［1］（配点18点）の解答・解説を作成しましたので、ご活用ください。問題文の最後の所でページ番号「２」をクリックすると解答・解説に飛びます。
ⅡBの解答解説は順次作成中ですが、IAは完成していますのでご活用ください。
2023年大学入試共通テスト数１A全問題・解答・解説

（2)sinxとsin2xの値の大小関係を詳しく調べよう。

sin2x－sinx＝sinx（ウcosx－エ）　（ウエあわせて2点）
であるから、sin2x－sinx＞0が成り立つことは
「sinx>0かつウcosx－エ＞０」・・・・

または
「sinx<0かつウcosx－エ＜０」・・・・
が成り立つことと同値である。０≦ｘ≦2πのとき、が成り立つようなxの値の範囲は

であり、が成り立つようなｘの値の範囲は

である。よって、０≦ｘ≦2πのとき、sin2x＞sinxが成り立つようなｘの値の範囲は

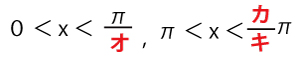
である。
（3）sin3xとsin4xの値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
sin(α＋β）－sin（αーβ）＝2cosαsinβ・・・・
が得られる。α＋β＝4x、αーβ＝3xを満たすα、βに対してを用いることにより、
sin4x－sin3x＞０が成り立つことは
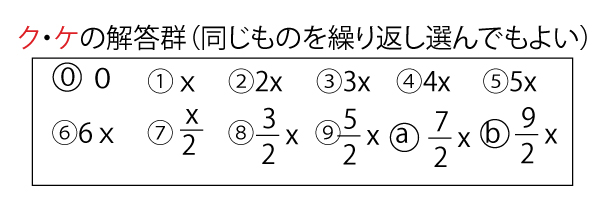
「cosク＞０　かつ　sinケ＞０」・・・・（クケ合わせて2点）
または
「cosク＜０　かつ　sinケ＜０」・・・・
が成り立つことと同値であることがわかる。
0≦ｘ≦πのとき、により、sin4x＞sin3xが成り立つようなｘの値の範囲は

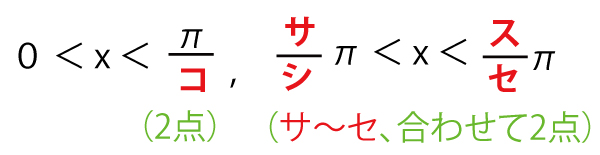
である。