2022年大学入試共通テスト数学ⅠA第2問[2](統計・配点15点)問題・解答・解説

【解説】
(1)29カ国を学習者数が少ない順に並べると以下のようになる。
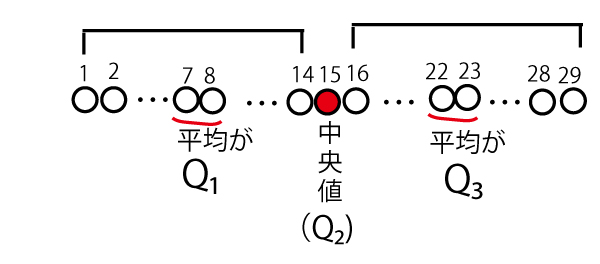
中央値Q2は15番目の国の値となり、Q1は1~14番目の国の中央値なので7・8番目の国の値の平均値となる。
Q3は16~29番目の国の中央値なので22・23番目の国の値の平均値となる。
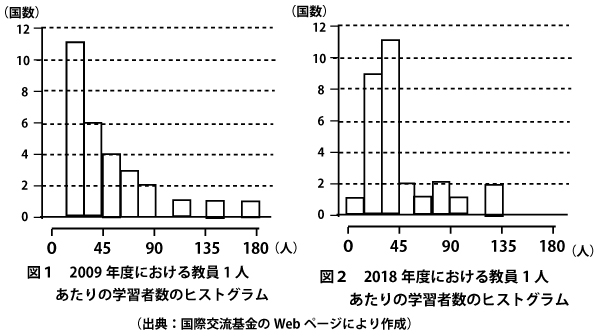
小さい値からのヒストグラムを度数分布表に直し、小さい値からの累積度数を考えると以下のようになる。

・2009年度と2018年度の中央値(Q2、15番目の国)が含まれる階級の階級値を比較すると、共に30~45の階級で、階級値は共に37.5となるので、両者は等しい。(ケ答、![]() )
)
・2009年度と2018年度の第1四分位数(Q1)が含まれる階級の階級値を比較すると、共に15~30の階級で階級値は共に22.5となるので、両者は等しい。(コ答、![]() )
)
・2009年度と2018年度の第3四分位数(Q3)が含まれる階級の階級値を比較すると、2009年度は60~75階級で階級値は67.5、2018年は45~60階級で階級値は52,5で、2018年度のほうが小さい。(サ答、![]() )
)
(ケコサ、あわせて3点)
範囲は、2009年度は、最小値は「15~30階級」に存在し、最大値は「165~180階級」に存在するので、最小範囲で165ー30=135、最大範囲で180ー15=165、つまり135~165が範囲となりうる。
2018年度は、最小値は「0~15階級」に存在し、最大値は「120~135階級」に存在するので、最小範囲で120ー15=105、最大範囲で135ー0=135、つまり105~135が範囲となりうる。
しながって2018年度のほうが小さい。(シ答、![]() )
)
四分位範囲はQ3-Q1である。
2009年度ではQ3は「60~75階級」に存在し、Q1は「15~30階級」に存在するので、最小範囲で60ー30=30、最大範囲で75ー15=60。つまり30~60が四分位範囲となりうる。
2018年度ではQ3は「45~60階級」に存在し、Q1は「15~30階級」に存在するので、最小範囲で45ー30=15、最大範囲で60ー15=45、つまり15~45が四分位範囲となりうる。
両者が共に30~45の範囲であった場合、その大小はわからない。
これら二つのヒストグラムからだけでは両者の大小を判断できない。(ス答、![]() )
)
(シス、あわせて2点)
(2)
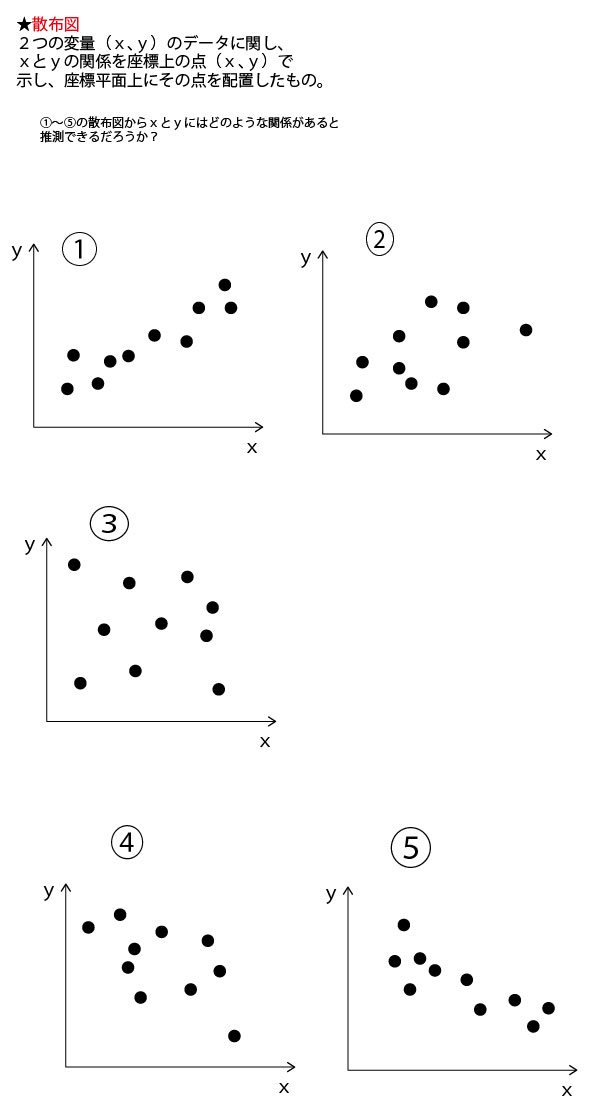
選択肢の3図とも散布の概形は似ているので、その比較で選ぶのは難しい。そこで最大値・最小値を考えてみる。
図3の箱ひげ図より、「教育機関1機関あたりの学習者」は最小50人、最大は480人である。
選択肢の散布図では横軸が「教育機関1機関あたりの学習者」で、いずれも最小が50人である点は一致している。しかし最大については![]()
![]()
![]() が480人ぐらいであるのに対し、
が480人ぐらいであるのに対し、![]() は420人なので
は420人なので![]() は答ではない。
は答ではない。
次に図3でQ1、Q3の値を確認し、それが、選択肢の散布図で横軸の値が小さい値から7番目・8番目の平均の値、大きい値から7番目・8番目の平均の値と一致するかどうかを確認する。
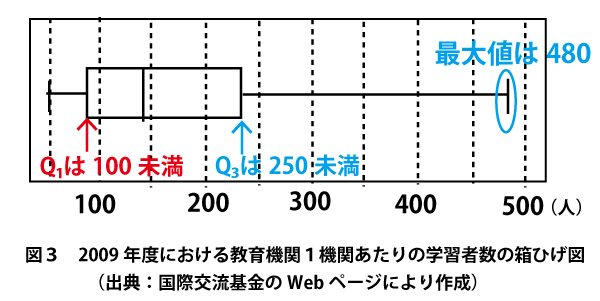
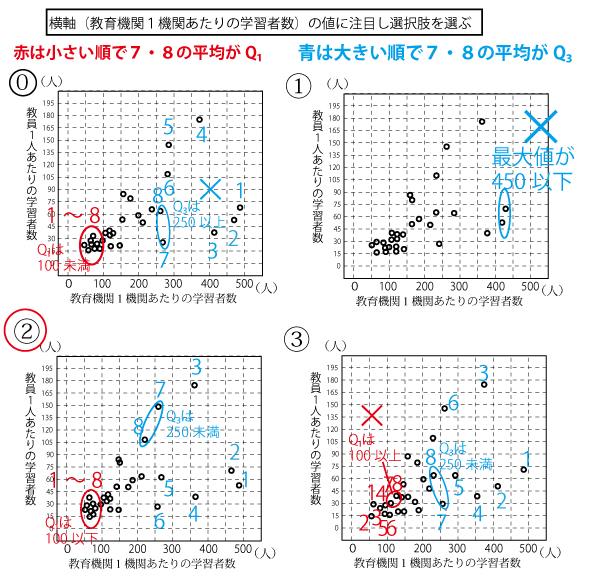
すると![]() はQ3が250以上となっているので誤り。
はQ3が250以上となっているので誤り。 はQ1が100以上となっているので誤り。
はQ1が100以上となっているので誤り。
最大値もQ1もQ3も全て適合しているのは、![]() である。(セ答、4点)
である。(セ答、4点)
(「教員1人あたりの学習者数」はヒストグラムで、最小が15~30、最大が165~180である。選択肢の散布図では縦軸が「教員1人あたりの学習者数」で、選択肢の全てが、最小が15~30、最大が165~180となっているので、その視点で選ぶことはできない。90~105、120~135、150~165の階級に値がないことも選択肢すべてが満たしているので、その点でも選ぶことがはできない。)(この視点は本設問では有効でなかったが、他の問題では有効になりうる視点なので、その視点も持っていてほしい。)
(3)
(4)
前問表1でのSの平均値(81.8)を縦軸、とTの平均値(72.9)を横軸として選択肢の散布図に書き入れてみる。

すると選択肢![]()
![]() は実際の図の値の平均値より、左・下にずれていることがわかり、正解でないとわかり、
は実際の図の値の平均値より、左・下にずれていることがわかり、正解でないとわかり、![]() か
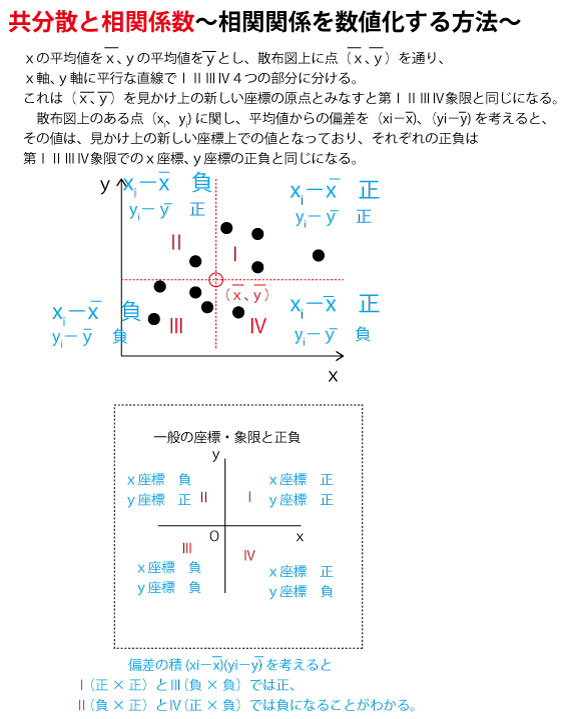
か![]() が答である。相関係数0.63は最高値1に近い「強い」正の相関関係なので、よりばらつきが少なく、右上がりの斜めの範囲内に値が集中している
が答である。相関係数0.63は最高値1に近い「強い」正の相関関係なので、よりばらつきが少なく、右上がりの斜めの範囲内に値が集中している![]() が答である。(ツ答、3点)
が答である。(ツ答、3点)
↓以下は基礎知識のまとめです。
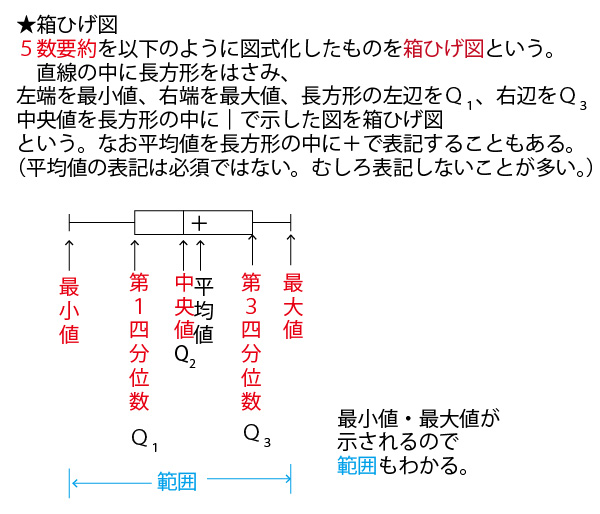
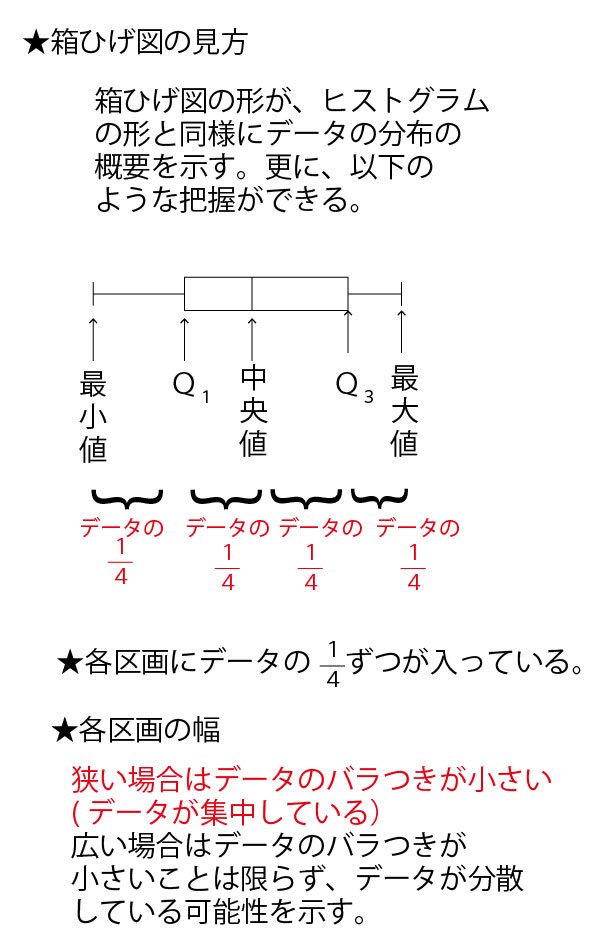
★【中学(中1「資料の整理」)】分野のまとめ

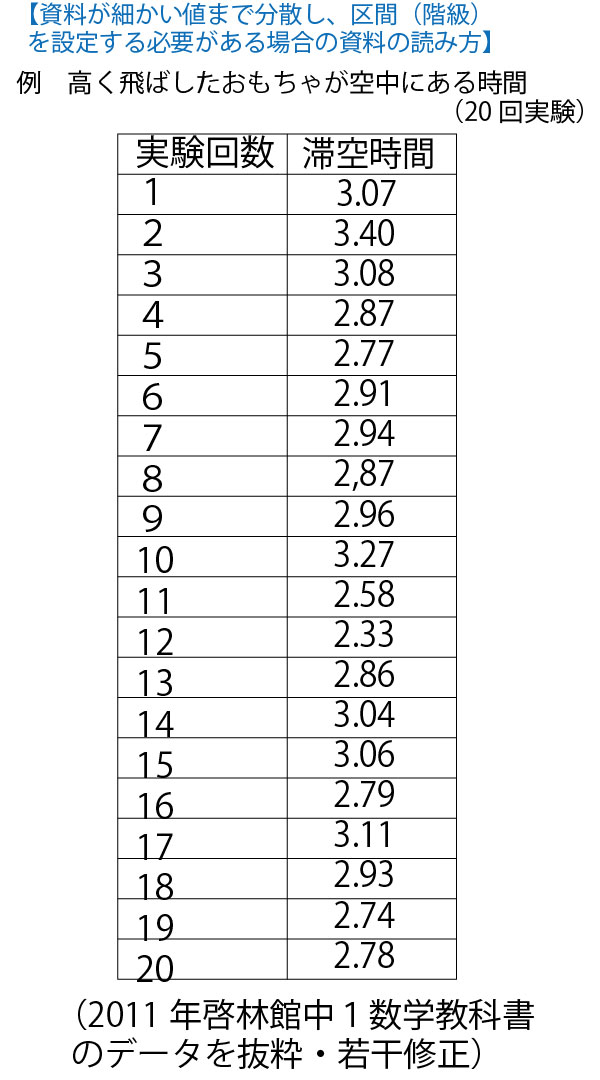

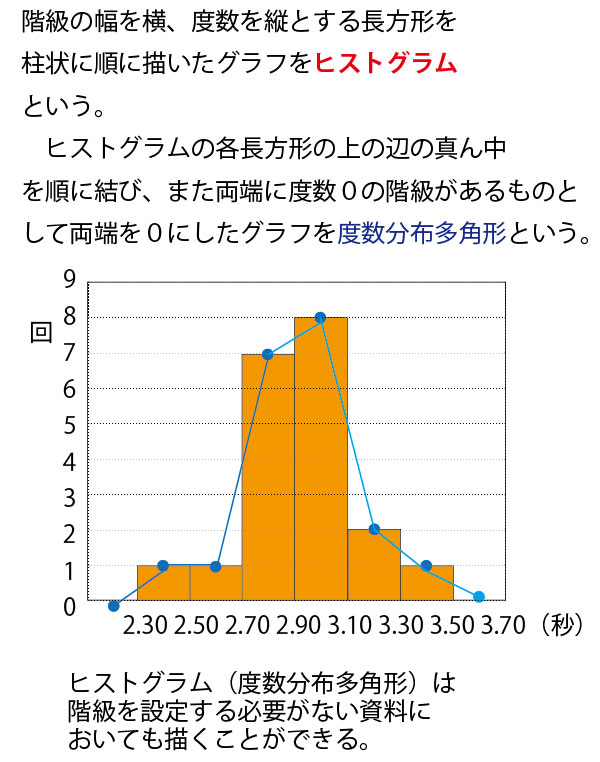
★高校数Ⅰ(データの分析)分野のまとめ。
中学1年で学ぶ「資料の整理」の発展編であり、この学問分野を統計学という。
具体例として、数学の小テスト(10点満点)の平均点がいずれも5点が分布が異なる30人の7クラス(1組~7組)を例に考えていこう。
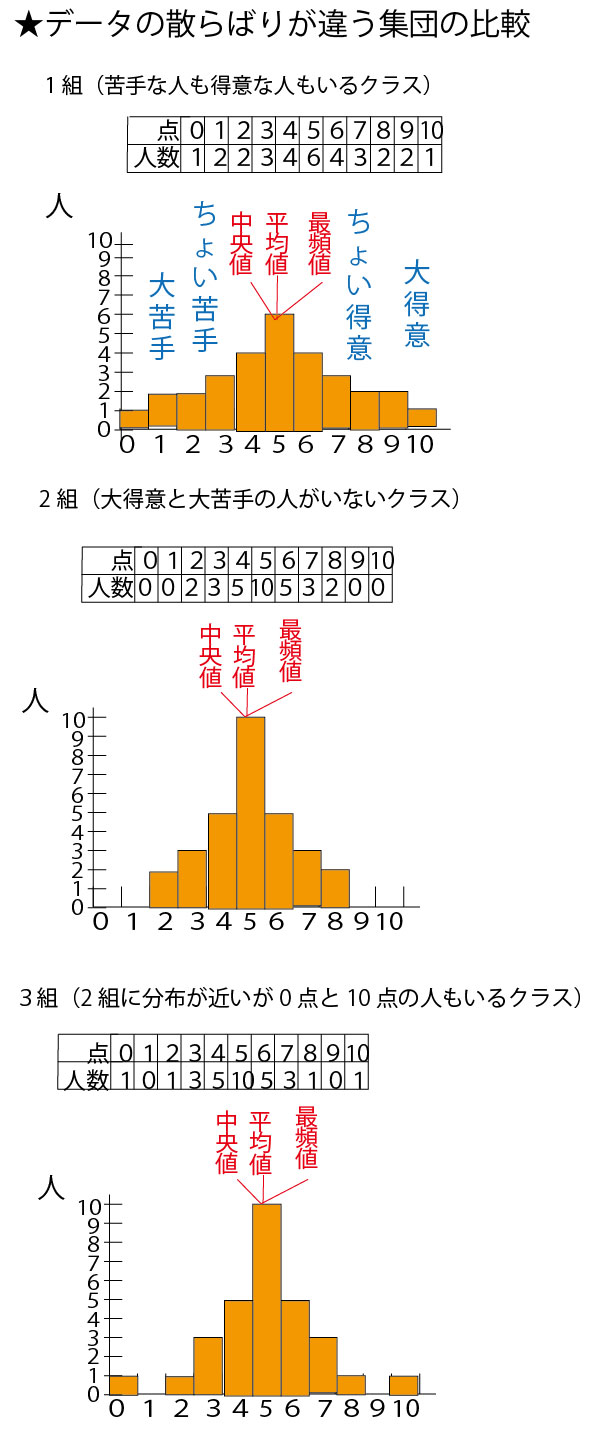
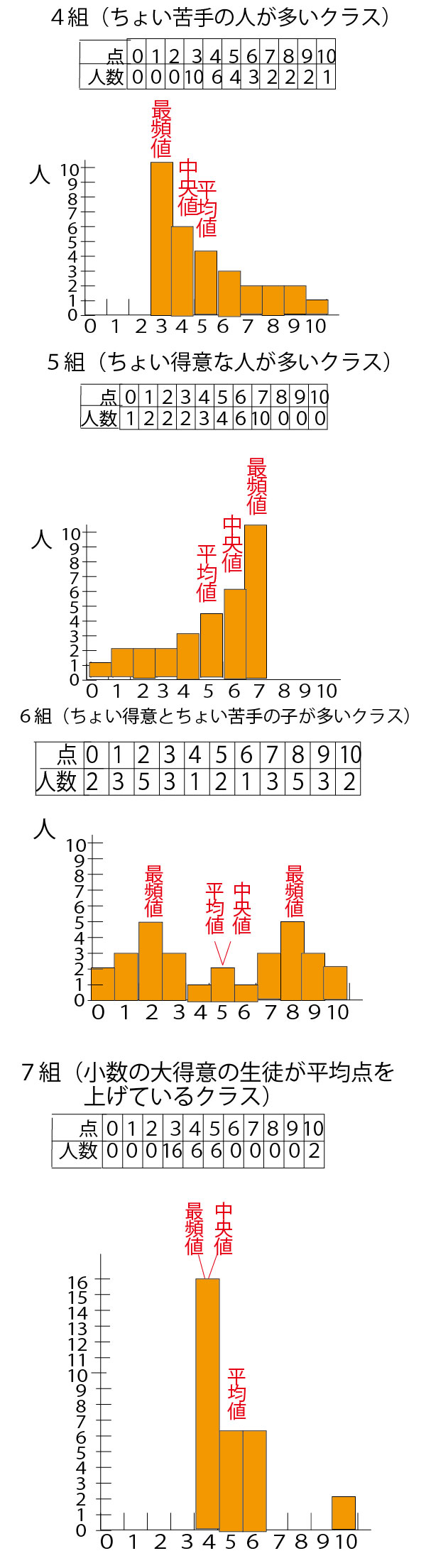


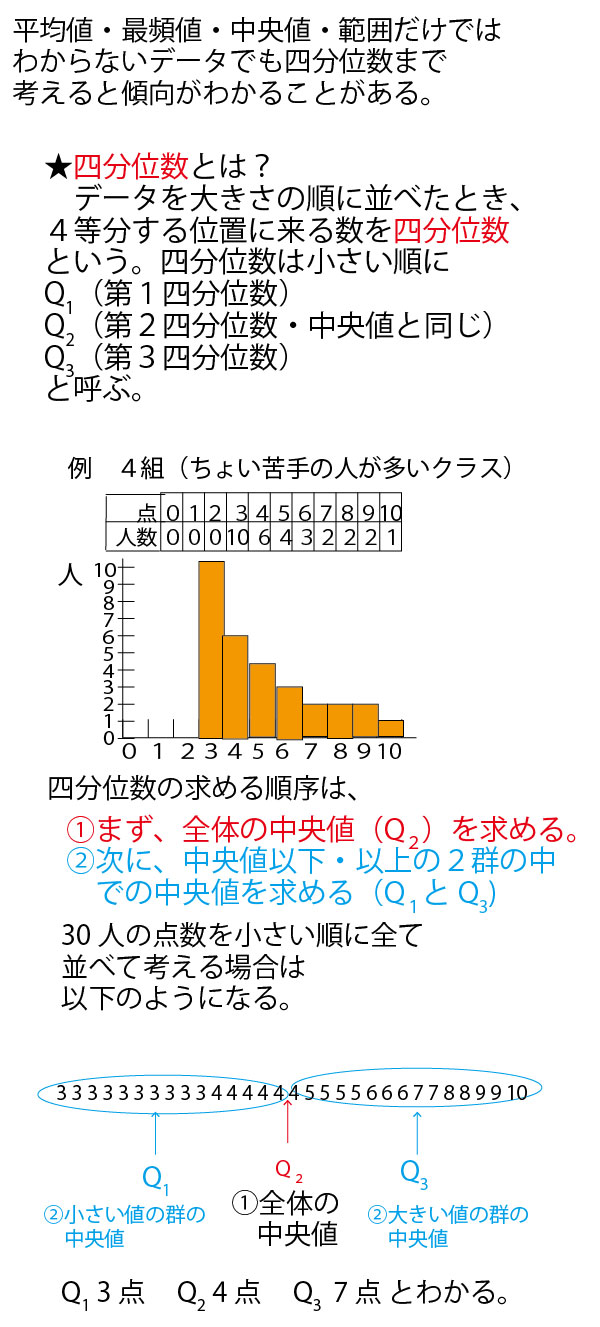
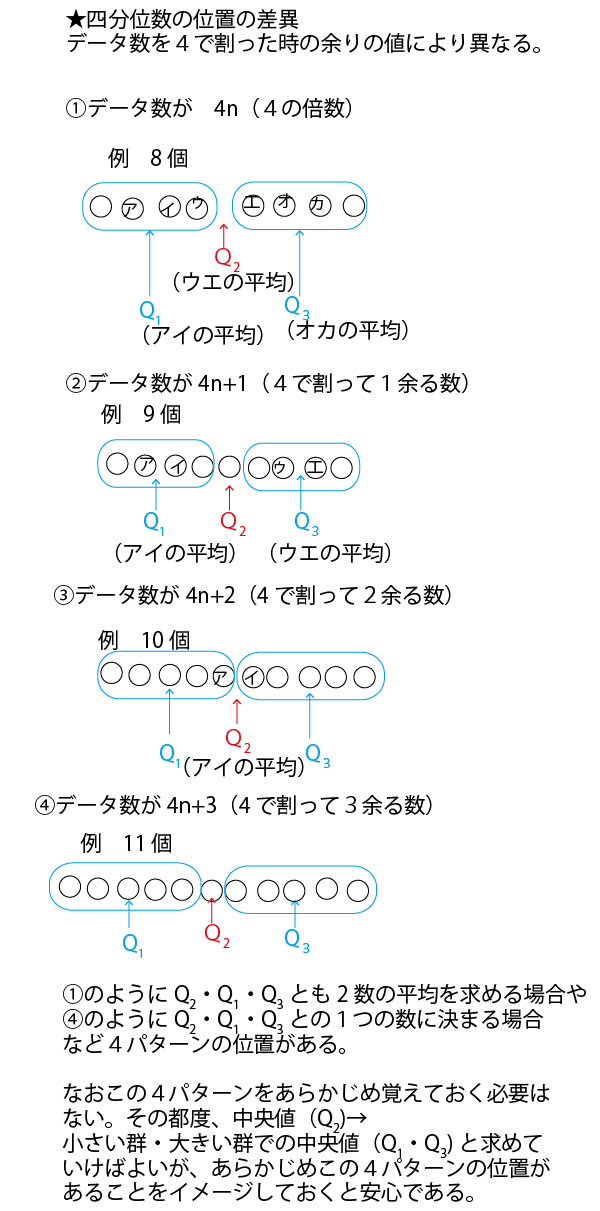




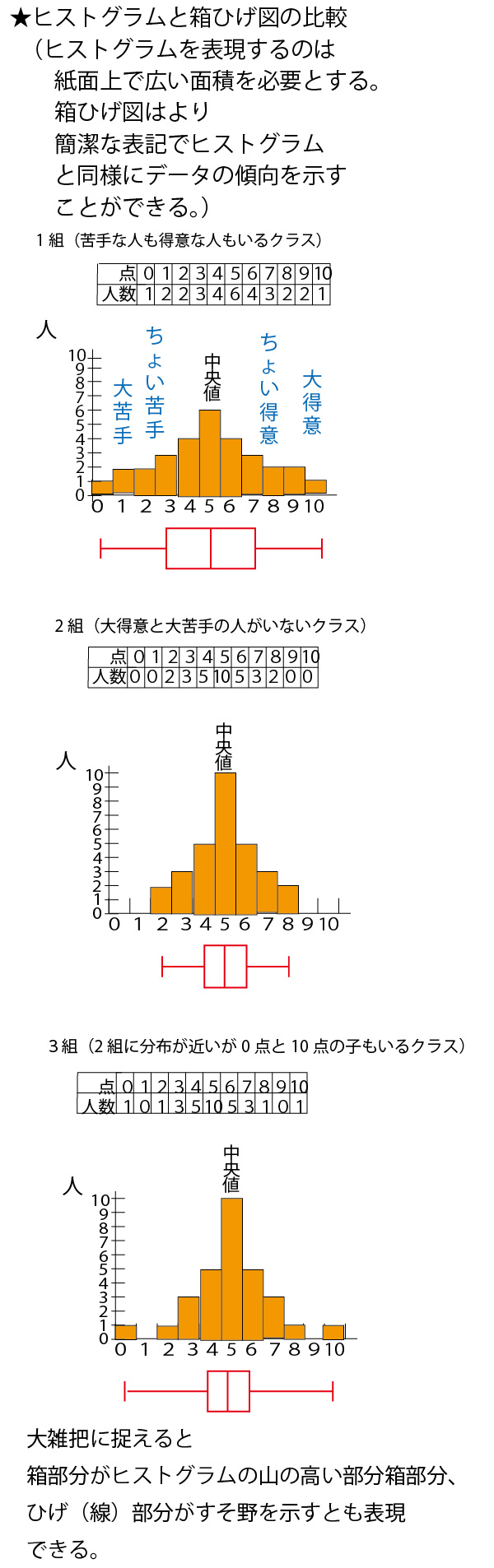
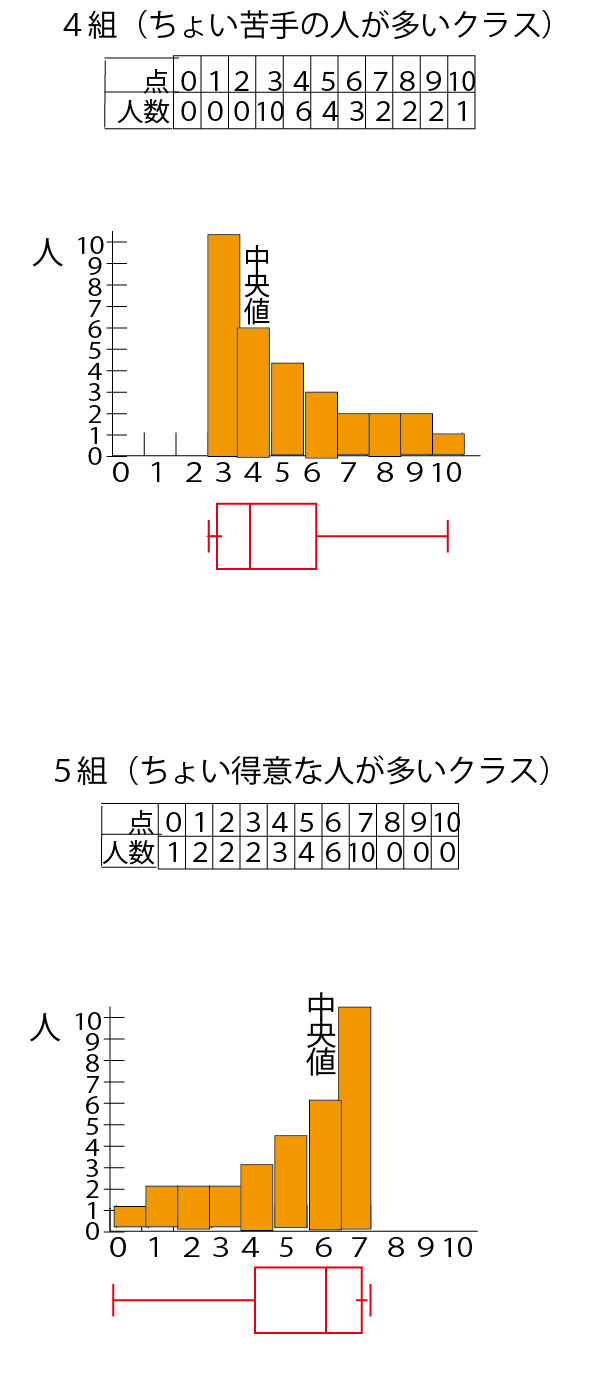
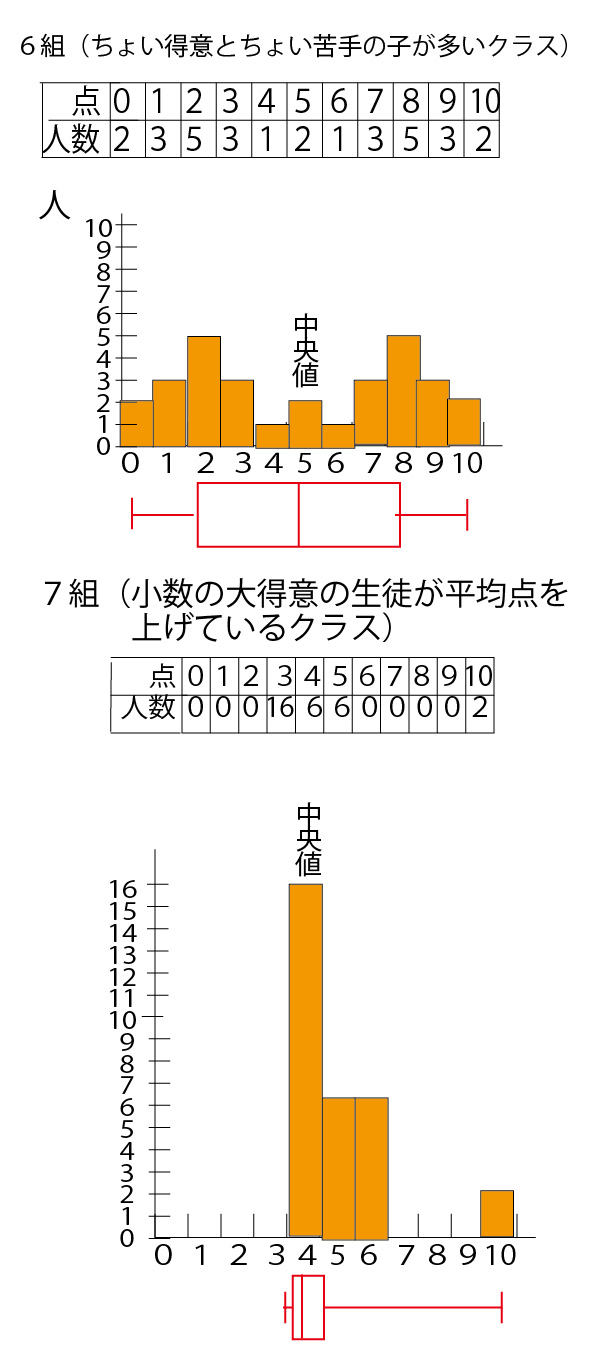
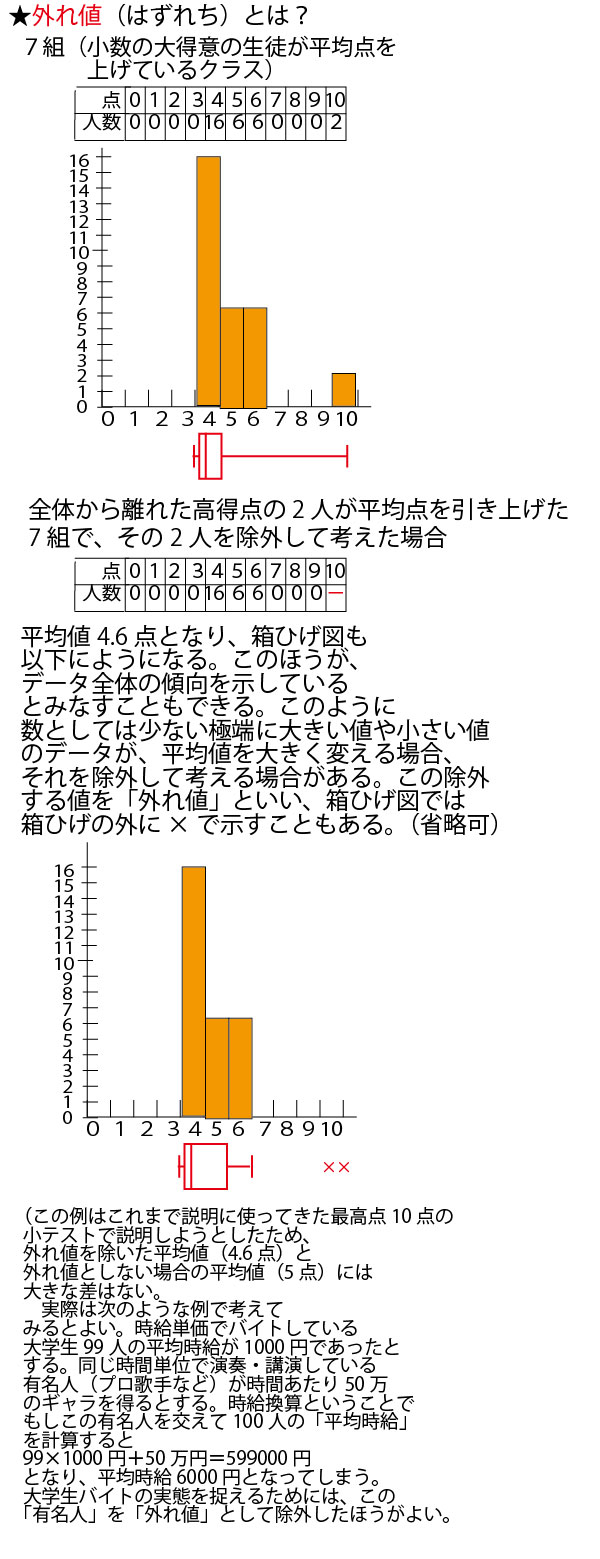

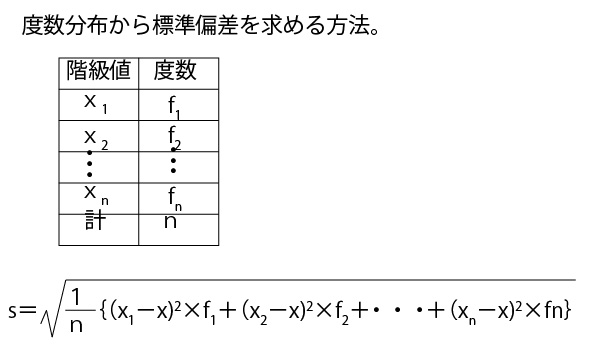
分散・標準偏差に関しては、最初に考えるのは30人クラスでは大きすぎて考えにくいので、まずは、平均点がいずれも5点となる5人組の5班(1班~5班)を例に考えていこう。





●関連大学入試共通テスト・センター試験解答解説
●2021年大学入試共通テスト「数学IA」第1問[1](因数分解・2次方程式の解の公式など)(配点10点)問題・解答・解説