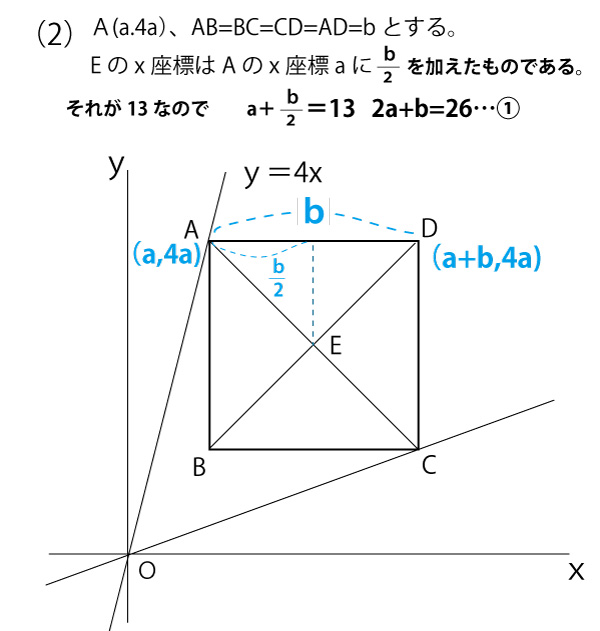
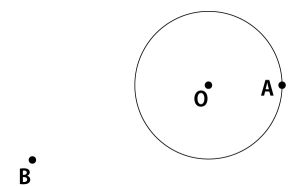
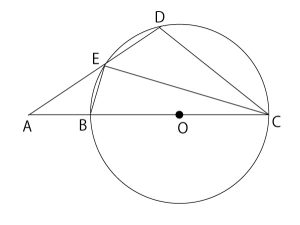
2023年千葉県公立高校入試「数学」第2問（一次関数）（配点15点）問題・解答・解説

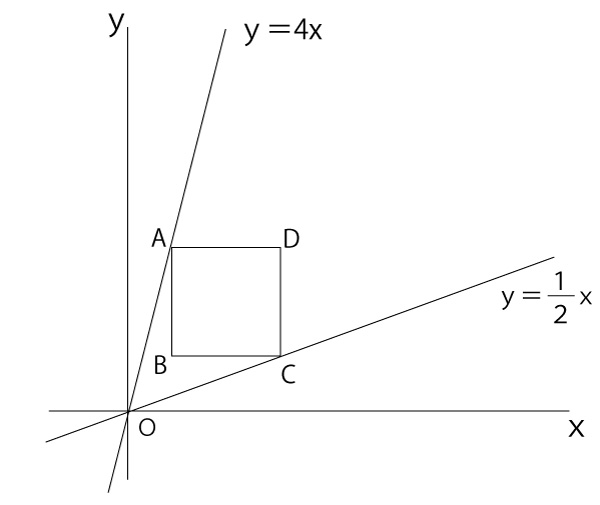
【解説】
（1）Aはy=4x上にある点なので、8＝4x、 x=2

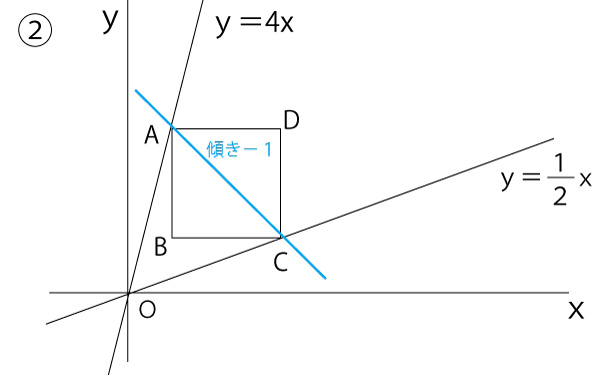
直線ACの傾きは−1で、A（2.8)を通る。
直線AC：y=−x＋bに（2.8)を代入して8=−2＋b、b=10
よってAC：ｙ＝−x+10

（注）（1）に引きずられてＡ（2.8)と考えると、どう考えても、Ｅのｘ座標は13になりえない。（1）と（2）は別問題なので、「点Ａのｙ座標が８である」という（1）の1文目に書かれた条件は（2）では当てはまらない、つまりわからないので、上記のように（a,4a)と置いた。

●Aを（a,4a)、AB＝BC＝CD＝DA＝ｂとして、a,bの連立方程式を解くという発想を思いつく経過

数学の問題は前問が後問のヒントとなっている場合が多い。この問題で、（1）を解く発想が（2)を解くヒントになる可能性が高い。（1）

でＡの座標を求めさせたということはＡの座標に注目したほうがいいというヒントである。また、正方形の4辺の長さが等しく、その長さが、ＡとＤを比較した時のｘ座標の差であることを考えれば、正方形の1辺の長さにも注目したほうがよい。その２つをa、bとすれば、それを解く連立方程式ができそうだと予測する。千葉県の中3（受験生）の正答率がわずか4.4%の問題なので、できなくても気にしなくてもよいが、解ける人の発想は以上のようなものとなる。（なおこの設定の方法の他にも解法はありうる。）