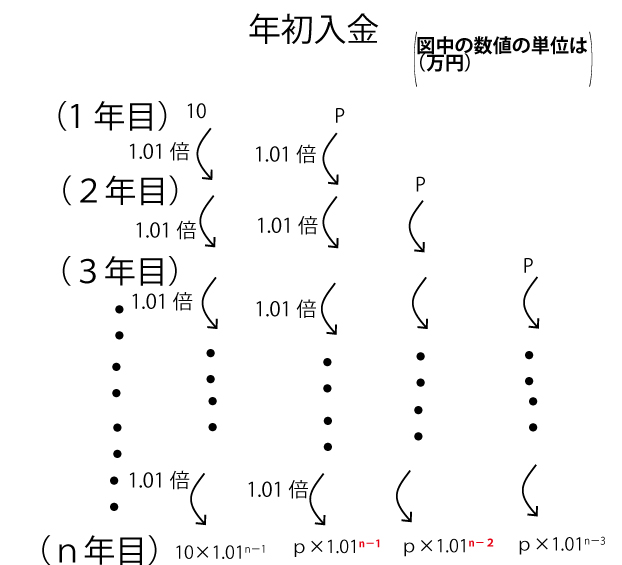
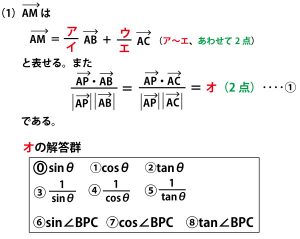
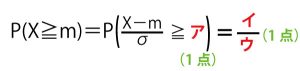2023年大学入試共通テスト「数ⅡＢ」第4問「数列」（配点20点）問題・解答・解説

【解説】

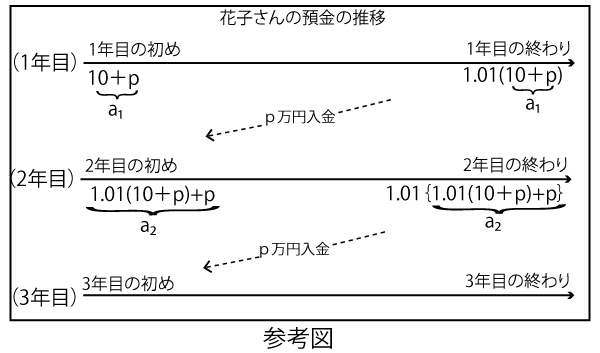
a₃（3年目の初め）は、2年目の終わりの1,01｛1.01（10+p)＋p｝にｐが加わるので
a₃＝1,01｛1.01（10+p)＋p｝＋p（ア答、2点）

前年初めの預金に1年かけて1.01倍になり、その年の初めにp円預金を加えるので、

a_n+1＝1.01a_n＋p （イ答、ウ答、あわせて3点）

a_n+1＋ｂ＝1.01（a_n＋b)とすると
a_n+1＝1.01a_n＋1.01b−b
a_n+1＝1.01a_n＋0.01b

よってｐ＝0.01b
b=100p
代入すると
a_n+1＋100p＝1.01（a_n＋100p)（エ答、オ答、あわせて3点）

方針２

1年目年初入金のｐ万円はn年目年初まで（n年間ではなく）ｎー１年間、預金するため1.01^n－1倍になる。
2年目年初入金のp万円はn年目年初まで,n－2年間、預金するため、1.01^n－2倍になる。
（よって、カ答、キ答、あわせて2点）

（3）
10年目の終わりには、10年目年初の預金額a₁₀が1年間で利息が付き1.01倍となり、11年目年初のp万円は未入金なので
1.01a₁₀であり_、よって1.01a_10（コ答、2点）≧30

前問より

a_n＝10×1.01^n－1＋p・100（1.01ⁿ－1）

a₁₀＝10×1.01⁹＋p・100（1.01¹⁰－1）

1.01a₁₀≧30より
1.01｛10×1.01⁹＋100ｐ（1.01¹⁰−1)｝≧30

（3）最初の設定に加えて3万円分が加わっているので、以下のようにその3万円の利息での増加する分を含めた部分が、多くなる。よって、3×1.01^n－1万（ソ答、2点）円多くなる。