2023年大学入試共通テスト「数ⅡＢ」第3問「確率分布」問題（配点20点）・解答・解説

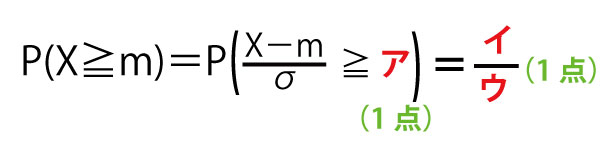
2024年1月12日 2024年1月12日

asakura

2024年1月12日　予備校講師・船橋市議　朝倉幹晴

2023年大学入試共通テスト「数学ⅡB」第3問（配点20点）の解答・解説を作成しましたので、ご活用ください。問題文の最後の所でページ番号「２」をクリックすると解答・解説に飛びます。

2023年のⅡBの他の問題の解答解説は以下の通りです。

2023年のⅠAの問題の解答解説は以下です。

2023年大学入試共通テスト「数学ⅡB」第3問「確率分布」（配点20点）

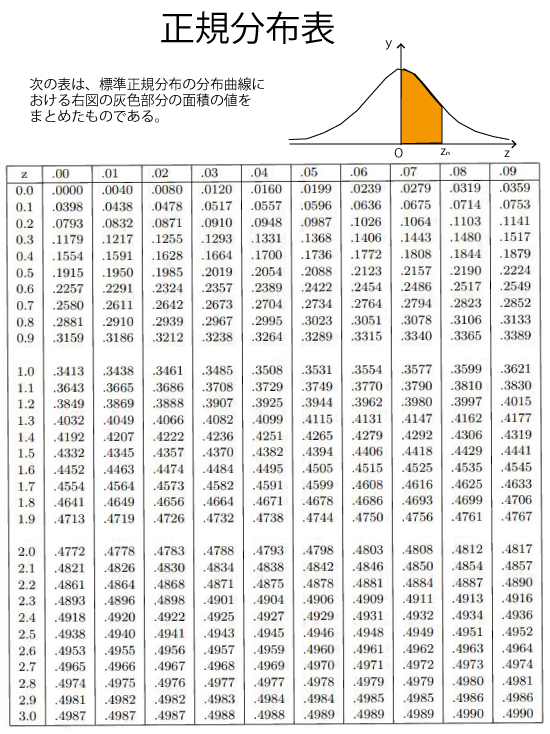
以下の問題を解答するにあたっては、必要に応じて正規分布表（問題文最後に添付）を用いてもよい。

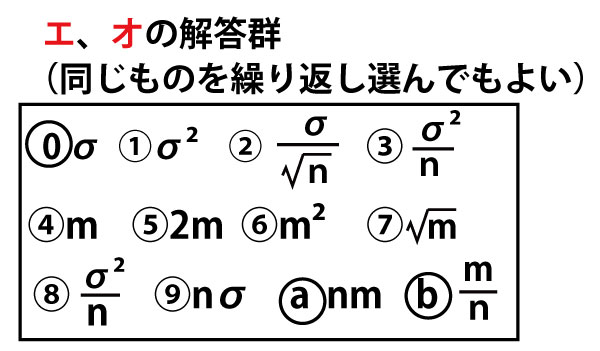
（1）ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ（単位はg）を表す確率変数をXとする。ｍとσを正の実数とし、Ｘは正規分布Ｎ（m、σ²）に従うとする。
（ⅰ）この母集団から1個のピーマンを無作為に抽出したとき、重さがｍｇ以上である確率Ｐ（X≧ｍ）は

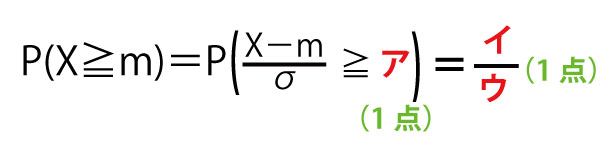
である。

ｎ＝400、標本平均が30.0g、標本の標準偏差が3.6gのとき、ｍの信頼度90％の信頼区間を次の方針で求めよう。

方針
Ｚを標準正規分布Ｎ（0,1)に従う確率変数として、Ｐ（－Z₀≦Ｚ≦Ｚ_o)＝0.901となるZ₀を正規分布表から求める。このＺ_oを用いるとｍの信頼度90.1%の信頼区間が求められるが、これを信頼度90％の信頼区間とみなして考える。

方針において、z₀＝カ.キクである。

一般に、標本の大きさｎが大きいときには、母標準偏差の代わりに、標本の標準偏差を用いてよいことが知られている。ｎ＝400は十分に大きいので、方針に基づくと、ｍの信頼度90％の信頼区間はケとなる。

（2）（1)の確率変数Xにおいて、ｍ＝30.0、σ＝3.6とした母集団から無作為にピーマンを1個ずつ抽出し、ピーマン2個を1組にしたものを袋に入れていく。このようにしてピーマン2個を１組にしたものを25袋作る。その際、１袋ずつの重さの分散を小さくするために、次のピーマン分類法を考える。

ピーマン分類法
無作為に抽出したいくつかのピーマンについて、重さが30.0g以下のときをＳサイズ、30.0gを超えるときはＬサイズと分類する。そして、分類されたピーマンからＳサイズとＬサイズのピーマンを一つずつ選び、ピーマン2個を1組とした袋を作る。

（1）ピーマンを無作為に50個抽出したとき、ピーマン分類法で25袋作ることができる確率p₀を考えよう。無作為に1個抽出したピーマンがＳサイズである確率はである。ピーマンを無作為に50個抽出したときのＳサイズのピーマンの個数をＵ₀とすると、Ｕ₀は二項分布

に従うので

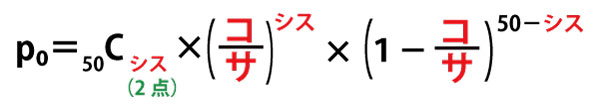
となる。
p₀を計算すると、p_o＝0.1122…となることから、ピーマンを無作為に50個抽出したとき、25袋作ることができる確率は0.11程度とわかる。

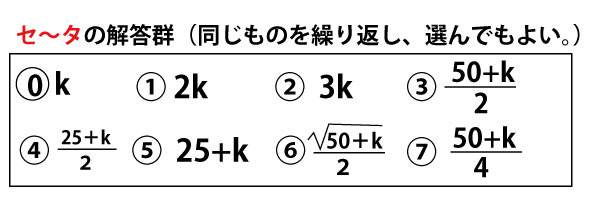
（ⅱ）ピーマン分類法で25袋作ることができる確率が0.95以上となるようなピーマンの個数を考えよう。
ｋを自然数とし、ピーマンを無作為に（50＋k)個抽出したとき、Ｓサイズのピーマンの個数を表す確率変数をＵ_kとすると、Ｕ_kは二項分布

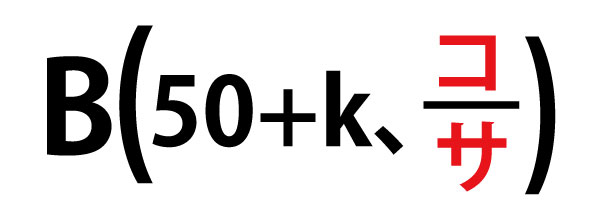
に従う。

（50＋ｋ）は十分に大きいので、Ｕ_kは近似的に正規分布Ｎ（セ、ソ）に従い、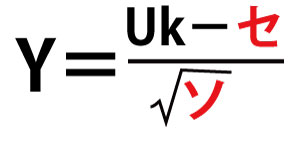とすると、Ｙは近似的に標準正規分布Ｎ（0,1)に従う。

したがって、少なくとも（50＋チツ）個のピーマンを抽出しておけば、ピーマン分類法で25袋作ることができる確率は0.95以上となる。

[next_p]