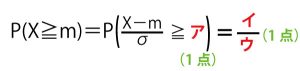2023年大学入試共通テスト「数ⅡB」第4問「数列」(配点20点)問題・解答・解説
2024年1月11日 予備校講師・船橋市議 朝倉幹晴
2023年大学入試共通テスト「数学ⅡB」第4問(配点20点)の解答・解説を作成しましたので、ご活用ください。問題文の最後の所でページ番号「2」をクリックすると解答・解説に飛びます。
ⅡBの解答解説は順次作成中ですが、IAは完成していますのでご活用ください。
2023年大学入試共通テスト数学ⅡB第1問[1](配点18点)問題・解答・解説
2023年大学入試共通テスト「数ⅡB」第1問[2](配点12点)問題・解答・解説
2023年大学入試共通テスト「数ⅡB」第2問[1](配点15点)問題・解答・解説
2023年大学入試共通テスト「数ⅡB」第2問[2](配点15点)問題・解答・解説
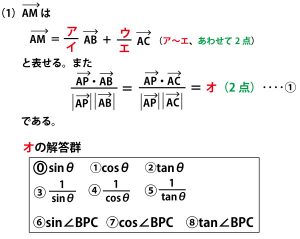
2023年大学入試共通テスト「数ⅡB」第5問「ベクトル」(配点20点)問題・解答・解説
2023年大学入試共通テスト「数学ⅡB」第4問「数列」(配点20点)
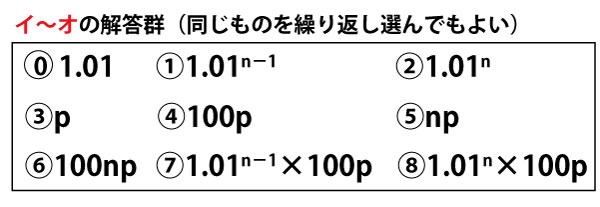
花子さんは、毎年の初めに預金口座に一定額の入金をすることにした。この入金を始める前における花子さんの預金は10万円である。ここで、預金とは預金口座にあるお金の額のことである。預金には年利1%で利息がつき、ある年の初めの預金がx万円であれば、その年の終わりには預金は1.01x万円となる。次の年の初めには1.01x万円に入金額を加えたものが預金となる。
毎年の初めの入金額をp万円とし、n年目の初めの預金をan万円とおく。ただし、p>0とし、nは自然数とする。例えば、a1=10+p、a2=1.01(10+p)+pである。

(1)anを求めるために二つの方針で考える。
方針1
n年目の初めの預金と(n+1)年目の初めの預金との関係に着目して考える。
3年目の初めの預金a3万円について、a3=ア(2点)である。すべての自然数nについて
an+1=イan+ウ(あわせて3点)
が成り立つ。これは
an+1+エ=オ(an+エ)(あわせて3点)
と変形でき、anを求めることができる。

方針2
もともと預金口座にあった10万円と毎年の初めに入金したp万円について、n年目の初めにそれぞれがいくらになるかに着目して考える。
もともと預金口座にあった10万円は、2年目の初めに10×1.01万円になり、3年目の初めに10×1.012万円になる。同様に考えるとn年目の初めには10×1.01n-1万円になる。
・1年目の初めに入金したp万円は、n年目の初めにはp×1.01カ万円になる。
・2年目の初めに入金したp万円は、n年目の初めにはp×1.01キ万円になる。
・n年目の初めに入金したp万円は、n年目の初めにはp万円のままである。
(カキあわせて2点)
(2)花子さんは、10年目の終わりの預金が30万円以上になるための入金額について考えた。
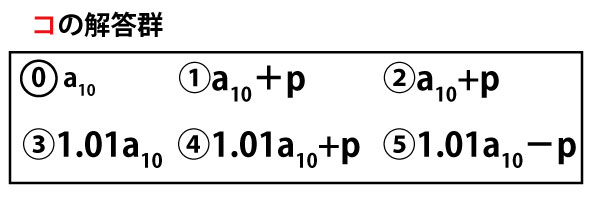
10年目の終わりの預金が30万円以上であることを不等式を用いて表すとコ(2点)≥30となる。この不等式をpについて解くと

となる。したがって、毎年の初めの入金額が例えば18000円であれば、10年目の終わりの預金が30万以上になることがわかる。
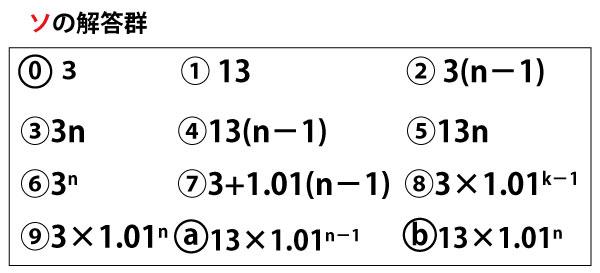
(3)1年目の入金を始める前における花子さんの預金が10万円ではなく、13万円の場合を考える。すべての自然数nに対して、この場合のn年目の初めの預金はan万円よりもソ万円(2点)多い。なお、年利は1%であり、毎年の初めの入金額はp万円のままである。
[next_p]