2018年千葉県公立高校入試(前期)数学第4問(図形の証明)問題・解答・解説(2018年2月13日実施)

船橋市議・予備校講師 朝倉幹晴
【はじめに】私は、様々な理由で受験や進学で不利になっている子どもたち(原発被災避難世帯、児童養護施設、母子生活支援施設、ひとり親家庭など)の学習サポートを続けてまいりました。しかし直接伺える場所・教えられる子どもの数は限られますので、どなたでもご覧いただけるように、公式サイトにその内容をUPすることにいたしました。どうぞご活用ください。
内容は、中学生の皆様に学んでいただける内容であるとともに、保護者の皆さんに、自分のお子さんがどのような問題に挑戦をされているかの内容を知っていただきたいという思いもあります。保護者の皆さんもどうぞご覧ください。
【注意事項】
①前半に問題、後半に解答解説があります。問題にじっくりとりくみ考えたい人は、「以下解答解説です」の画像のところで画面を止める(印刷した場合はそれより下を見ない)ようにしてください。
②入試問題は実際は、白黒です。ただせっかくの画像上ですので、一部カラーにしました。



【解説】
千葉県公立高校入試の第4問【証明】の問題の流れは以下のようになる。特に問題文の最初に証明すべきこと=「目的」が明記してあること。前半の出題者自身が記述している部分の最後が「手段」となり、後半の「目的」の証明の流れの冒頭になることを理解しておくとよい。また「目的」の証明のためには、直接の条件として何が必要かを考えると、記述の部分の最後の目標がはっきりする。

2018年前期のこの問題では以下のように考えられる。

★証明前半の理解と空欄(a)(b)の答
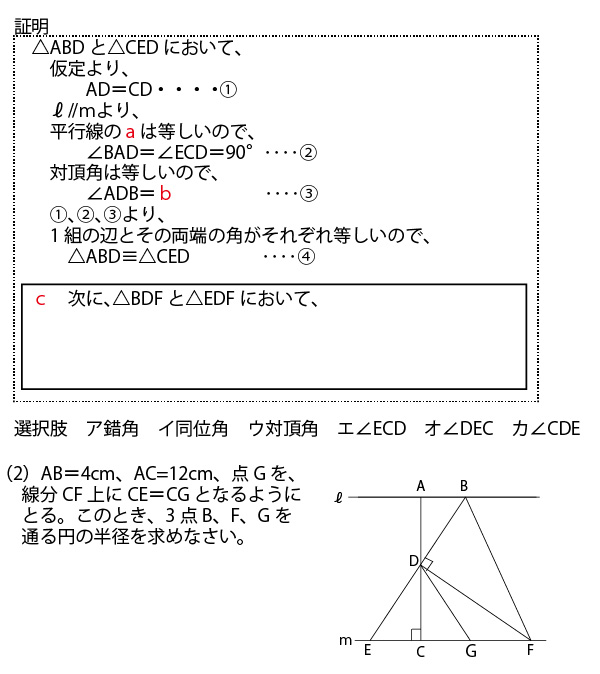
まず、問題文に書いてある証明の前半の流れを理解しながら、空欄(a)(b)を考えよう。証明冒頭に「△ABDと△CEDにおいて」と示されているし、前半の最後(後半のために使う「手段」の関係)に「△ABD≡△CED」と書いてあるので、この2つの三角形に注目しよう(以下画像では灰色に塗っているが、実際の入試では鉛筆書きの斜線で示すとよい)。
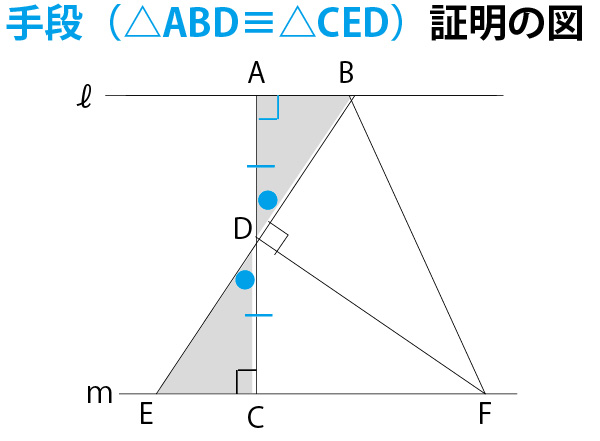
図の青線・青●に注目すると、空欄(a)(b)は次のようになる。

さて次の後半の(c)の流れを考えると以下のようになる。目的である二等辺三角形であることの証明のためには、「2辺が等しい」か「2底角が等しい」ということをしめせばよい。後半(c空欄前)の冒頭が「△BDFと△EDF」への注目を示唆している。△BDF≡△EDFを示すことでBF=EFを示すことができることを示唆してくれている。
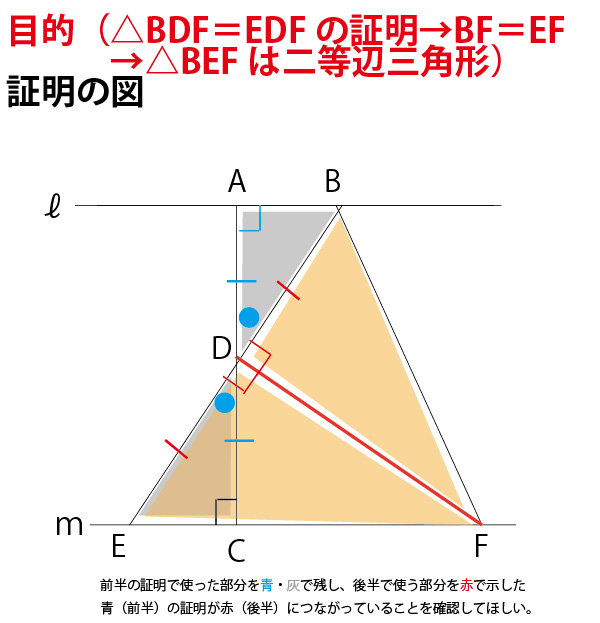
上図の赤で示した部分を骨格に文章化し、上図のオレンジで示した2つの三角形が合同であることを示しながら、以下のように目的(△BEFが二等辺三角形)までいたる文章を作っていく。

さて、最後の数値を求める問題(2)を考えていこう。もちろん(1)(証明)でわかったことを活用していく。
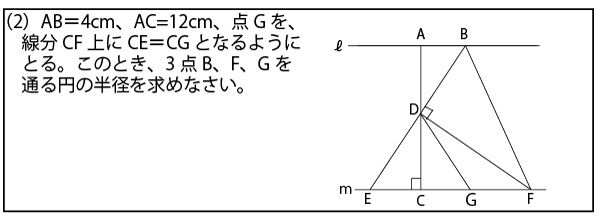
まず、図の中に直角三角形が存在し、また円を描くという事実から考えて以下の「タレスの定理」を活用して解くのではないかと予測する。(千葉県の公立高校入試の「図形の証明」の問題では「タレスの定理」を活用する問題の出題頻度が高い。)
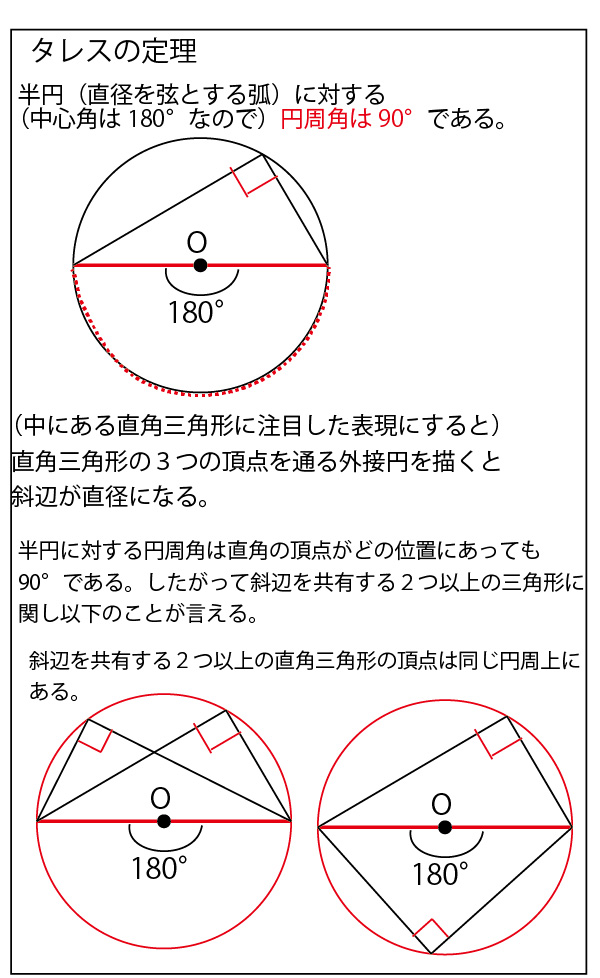
まず外接円を描くと指定された点B、G、Fを結ぶ三角形は、図から考えて
∠BGF=90°の三角形となり、タレスの定理が使えることになるのではないかと予測し、それを証明してみる。(証明の文章までは要求されていないので理解できればよい)。以下の図で考えてみよう。
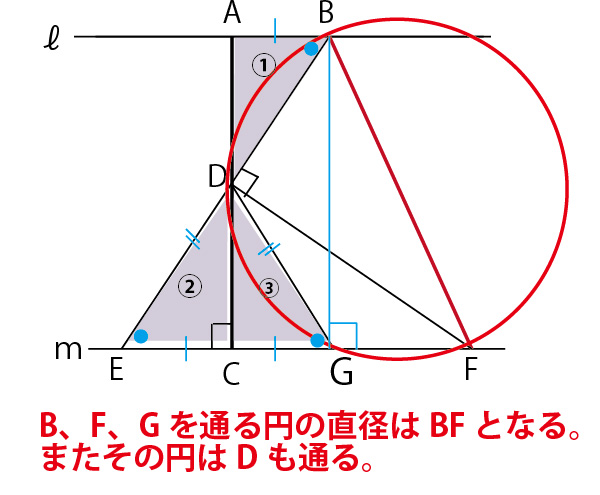
前問で図の中の①と②の三角形が合同であることは証明されている。図の青字で示したように、条件よりDE=DG、そして二等辺三角形の底角は等しい(図の青●)ので、
∠DEC=∠DGC。すると斜辺と1つの鋭角が等しい直角三角形なので、②と③も合同。すると①と③も合同なのでAB=CG。四角形ACGBは長方形なので、AC∥BG。よって∠BGF=90°。よってタレスの定理より、BFは直径となる。
また斜辺を共有する2つ以上の直角三角形の頂点は同じ円周上にあるから、
Dもこの円周上となる。(仮に証明はできなくても、図を描けば、Dは円周上にありそうだとは予測できる。)
したがって、直径BFの長さを求めれば、その半分が円の半径となる。
まずは直角三角形△BFGで三平方の定理を使いたいが、GFの長さが不明で使うことはできない。そこで斜辺をBFとするもう1つの直角三角形△BDFで三平方の定理を使うことを考える。
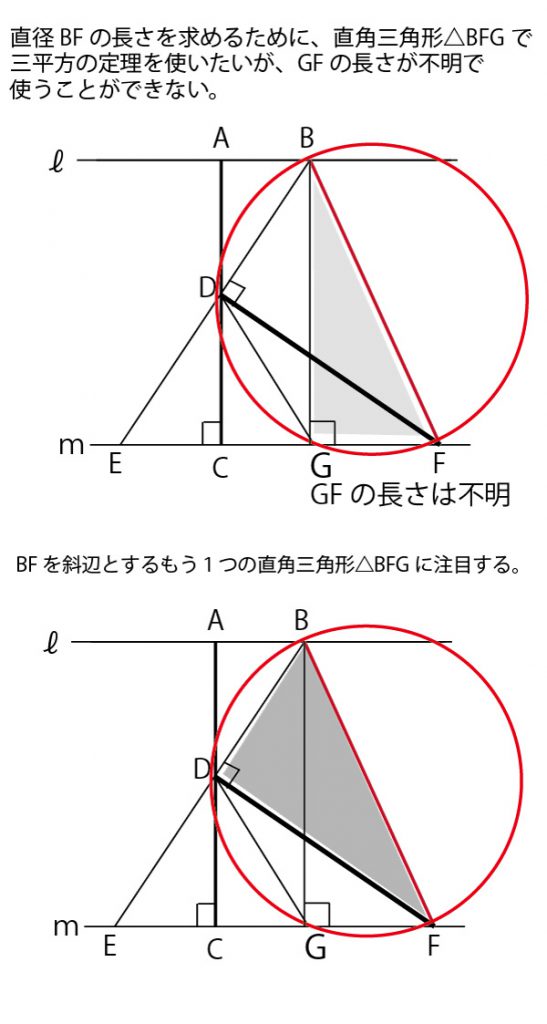
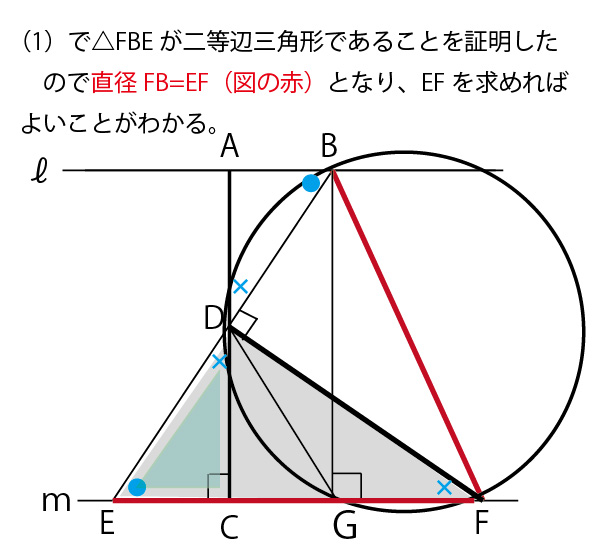
(1)で証明しうたように△FBEは二等辺三角形なのでFB=EF。よって直径FBの長さを求めるためには
EFを求めればよいことがわかる。
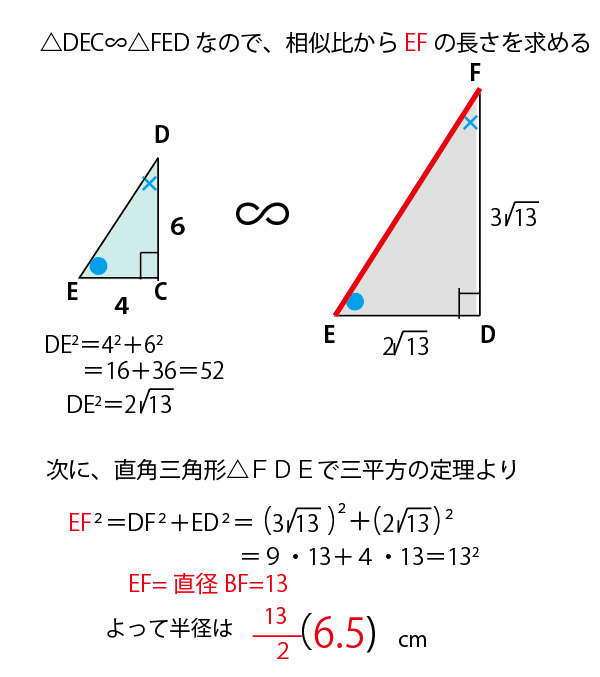
直角三角形では、直角以外の2つの鋭角の和が90°なので、それを下図のように「●+×=90°」であることを使って、考えていくと、△DEC∽△FEDとわかり、相似比から、FDの長さがわかり、直角三角形△BDFで三平方の定理からEFを求めることができる。
★参考 拙著「図形の証明」(他3著作)、アマゾンでお求めいただけます。