2012年前期、千葉県公立高校入試「数学」第5問「図形の証明」（配点計14点）問題・解答・解説

2021年7月24日（土）午前11時　予備校講師・船橋市議　朝倉幹晴

2012年2月の千葉県公立高校入試「数学」の第5問「図形の証明」の問題・解答、そして私（朝倉幹晴）が作成した解説です。千葉県教育委員会が発表した各小問の正答率（無答率）も付記しました。ご活用ください。

2012年前期数学第5問「図形の証明」（配点14点）

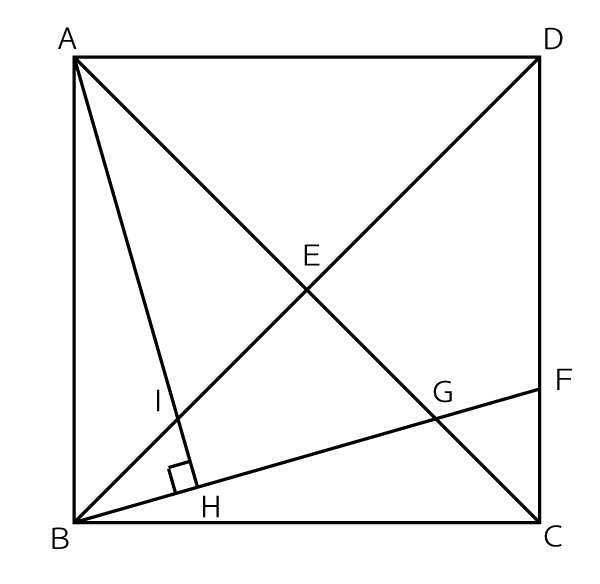
図の正方形ＡＢＣＤにおいて、２つの対角線の交点をＥとする。辺ＣＤ上に2点Ｃ、Ｄと異なる点Ｆをとり、線分ＢＦと線分ＡＣとの交点をＧとする。
また点Ａから線分ＢＦに垂線ＡＨをひき、線分ＡＨと線分ＢＤとの交点をＩとする。
このとき、次の（1）～（3）の問いに答えなさい。

（１）ＡＩ＝ＢＧであることを、次の□の考えにしたがって証明するとき、aとb（両方正解で2点、.順不同、正答率71.6%（無答率4.0%))に入る最も適当なものを、選択肢のア～エのうちからそれぞれ一つずつ選び、符号で答えなさい。また、ｃ（2点、正答率59.8%（無答率7.3%))に入る最も適当なことばを書きなさい。

AI＝BGであることを証明するためには、aとbがcであることを証明すればよい。

選択肢　　ア△ＡＢＩ　イ△ＡＩＥ　ウ△ＡＢＧ　エ△ＢＧＥ

（2）（1）の□の考えにしたがって、AI=BGであることを証明しなさい。（6点、6点評価4.4%、部分点（3点）3.5%（無答率51.5%))
（3）BH=2cm、HG＝3cmとなるとき、正方形ABCDの面積を求めなさい。(4点、正答率1.1%（無答率53.4%))

[next_p]