2012年前期、千葉県公立高校入試「数学」第4問「二次関数」（配点計10点）問題・解答・解説

2021年7月24日（土）午前8時　予備校講師・船橋市議　朝倉幹晴

2012年2月の千葉県公立高校入試「数学」の第4問「二次関数」の問題・解答、そして私（朝倉幹晴）が作成した解説です。千葉県教育委員会が発表した各小問の正答率（無答率）も付記しました。ご活用ください。

2012年前期数学第4問「二次関数」（配点10点）

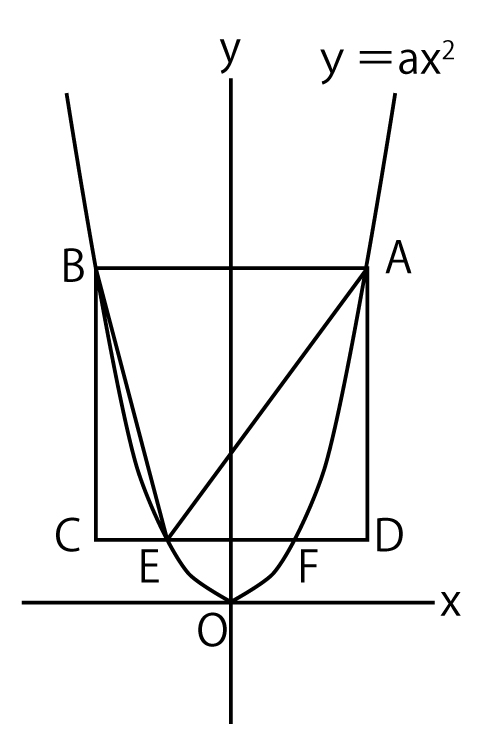
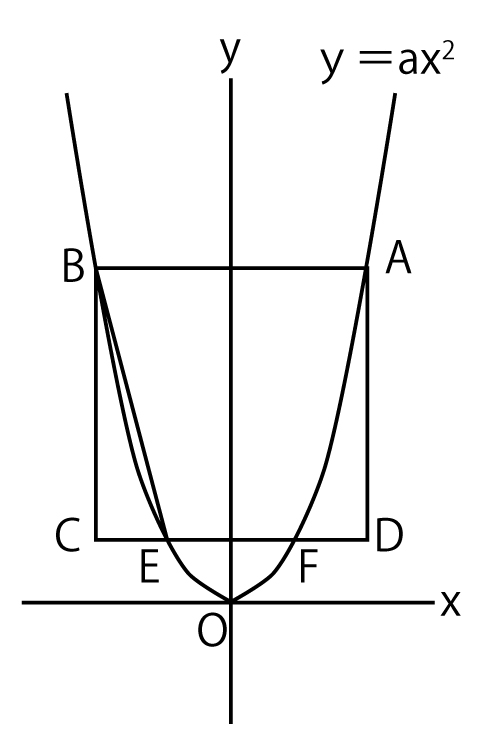
図のように、関数y＝ax²のグラフ上に、ｘ座標が4,ｙ座標が正となる点Aがある。点Aとｙ軸について線対称な点Bをとり、線分ABを一辺とする正方形ABCDをかいたところ、線分CDは関数ｙ＝ax²のグラフと異なる2点E・Fで交わり、CD：EF＝２：１となった。ただし、点C・Eのｘ座標は負とする。

このとき、次の（1）（2）の問いに答えなさい。

（1）aの値を求めなさい。（5点配点）（正答率13.5%（無答率26.6%))
（2）ｙ軸上に点Pをとる。△ABEと△APEの面積が等しくなるとき、点Pの座標を求めなさい。ただし、点Pのｙ座標は、点Aのｙ座標より大きいものとする。
  （5点配点）（正答率6.2%（無答率53.4%))

[next_p]