2012年前期、千葉県公立高校入試「数学」第4問「二次関数」（配点計10点）問題・解答・解説

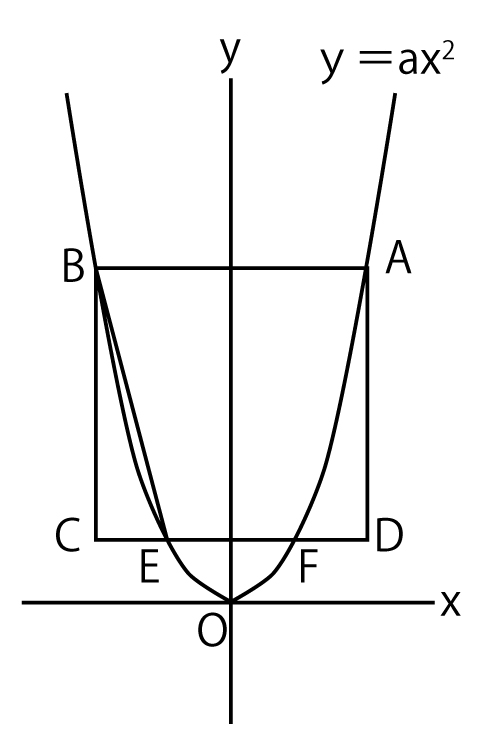
【解説】

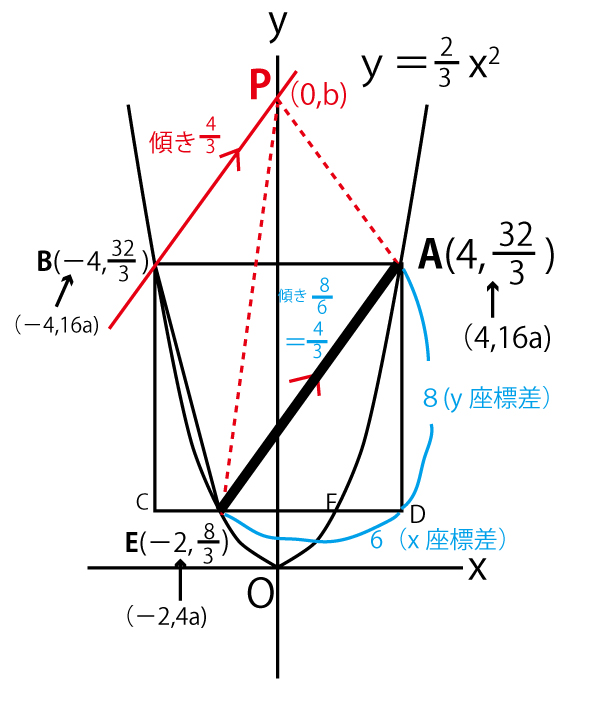
（1）Aは、y＝ax²のグラフ上でｘ座標が4の点なので、y座標はy=a×4²＝16a。A（4、16a)。点Aとｙ軸について線対称な点Bは（－4、16a)
よってABの長さはｘ座標の差で４ー（－4）＝８。
ＡＢＣＤは正方形なのでAD=8、BC=8で、座標はD(4,16aー8)、C(－4、16aー8)。

一方、CD：EF＝２：１で、EとFはy軸に対して線対称な点なので、それぞれのｘ座標は２と－２であり、ｙ座標はｙ＝a×2²=４a、ｙ＝a×（－2)²=４a。
なので、座標はE（2,4a）F（－2,4a)
D,C,E,Fはx軸と平行な線CD上にある点なので両者のy座標は同じなので、
16a－8＝4a
12a=8
3a=2

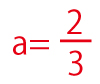
（2）
前問で求めた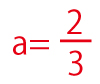の値を代入し、各点の座標を書き込む。

△ABEの面積＝△APEの面積となるためには、
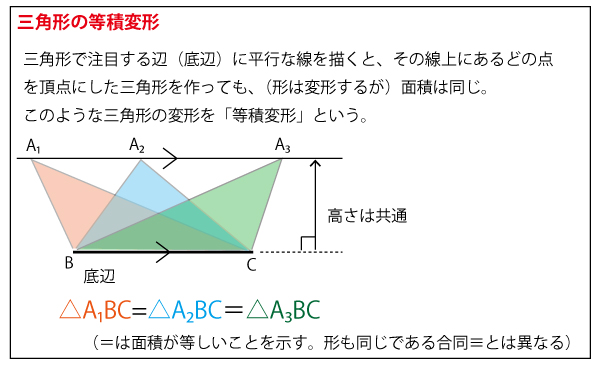
（図形の式で≡は合同を示し、＝は面積が等しいことを示すので、単に「△ABE＝△APE」と表記してもよい）
底辺EA（図の太線）は共通なので、それに対する高さが同じになればよい。Bを通りEAに平行な線（図の赤線）を引き、その線上に点をとると、その点とE、Aを3頂点とする三角形は△ABEと同じ体積となる。これを三角形の形は変わっても面積が同じとなるので「等積変形（の三角形）」という。Pもこの線上にあるはずである。