2012年前期、千葉県公立高校入試「数学」第5問「図形の証明」(配点計14点)問題・解答・解説
【解答】
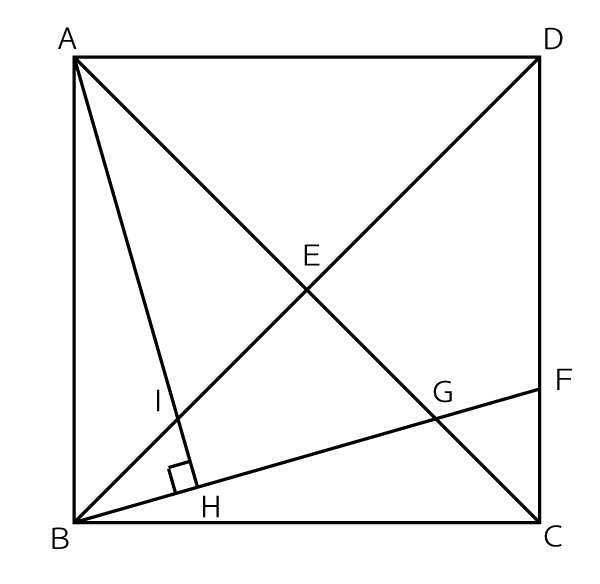
(1)a・b イ(△AIE)・エ(△BGE) (両方正解で2点、.順不同、正答率71.6%(無答率4.0%))
c合同(2点、正答率59.8%(無答率7.3%))
(6点、6点評価4.4%、部分点(3点)3.5%(無答率51.5%))
(3)40(cm3)(4点、正答率1.1%(無答率53.4%))
【解説】
(1)角度が等しいことならば「相似」でも証明できるが、AI=BGは線分の長さが等しいことなので、三角形の「合同」を証明し、対応する辺であることを示す証明であると予測できる。
選択肢の4つの3角形ではア(△ABI)とウ(△ABG)は明らかに形が他と異なる。イ(△AIE)とエ(△BGE)は直角三角形で形も同じで、この合同を証明することと推測できる。
(2)
(1)で合同を証明すべきと決めた三角形について、図の赤字で書いたように、1つの角(直角)と1辺が等しいことはすぐわかる。
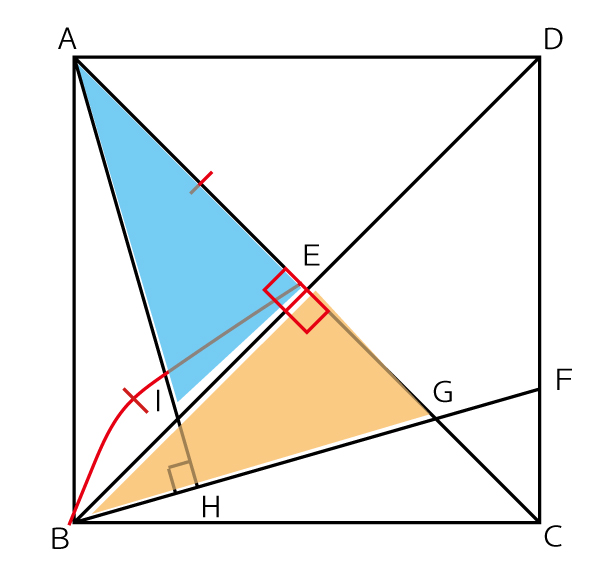
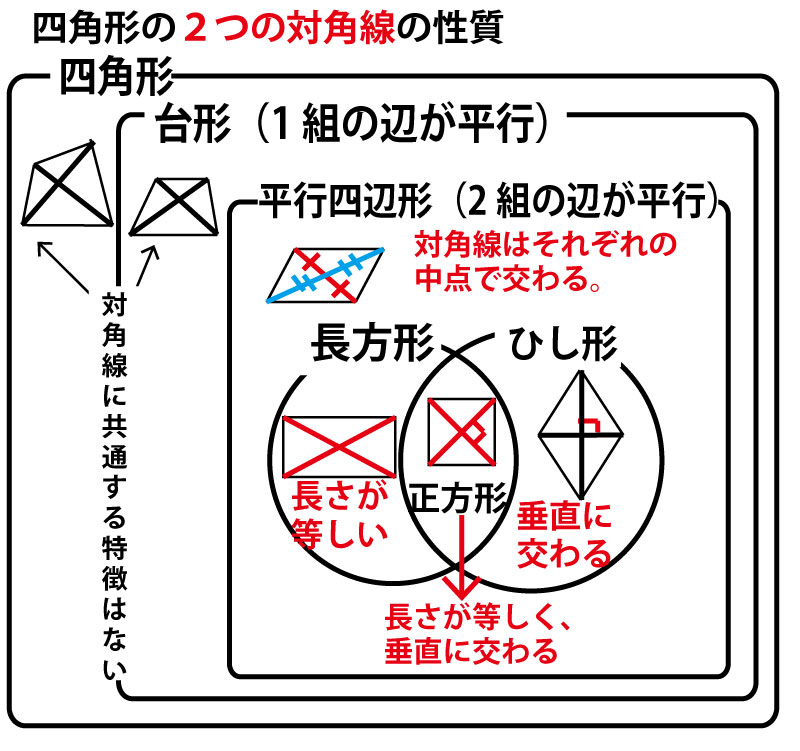
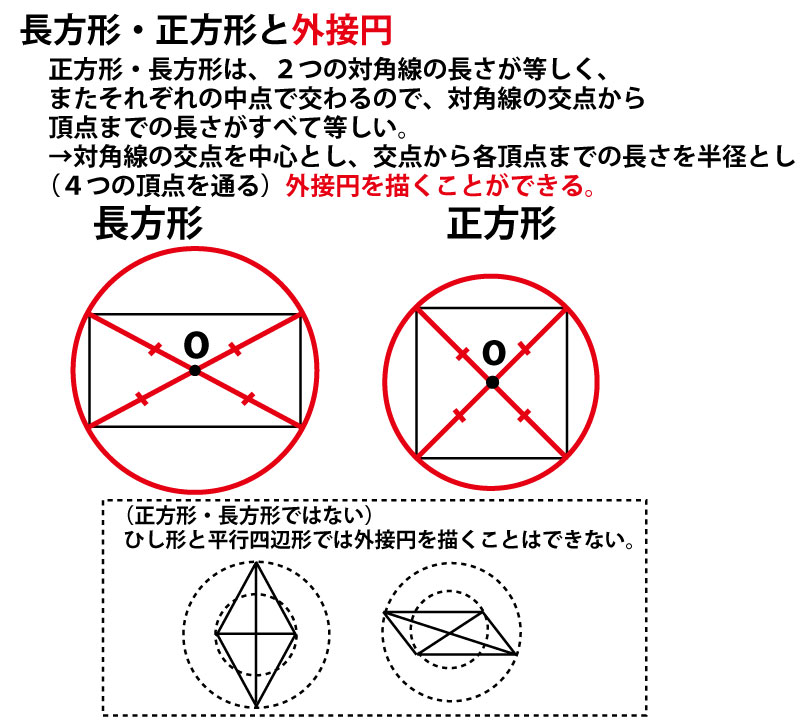
(四角形の対角線の性質については末尾にまとめを添付したので確認してほしい。)
しかしもう1つの条件が出てこない。
合同条件「2辺とその間の角」を使うためには、IE=EGの証明が必要であるが、証明できる要素がない。
合同条件「1辺とその両端の角」を使うためには、∠IAE=∠GBEが必要で、角が等しい証明ならば、他の相似の三角形に注目すればできそうである。
そこで以下のようにIで対面する△AIEと△BIHに注目する。目的の証明のために、「手段」としてこの三角形の相似を活用するのである。
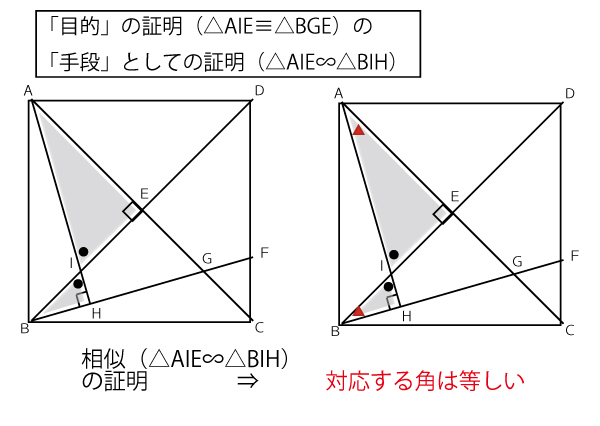
△AIE∽△BIHは、左図に黒で書いたように「2組の角がそれぞれ等しい」で証明できる。
すると残りの対応する角(図の赤▲)も等しいと証明できる。
それをもとに図にはめ込むと、目的の合同の証明の条件(1組の辺とその両端の角がそれぞれ等しい)がそろうことがわかる。
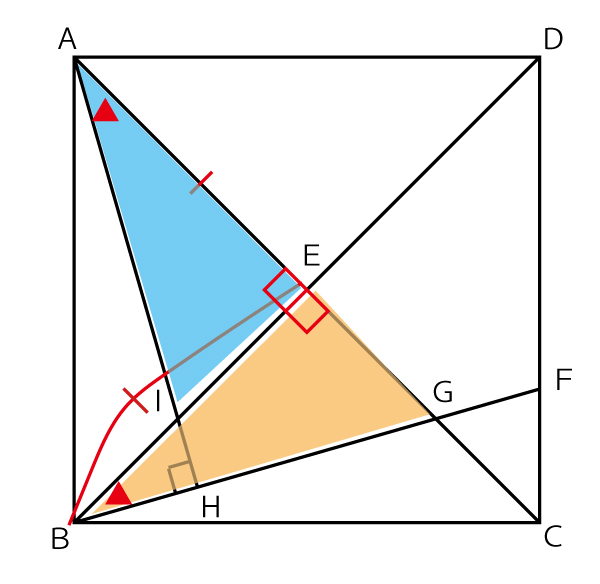
この流れを文章化したものが解答の証明の流れである。つまり証明をきちんと記述するためには、このように図の中で流れを確認していく必要がある。
千葉県公立高校入試ではこの年(2012年前期)では、問題用紙への添付図が1つであったが、2013年前期~2020年前期まで、「手段の図形の証明⇒目的の図形の証明」の「2段階証明」を出題する上で、受験生たちが、書き込んで考えやすいように、図を複数(2つか3つ)問題用紙に描くように改善された。
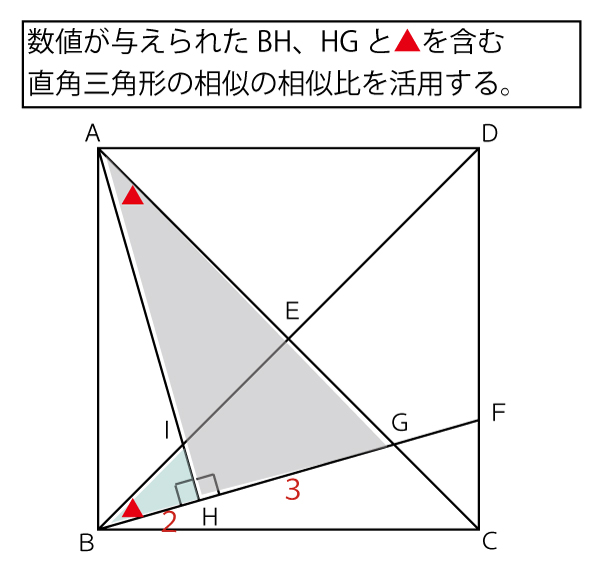
(3)正方形ABCDの面積を求めるには1辺の長さ(AB)がわかればよい。また図中には直角三角形が多数あり、ABの長さを求める問題なので、三平方の定理を計算に使うことが予測できる。また(2)で使った▲を含む直角三角形は合同になるので、今度は、数値が与えられたBHやHGと▲を含む直角三角形を考え相似比を求めてみる。
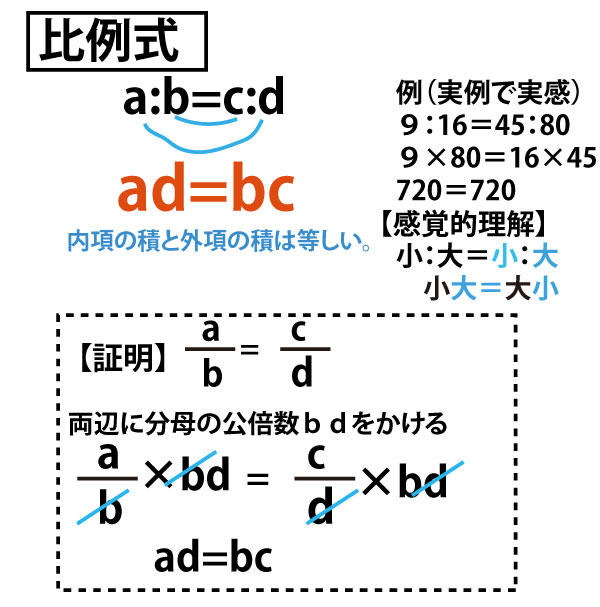
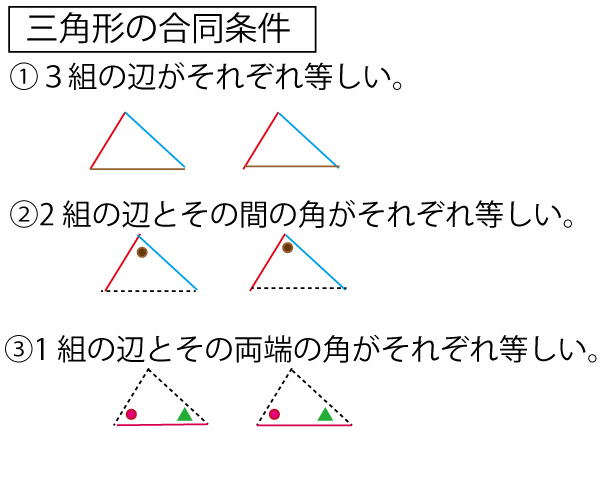
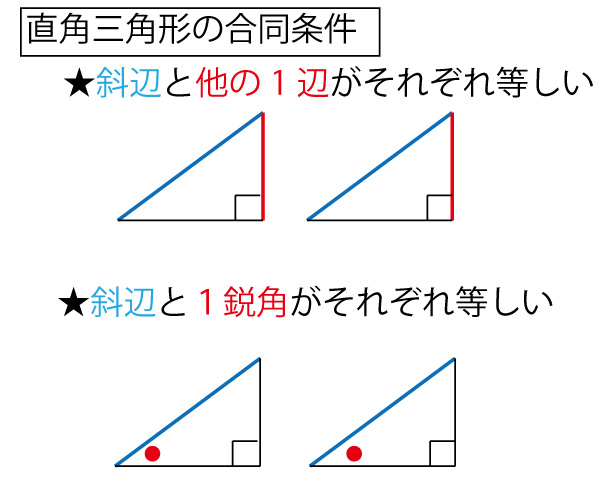
図形に関わる様々なまとめ
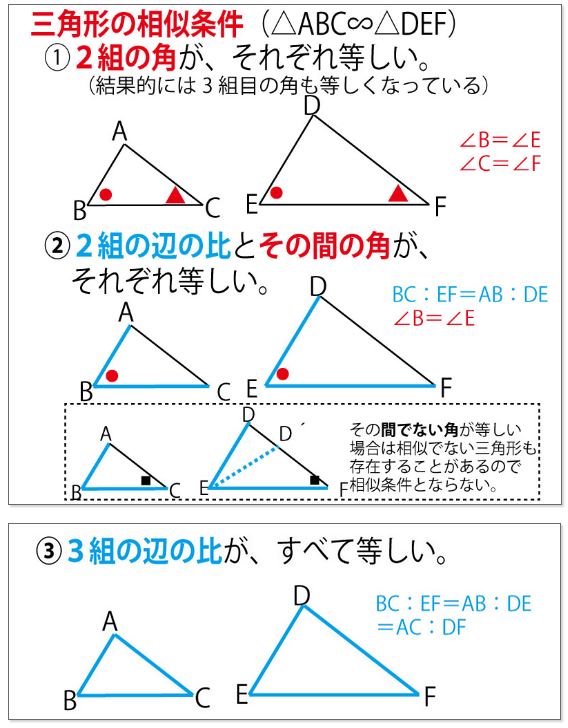
三角形の相似条件を確認しましょう。
★参考 拙著「図形の証明」(他3著作)、アマゾンでお求めいただけます。