2013年前期、千葉県公立高校入試「数学」第5問(図形の証明、配点14点)問題・解答・解説
2021年7月22日 予備校講師・船橋市議 朝倉幹晴
2013年2月の千葉県公立高校入試「数学」の第5問(図形の証明・14点)の問題・解答、そして私(朝倉幹晴)が作成した解説です。千葉県教育委員会が発表した各問の正答率(無答率)も付記しました。ご活用ください。
2013年前期、第5問(配点14点)
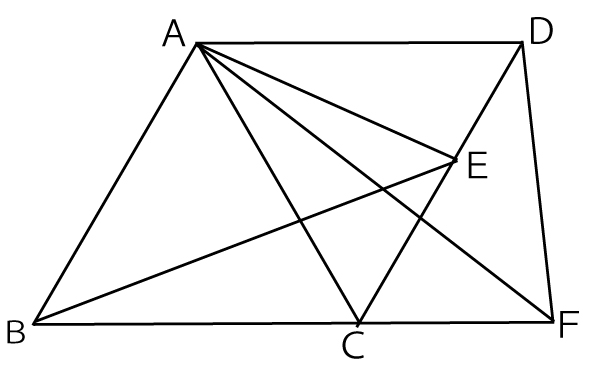
図で、四角形ABCDは、∠ADC=60°のひし形である。辺CD上に2点C、Dと異なる点Eをとり、辺BCの延長線上に点FをCE=CFとなるようにとる。このとき、△ABE≡△DAFとなる。
その証明を下の□の中に途中まで示してある。

証明
2点ACを結ぶ。
仮定から、四角形ABCDの4つの辺は等しく、
∠ABC=∠ADC=60°なので
△ABCと△ACDは正三角形である。…△BCEと△ACFにおいて、
仮定からCE=CF・・・
より、BC=(a)・・・
また、∠BCA=∠ACD=60°なので
∠DCF=180°ー∠BCA-∠ACD=60 °となり
∠BCE=(b)=120°・・・


より (c) ので
△BCE≡△ACF・・・・
(続く)
次の(1)~(3)の問いに答えなさい。
(1)□の中の(a)(b)(両方正解で2点、正答率56.9%(無答率2.0%))に入る最も適当なものを、A群のア~カの中から、
(c)(2点、正答率79.4%(無答率3.9%)に入る適当なものを、B群のア~ウの中から、それぞれ1つずつ選び、符号で答えなさい。
A群 アAC イAD ウAF エ∠AEC オ∠ACF カ∠BAD
B群
ア 3辺がそれぞれ等しい
イ 2辺とその間の角がそれぞれ等しい
ウ 1辺とその両端の角がそれぞれ等しい
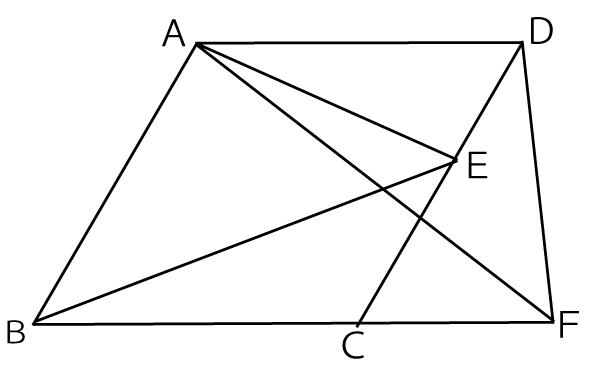
(2)□の中の証明の続きを書き、証明を完成させなさい。ただし、□の中の ~
~ に示されている関係を使う場合、番号の
に示されている関係を使う場合、番号の ~
~ を用いてよい。
を用いてよい。
(6点)(完全正答率(6点)8.7%、部分点(3点)4.6%(無答率54.0%))
(3)AB=10cm,CE:ED=3:2のとき、AEの長さを求めなさい。(4点)(正答率3.0%(無答率39.7%))
[next_p]