2013年前期、千葉県公立高校入試「数学」第4問（総合問題、配点16点）問題・解答・解説

2021年7月21日　予備校講師・船橋市議　朝倉幹晴

2013年2月の千葉県公立高校入試「数学」の第4問（総合問題・16点）の問題・解答、そして私（朝倉幹晴）が作成した解説です。千葉県教育委員会が発表した各問の正答率（無答率）も付記しました。ご活用ください。

図１のように、対角線の長さが40cmの正方形の形をした画面～がある。これら３つの画面には、スイッチ（スタートボタン）を入れると、それぞれ色のついた図形（図の色部分）が映し出され
時間の経過に伴ってその大きさや位置が変化する。

次の（1）～（3）の問いに答えなさい。

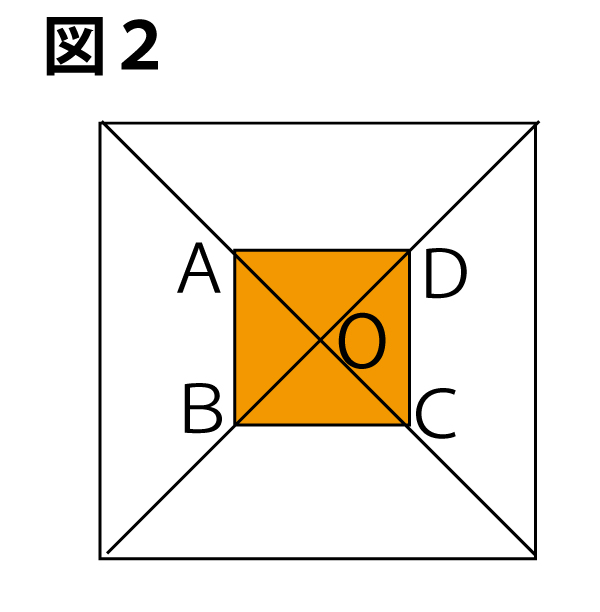
（1）画面では、スイッチを入れると、図2のように、正方形ＡＢＣＤの各頂点が、両面の対角線の交点Ｏを出発し、それぞれ四隅（すみ）に向かって対角線上を毎秒１cmの速さで移動
する。スイッチを入れてからｘ秒後の正方形ＡＢＣＤで囲まれた灰色部分の面積をｙcm²とする時、ｙをｘの式で表しなさい。ただし０＜ｘ≦20とする。（4点）（正答率24.7%（無答率26.0%))

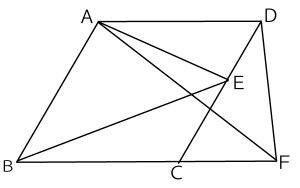
（2）画面では、スイッチを入れると図3のように正方形ＡＢＣＤの各頂点が、（1）と同じ条件で移動し、更に、スイッチを入れてから２秒後に正方形ＰＱＲＳの各頂点が、画面の対角線の交点
Ｏを出発し、それぞれ四隅に向かって対角線上を毎秒1cmの速さで移動する。
スイッチを入れてからｘ秒後の正方形ＡＢＣＤと正方形ＰＱＲＳで囲まれた色部分の面積をｙcm2とするとき、ｙをｘの式で表しなさい。ただし、２＜ｘ≦20とする。
（4点）(正答率6.9%(無答率51.3％））

（3) 画面では、スイッチを入れると画面の対角線で区切られた図４で、の部分は次の規則に従って、それぞれ色がついたり、消えたりする。スイッチを入れてからの時間をｘ秒とするとき、あとの（a)、(b)の問いに答えなさい。

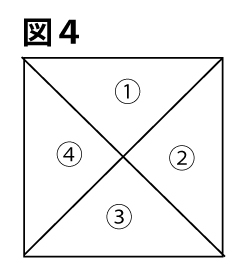
規則
は、1秒間色がついた後、1秒間色が消えることを繰り返す。
は、１秒間色がついた後、2秒間色が消えることを繰り返す。
は、2秒間色がついた後、1秒間色が消えることを繰り返す。
は、2秒間色がついた後、2秒間色が消えることを繰り返す。

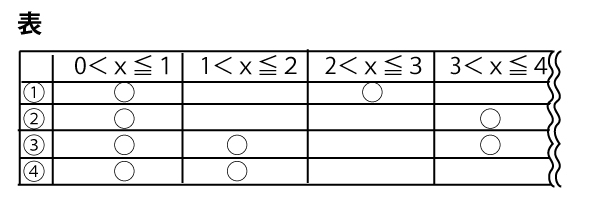
例えば、下の表は、０＜ｘ≦４のとき、色がつく部分を〇で示したものである。

（a)０＜ｘ≦１の時、は全て色がつく。その次にの部分に全て色がつくには、ア＜ｘ≦イの時である。ア、イに入る数をそれぞれ求めなさい。（完答で4点）（正答率25.7%（無答率24.8%))
（2）100＜ｘ≦101の時、色のつく部分はどれか。色がつく部分をのうちから選び、その番号をすべて書きなさい。
（順不同の完答で4点）（正答率13.9%（無答率27.9%))

[next_p]