2013年前期、千葉県公立高校入試「数学」第4問（総合問題、配点16点）問題・解答・解説

【解答】（計16点）
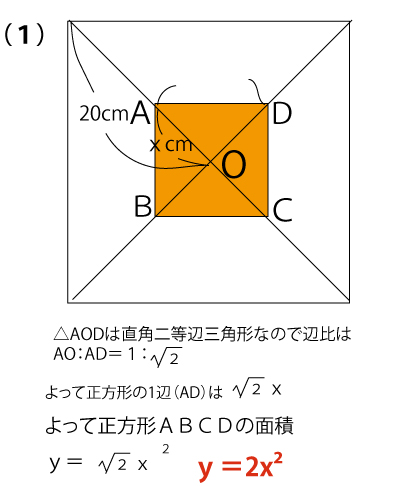
（1）ｙ＝2x²（4点）（正答率24.7%（無答率26.0%))

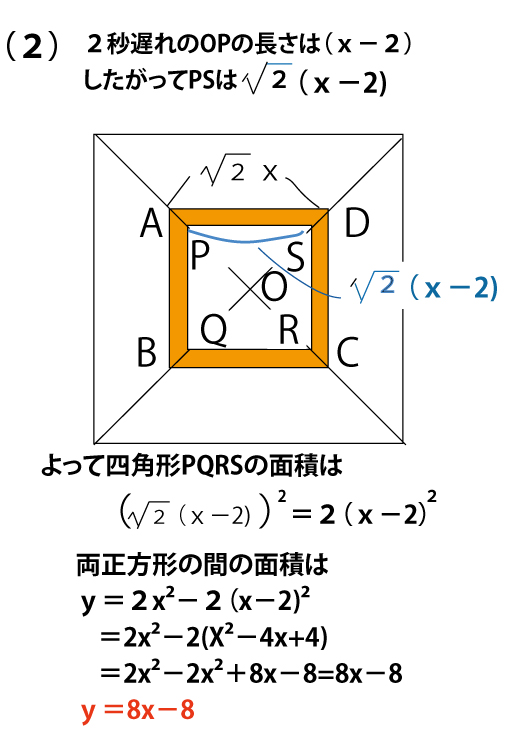
（2）ｙ＝8x－8（4点）(正答率6.9%(無答率51.3％））

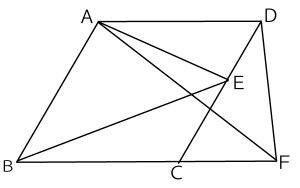
（３）(a)ア12、イ13　（完答で4点）（正答率25.7%（無答率24.8%))
（b)（順不同の完答で4点）（正答率13.9%（無答率27.9%))

【解説】

（3）０＜ｘ≦１、１＜ｘ≦２と範囲を書くのが正確であるが、簡略化のため、最大数だけで表を表してみる。a－１＜ｘ≦aの時を単にaと書いてみる（

０＜ｘ≦１は「１」、１＜ｘ≦２は「２」となる）。

の操作は4回ごとの繰り返し操作、 の操作は3回ごとの繰り返し操作なので、これらの操作の重なり状態は４と３の最小公倍数である12回ごとであることがわかる。
次に、繰り返しの単位を｜で示し、繰り返しの12回と少し2巡目に入った16回目までを表にしてみる。色がつかないことを×で示す。

（a)すると、ずべてに色がつくのは表の13、つまり、12（ア）＜ｘ≦13（イ）。

（b）100＜ｘ≦101は、上記の表記では101となる。
101＝12×８＋５
つまり、12回繰り返しを8回行った上で、次の回の5番目、つまり表の５と同じ色の付き方とわかる。
つまり表の５のように、