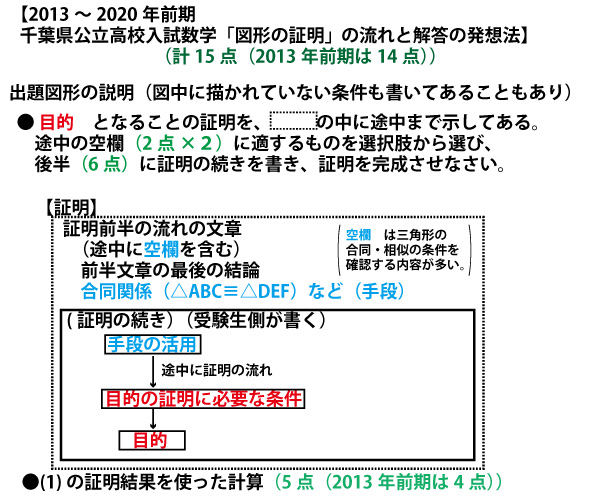
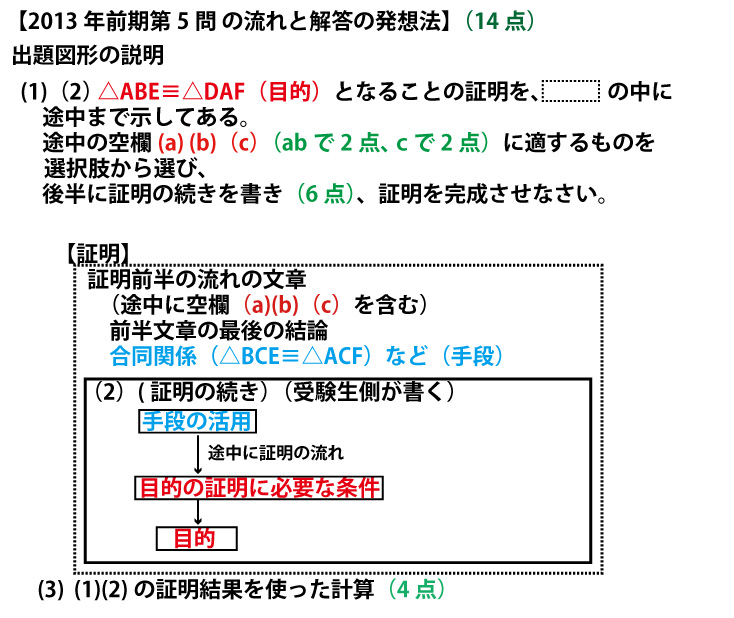
2013年前期、千葉県公立高校入試「数学」第5問（図形の証明、配点14点）問題・解答・解説
asakura
【解説】（2021年7月22日記述）
千葉県公立高校入試の「図形の証明」では、2013～2020年の8年間、以下のような、「手段→目的」の「2段階証明」の形で出題された。特に問題文の最初に証明すべきこと＝「目的」が明記してあること。前半の出題者自身が記述している部分の最後が「手段」となり、後半の「目的」の証明の流れの冒頭になることを理解しておくとよい。また「目的」の証明のためには、直接の条件として何が必要かを考えると、記述の部分の最後の目標がはっきりする。
なお、2021年は出題が変わり、「手段」→「目的」の「2段階証明」ではなく、1段階だけの証明の問題となった。おそらく2022年以降は、2021年型の1段階だけの証明の出題となると思われるが、念のため、2013～2020年の8年間、以下のような、「手段→目的」の「2段階証明」にも慣れておこう。
2013年前期のこの問題では以下のように考えられる。
★証明前半の理解と空欄（a)（b)（c）の答
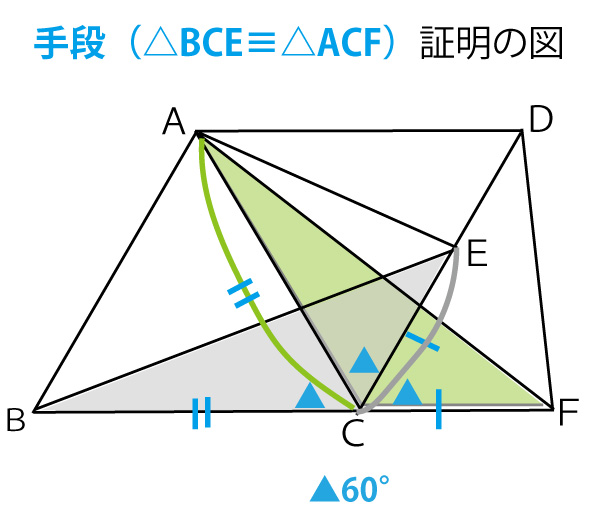
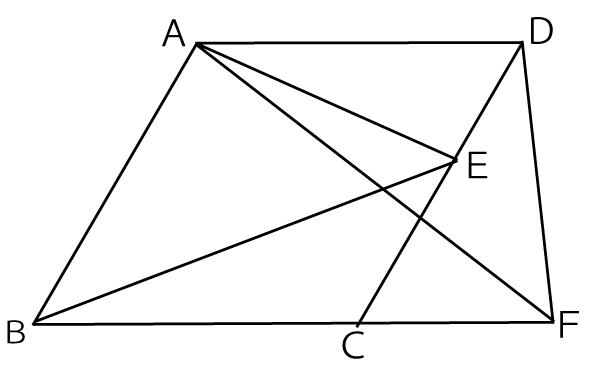
まず、問題文に書いてある証明の前半の流れを理解しながら、空欄（a)(b)を考えよう。証明冒頭に「△ABDと△CEDにおいて」と示されているし、前半の最後（後半のために使う「手段」の関係）に「△ABD≡△CED」と書いてあるので、この２つの三角形に注目しよう（以下画像では灰色に塗っているが、実際の入試では鉛筆書きの斜線で示すとよい）。
図の青線・青●に注目すると、空欄（a)（ｂ)（ｃ）は次のようになる。
2点ＡＣを結ぶ。
仮定から、四角形ＡＢＣＤの４つの辺は等しく、
∠ABC＝∠ADC＝60°なので
△ＡＢＣと△ＡＣＤは正三角形である。…
△BCEと△ACFにおいて、
仮定からＣＥ＝ＣＦ・・・
より、ＢＣ＝（a）AC（ア）・・・
また、∠BCA＝∠ACD＝60°なので
∠DCF=180°ー∠BCA－∠ACD=60 °となり
∠BCE＝（b）∠ＡＣＦ（オ）＝120°・・・
より （ｃ）イ（2辺とその間の角がそれぞれ等しい） ので
△BCE≡△ACF・・・・
（続く）
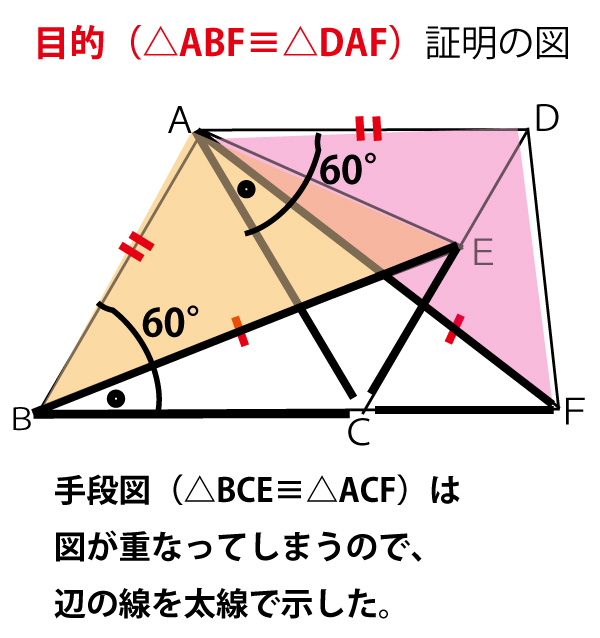
さて次の後半の図形の証明の記述（2）の流れを考えると以下のようになる。
△ABEと△DAFにおいて、
（△BCE≡△ACF）よりBE＝AF（図の｜）・・・
（△ＡＢＣと△ＡＣＤは正三角形である）より、△ABCと△ACDは1辺ACを共有する正三角形
であり、全ての辺の長さは等しいので
AB＝DA（図の｜｜）・・・
より∠CBE＝∠CAF（図の●）・・・
より、∠ABC＝∠CAD＝60°…
よって、
∠ABE＝∠ABCー∠CBE ＝60°ー∠CBE…
∠DAF＝∠CADー∠CAF＝60°－∠CAF…
より
∠ABE＝∠DAF…
より
２組の辺とその間の角がそれぞれ等しいので
△ABE≡△DAF
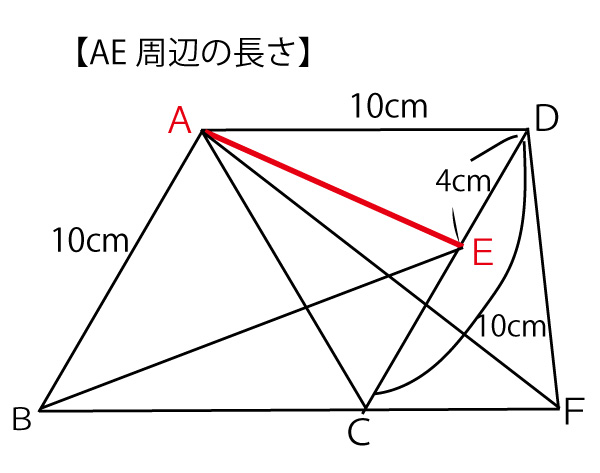
（3）与えられた条件から求めるべきAEの周辺の長さを求めている。
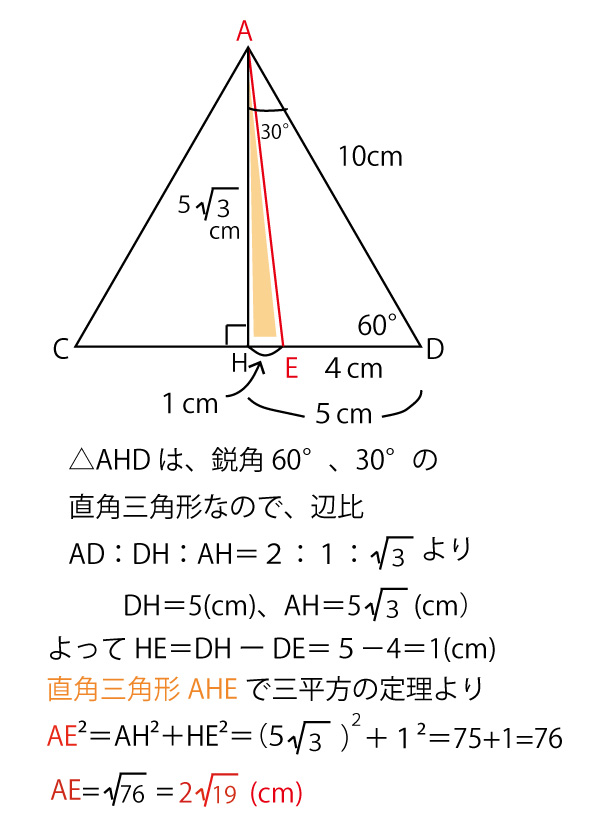
△ABCと△ACDは合同な正三角形なのでAB＝AD＝CD＝10cm
CE：ED＝3：2なので ED＝4cm。
次に正三角形ACDに注目して取り出し、CDを底辺にして表記し、AからCDへの垂線をひきその交点をHとしてみる。
【知っておきたい関連知識】
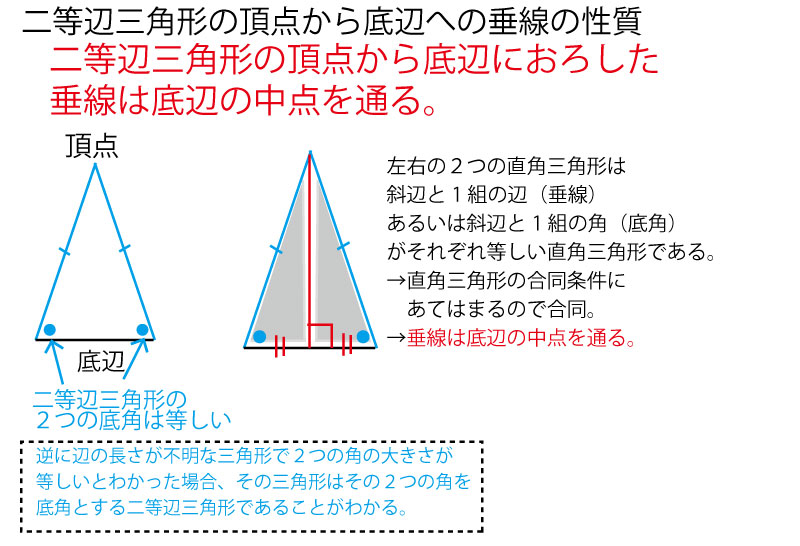
正三角形・二等辺三角形の2等辺の頂点から、対辺に下ろした垂線が対辺を二等分すること（この図ではDH＝5㎝）になることは、知っておいたほうがよい。
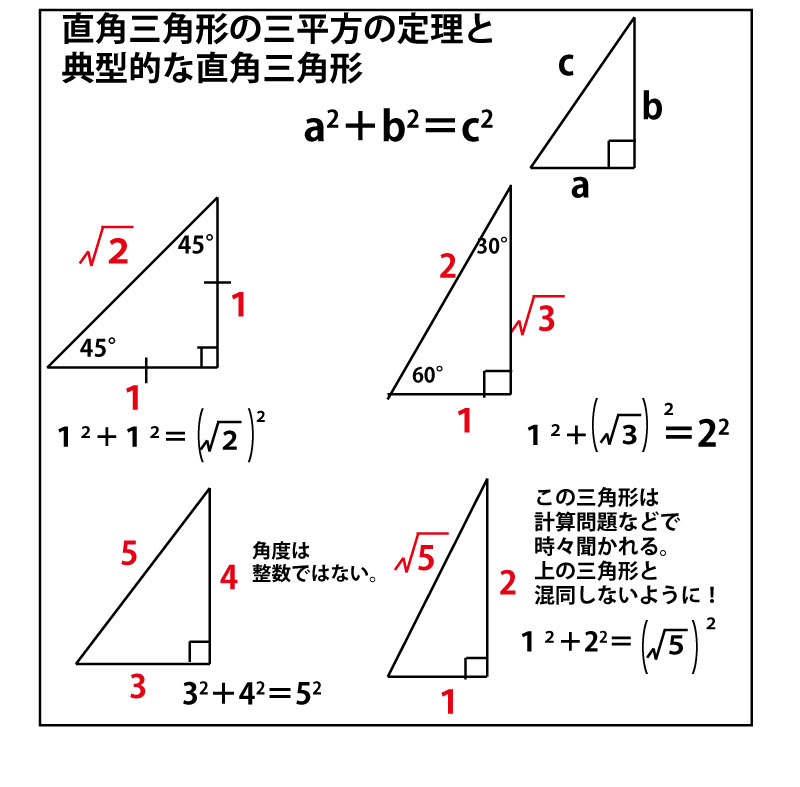
また、長さの計算の際には典型的な直角三角形の辺の比が聞かれることが多いので整理しておこう。
★参考 拙著「図形の証明」（他３著作）、アマゾンでお求めいただけます。
