2020年前期、千葉県公立高校入試「数学」第2問（5）（作図）問題・解答・解説（動画と文字での説明両方あり）

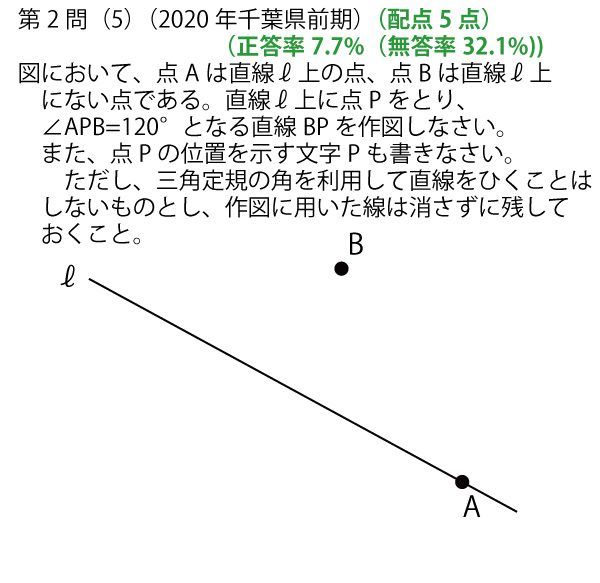
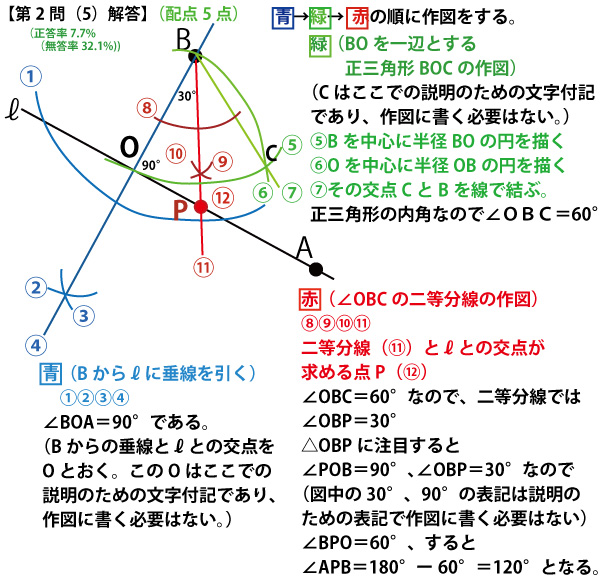
実際の作図そのものは、コンバスで描いた弧と点を結んで伸ばした線のみが残る。しかしそれではわかりにくいので、図には作図した順番と考え方を付記した。実際の図内に描いた番号や、説明のために書いた「点O」「点Ｃ」「90°」「30°」の表記は必要ない。また答えの強調のため、Ｐの位置に●を描いたが、実際の作図では必要なく、交点のわきにＰとだけ、書けばよいのでご注意ください。

2020年の出題でも、下記にまとめたように毎年基本とされている「垂直二等分線」「角の二等分線」「垂線」の作図が使われている。またそれに加えて、時々出題される「45°・60°・30°の作図」法、その中でも正三角形を作図から出発する60°。30°作図も使われている。

作図の基礎知識

どの年の問題での出題されていることが多い３種類の作図
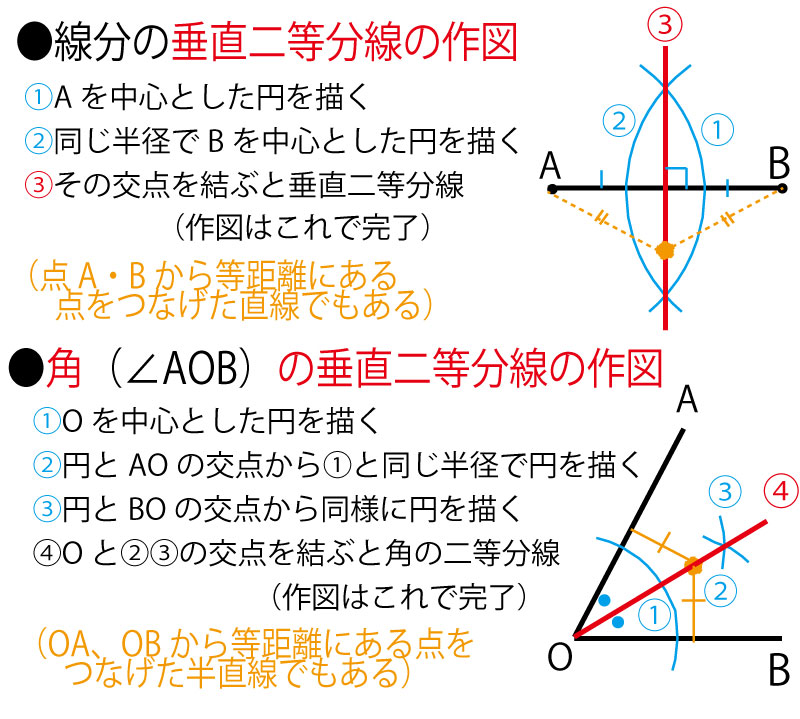
千葉県公立高校入試、第2問（5）の作図の問題では、作図に関わる様々な手法や知識が問われるが、一番使われる作図法は「垂直二等分線」と「角の二等分線」の作図である。どの年の問題でもこの２つのうちどちらかがを使う作図が出題されていると考えてほぼ間違いない。作図法を確認しておこう。

なお上記で垂直二等分線の作図①②、角の二等分線の作図①で弧を続けずに、コンパスをいったん紙から離し各直線のそばだけ作図する（弧を分離して作図する）方法でもよい。

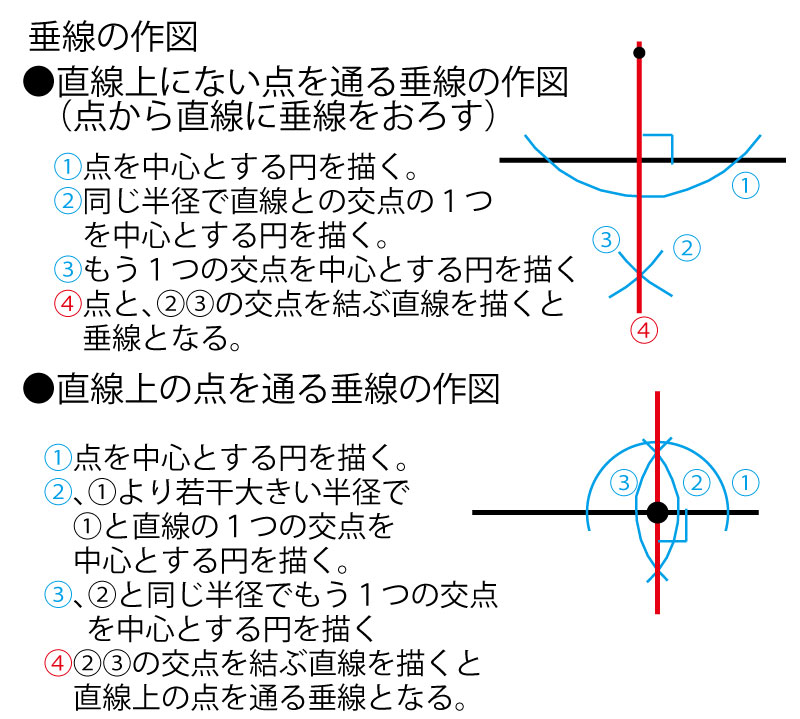
★次によくつかわれるのは垂線に関する作図である。作図法を確認しておこう。

なお上記「直線上にない点を通る垂線の作図」①、「直線上の点を通る作図」①②③で弧を続けずに、コンパスをいったん紙から離し各直線のそばだけ作図する（弧を分離して作図する）方法でもよい。

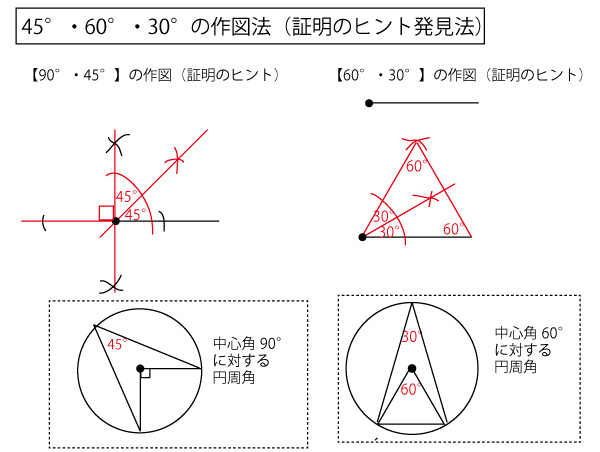
★垂線の作図と正三角形の作図ののち角の二等分線を使うと、45°・60°・30°の作図ができる。
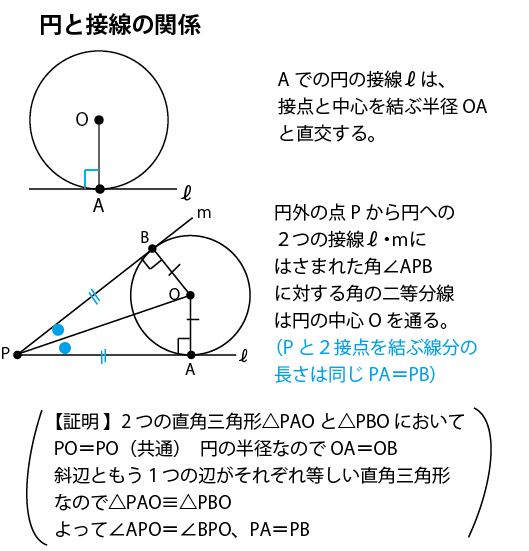
これは図形の証明の問題を解くヒントになることがあります。また中心角と円周角の関係を使うと、90°・60°中心角から、45°・30°円周角を描けます。

★円と接線との関係
作図の方針を考えていくためには、小中学校で学んだ三角形・四角形・円・角度などに関する様々な性質を知っておく必要がある。円と接線の関係を確認しておこう。