2020年前期、千葉県公立高校入試前期「数学」第2問(1)（y=ax2の変域）問題・解答・解説（動画解説・文字解説両方あり）

【解説】

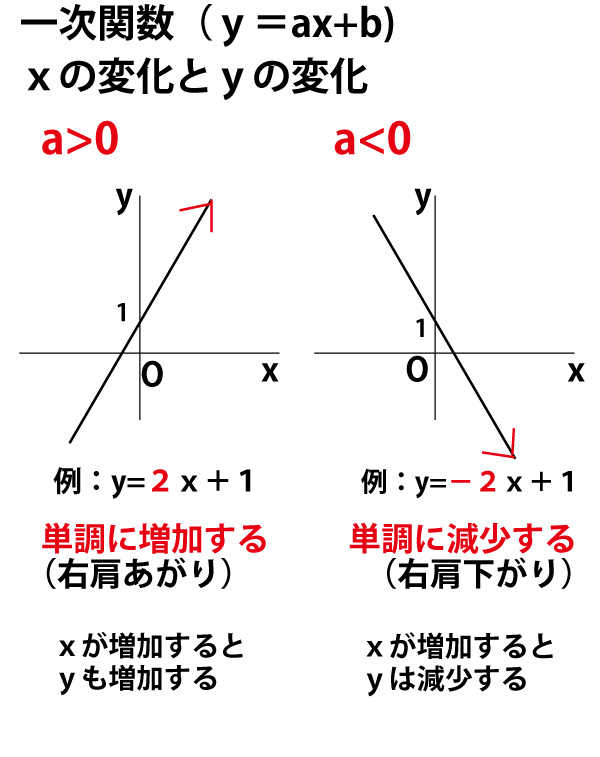
まず、一次関数のグラフとｘの増加に伴う、ｙの増加・減少を確認しよう。一次関数のグラフの直線は→（矢印）ではなく直線であるが、ｘが増加する方向の動きに→をあえてつけてわかりやすいようにしたのが以下の図である。

グラフは、ｘが増加するとｙが単調に増加する（a>0の場合）、ｘが増加するとｙが単調に減少する（a<0)の単純な動きとなる。
数学の世界での一次関数の座標上のグラフと似た図が経済・統計などで使われる。横軸に時間（年）の経過をとり、縦軸に経済指標・人口などを書くグラフを見たことがあると思う。この場合、よく「右肩上がり」「右肩下がり」という表現がよく使われる。ＺＯＯＭ会議などネット会議の利用者数は「右肩あがり」、一方年賀状の数は「右肩下がり」などと表現される。この表現は数学ではあまり使わないが、生活上で使う表現と連動させて考えるとイメージが広がる。
（この表現をあえて使うとa>0は単調に増加で「右肩上がり」であり、a<0は単調に減少で、「右肩下がり」である。）

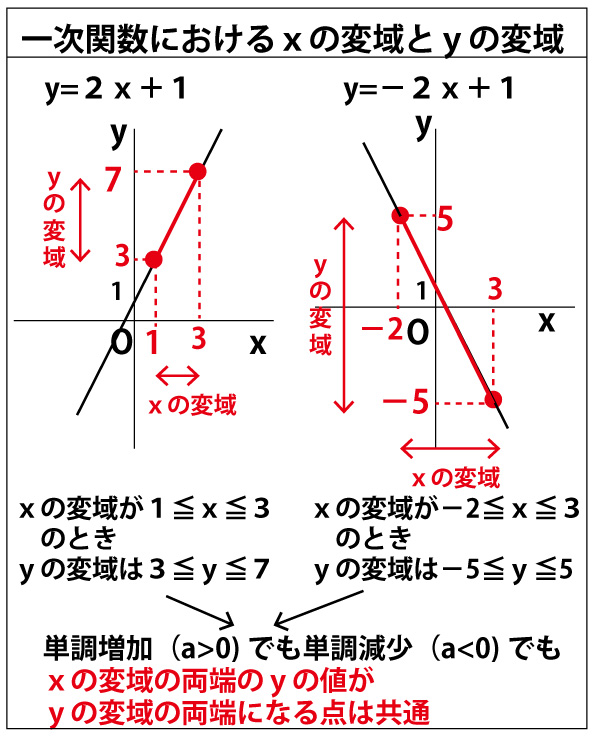
一次関数におけるｘの変域に伴うｙの変域はa>0の場合でもa<0の場合でも、以下のまとめのように「ｘの変域の両端のｙの値が、ｙの変域の両端となる」のでわかりやすい。

ところが、二次関数ｙ＝ax²では「ｘの変域の両端のｙの値が、ｙの変域の両端となる」とは限らない。「ｘの変域の両端のｙの値が、ｙの変域の両端となる」という思い込みで答える人が多いので、正答率は57.7％（つまり42.3%が誤答か無答）と低い。

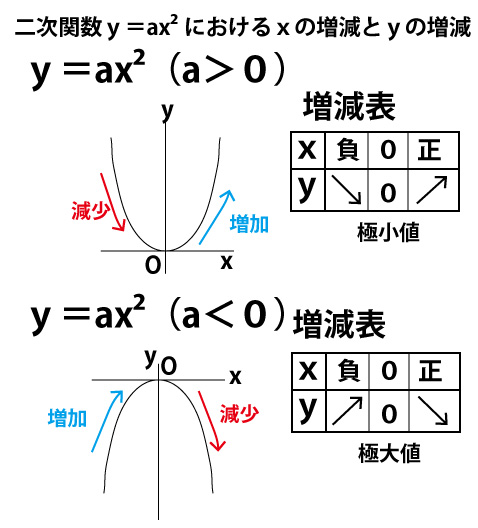
二次関数ｙ＝ax²のグラフとの形と増減の様子を確認しよう。ｘの値を増加させていくと、負→０→正の「０」のところで、減少→増加、増加→減少に転じる。この点を高校数学では「変曲点」と学ぶ。「曲がり方が変わる点」である。a>0の場合はｙの値は０を最小に増加に展じ、０より小さい値（負の値）をとることはない。ｙがとり得る最小値０を高校数学では「極小値」という。
a<0の場合はｙの値が０を最大に減少に展じ、０より大きい値（正の値）をとることはない。ｙがとり得る最大値０を高校数学では「極大値」と呼ぶ。
「増減表」も高校数学で学ぶものだが、ｘの増減に伴うｙの増減を→の向きで表すものでわかりやすいので、中学でも知っておいたほうがよいでしょう。（知らなくても入試に困ることはないです。また高校に行くと更にこの増減表を深く学びます）

ｘの変域が正負にまたがらない場合（負≦ｘ≦負（０）、正（0）≦ｘ≦正）は、下図のように一次関数と同様、「ｘの変域の両端のｙの値が、ｙの変域の両端となる」。

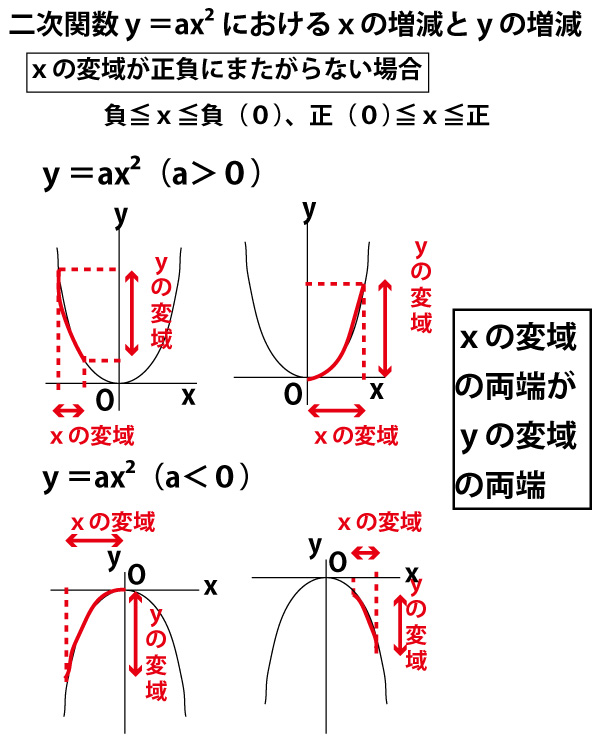
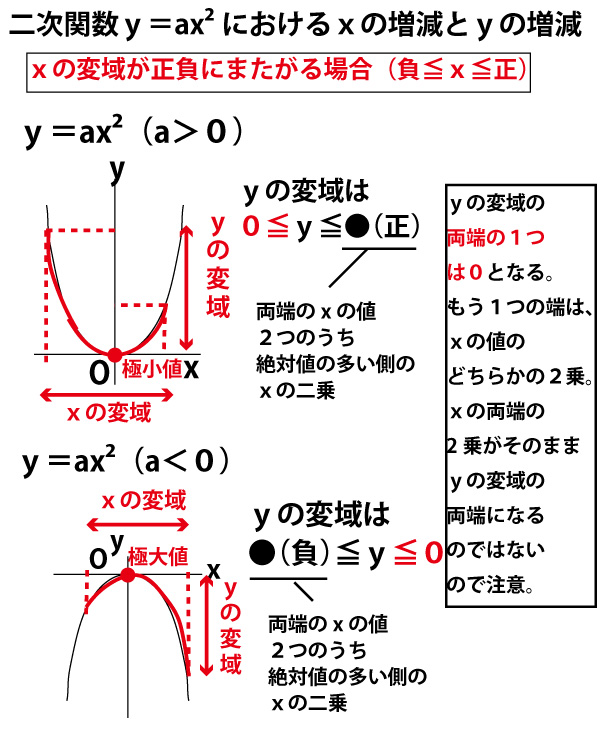
しかし、ｘの変域が正負にまたがる場合、範囲に「変曲点」となり、極大値・極小値となる原点（ｘもｙも０）を含み、そこで増減がかわる影響でｙの変域の範囲は以下の図のようになります。

図で示したように、ｙの変域の両端は単純にｘの変域の両端の２乗となるのではありません。ｙの変域の端の１つは０となり、もう１つはｘの両端のうち、絶対値が大きいほうの値の2乗になります。

本設問では、ｙの変域が－９≦ｙ≦０なので、ｘの変域は正負にまたがるものです。するとエ（－１≦ｘ≦３）が正解で、絶対値が大きい側のxの端の値３で－３²＝－9なので、
－９≦ｙ≦０であることが確認できます。

ちなみにそれぞれの選択肢の場合のｙの変域は以下のようになります。

ア、－１≦ｘ≦０　ｙの変域　－１≦ｙ≦０
イ、－３≦ｘ≦－１　ｙの変域　－９≦ｙ≦－１
ウ、１≦ｘ≦３　　　ｙの変域　－９≦ｙ≦－１
エ－１≦ｘ≦３　　ｙの変域　　－９≦ｙ≦０