2020年前期、千葉県公立高校入試「数学」第2問（4）（確率）（配点5点）問題・解答・解説（動画と文字両方あり）

【解説】

まずは、有理数と無理数の定義を確認しよう。

以下、発展学習で、ここまで高校入試に出題される可能性は低い（ないわけではない）が面白い考え方なので、循環小数が分数に転換できる方法を見ておこう。

「無理数」は「有理数ではない数」、つまり分数で示すことができない数と定義される。

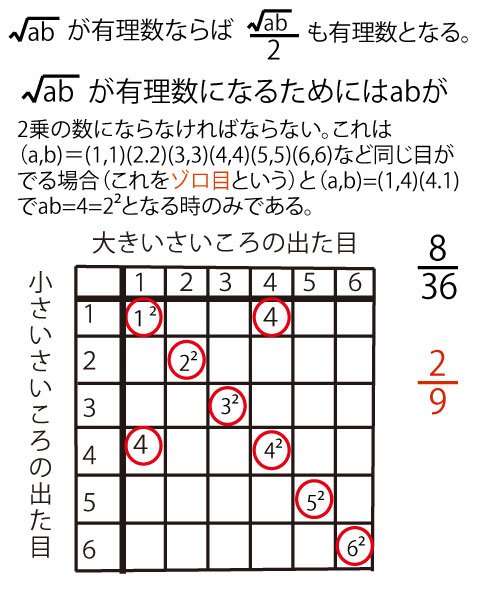
次に、この設問の本題に入る。大きいさいころの出る目は１～６の６通り、ちいさいさいころの出る目は１～６の6通りであるので、同時に振ってでる目の場合の数は
６×６＝36通りがある。その36通りの中で、どれが、設問の条件にあうのかを碁盤目に書き、その数を数えて、36を分母、条件に合う出方を分子として求めた分数が確率となる。