2021年大学入試共通テスト「数学IA」第3問(確率、配点20点、選択)問題・解答・解説
2021年4月 予備校講師、「円」「三角形」「図形の証明」著者、船橋市議 朝倉幹晴
2021年1月17日(日)に実施された大学入試共通テスト数学IA第3問(ア~ト)(計20点、選択、第3~5問(いずれも20点)から2問選択)の問題・解答・解説です。
2022年以降の受験生は来年の準備にご活用ください。
実際の入試問題は白黒印刷ですが、画面上ですのでカラーを一部使いました。ア~トには当てはまる数字か選択肢の番号を入れる形で答えてください。
第3問(20点配点、選択)
中にくじが入っている箱が複数あり、各箱の外見は同じであるが、当たりくじを引く確率は異なっている。くじ引きの結果から、どの箱からくじを引いた可能性が高いかを、条件付き確率を用いて考えよう。
(1)当たりくじを引く確率が![]() である箱Aと、当たりくじを引く確率が
である箱Aと、当たりくじを引く確率が![]() である箱Bの二つの箱の場合を考える。
である箱Bの二つの箱の場合を考える。
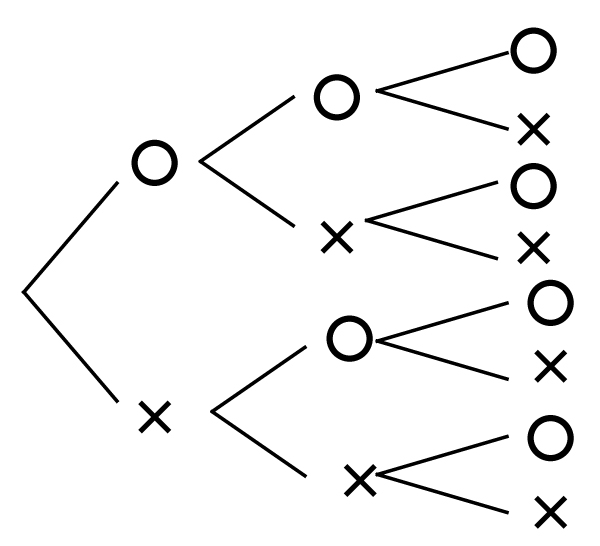
(i)各箱で、くじを1本引いてはもとに戻す試行を3回繰り返したとき
箱Aにおいて、3回中ちょうど1回当たる確率は![]() (2点)・・・
(2点)・・・![]()
箱Bにおいて、3回中ちょうど1回当たる確率は![]() (3点)・・・
(3点)・・・![]()
である。
(ⅱ)まず、AとBのどちらか一方の箱をでたらめに選ぶ。次にその選んだ箱において、くじを1本引いてはもとに戻す試行を3回繰り返したところ、3回中ちょうど1回当たった。このとき、箱Aが選ばれる事象をA、箱Bが選ばれる事象をB、3回中ちょうど1回当たる事象をWとすると
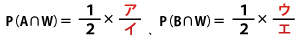
である。![]() であるから、3回中ちょうど1回当たったとき、選んだ箱がAである条件付き確率Pw(A)は
であるから、3回中ちょうど1回当たったとき、選んだ箱がAである条件付き確率Pw(A)は![]() (3点)となる。また、条件付き確率Pw(B)は
(3点)となる。また、条件付き確率Pw(B)は (2点)となる。
(2点)となる。
(2)(i)のPw(A)とPw(B)について、次の事実(*)が成り立つ。
事実(*)
Pw(A)とPw(B)のスは、![]() の確率と
の確率と![]() の確率のス に等しい。
の確率のス に等しい。
(3)花子さんと太郎さんは事実(*)について話している。
花子:事実(*)はなぜ成り立つのかな?
太郎:Pw(A)とPw(B)を求めるのに必要なと
の計算で、
、
の確率に同じ数
をかけているからだよ。
花子:なるほどね。外見が同じ三つの箱の場合は、同じ数をかけることになるので、同様のことが成り立ちそうだね。
当たりくじをひく確率が、![]() である箱A、
である箱A、![]() である箱B、
である箱B、![]() である箱Cの三つの箱の場合を考える。まず、A、B、Cのうちどれか一つの箱をでたらめに選ぶ。次にその選んだ箱において、くじを1本引いてはもとに戻す試行を3回繰り返したところ、3回中ちょうど1回当たった。このとき箱がAである条件付き確率は
である箱Cの三つの箱の場合を考える。まず、A、B、Cのうちどれか一つの箱をでたらめに選ぶ。次にその選んだ箱において、くじを1本引いてはもとに戻す試行を3回繰り返したところ、3回中ちょうど1回当たった。このとき箱がAである条件付き確率は となる。
となる。
(4)
花子:どうやら箱が三つの場合でも、条件付き確率のスは各箱で3回中ちょうど1回あたりくじを引く確率のスになっているみたいだね。
太郎:そうだね。それを利用すると、条件付き確率の値は計算しなくても、その大きさを比較することができるね。
当たりくじをひく確率が、![]() である箱A、
である箱A、![]() である箱B、
である箱B、![]() である箱C、
である箱C、![]() である箱Dの四つの箱の場合を考える。まず、A、B、C、Dのうちどれか一つの箱をでたらめに選ぶ。次にその選んだ箱において、くじを1本引いてはもとに戻す試行を3回繰り返したところ、3回中ちょうど1回当たった。このとき、条件付き確率を用いて、どの箱からくじを引いた可能性が高いかを考える。可能性が高い方から順に並べるとトとなる。
である箱Dの四つの箱の場合を考える。まず、A、B、C、Dのうちどれか一つの箱をでたらめに選ぶ。次にその選んだ箱において、くじを1本引いてはもとに戻す試行を3回繰り返したところ、3回中ちょうど1回当たった。このとき、条件付き確率を用いて、どの箱からくじを引いた可能性が高いかを考える。可能性が高い方から順に並べるとトとなる。
[next_p]