2021年千葉県公立高校入試「数学」第2問（1）（資料の整理・統計）（配点5点）問題・解答・解説
asakura
解答 ウ（生徒20人が借りた本の冊数の中央値（メジアン）は2冊である。）
解説
ア「生徒20人が借りた本の冊数の合計は40冊である。」 ×
借りた本の総冊数は
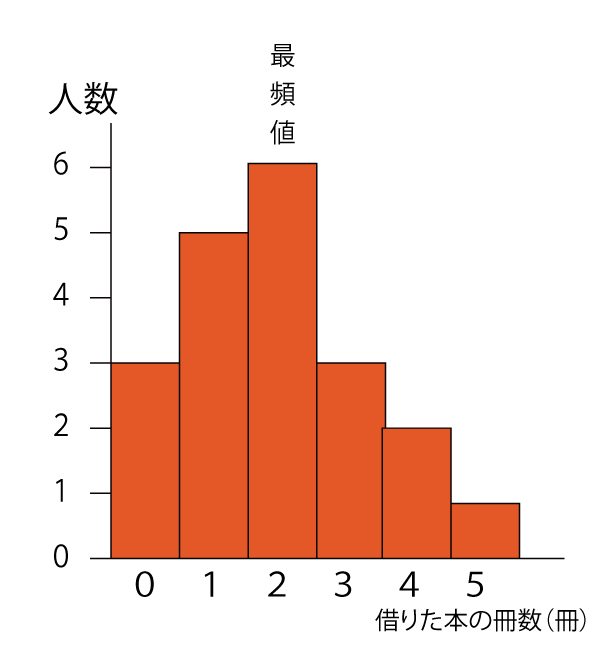
０冊×3（人）＋1冊×5（人）＋2冊×6（人）＋3冊×3（人）＋4冊×2（人）＋5冊×1（人）＝０＋５＋12＋９＋８＋５（冊）＝39冊
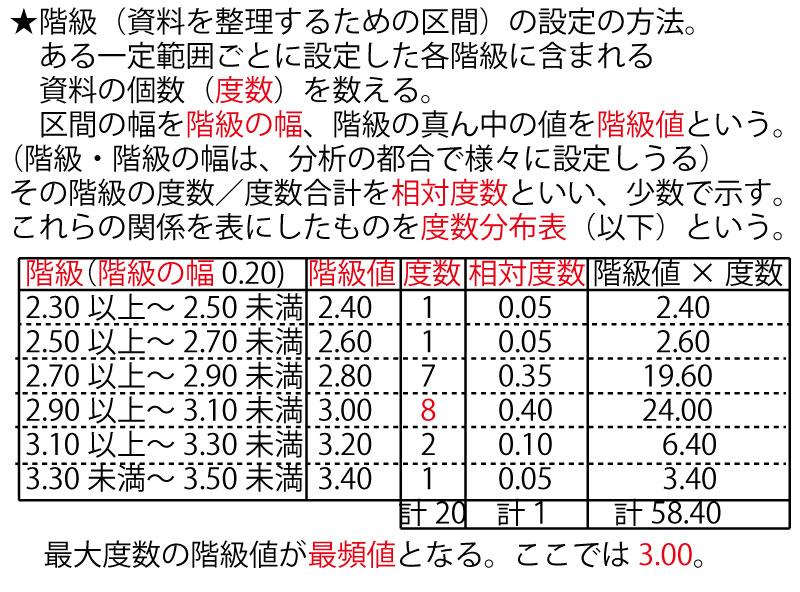
イ「生徒20人が借りた本の冊数の最頻値（さいひんち・モード）は1冊である。」×
最頻値は2冊である。ヒストグラムで示すと以下のようになる。
ウ 「生徒20人が借りた本の冊数の中央値（メジアン）は2冊である。」〇
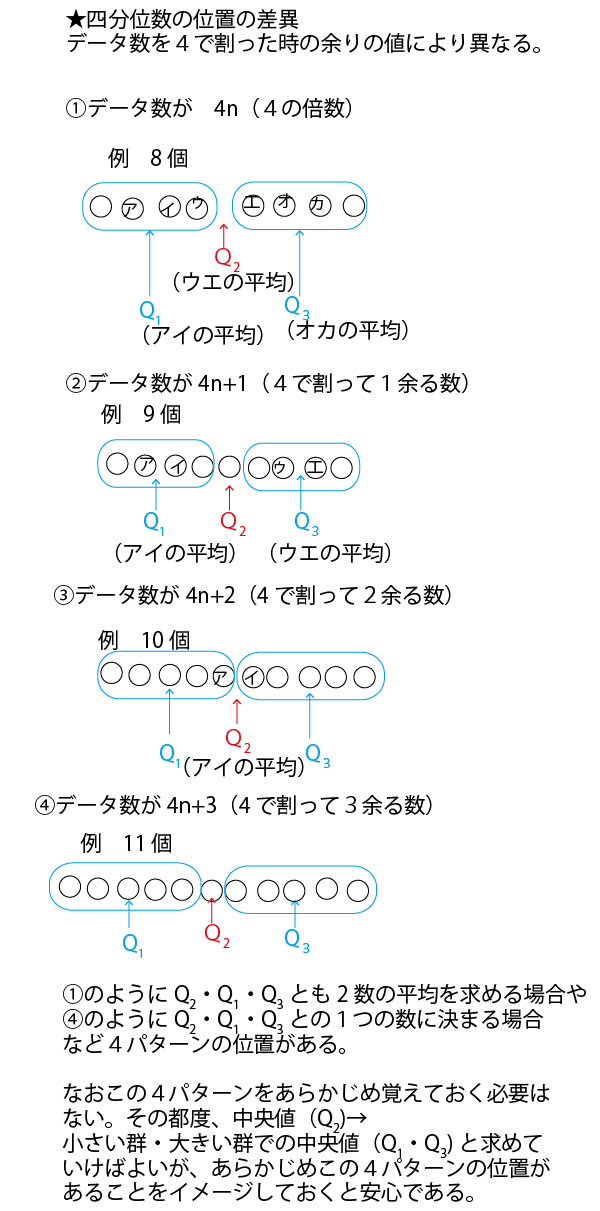
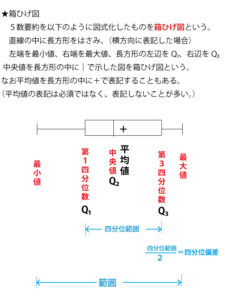
中央値とは、資料の値を大きさの順（大きい順、あるいは小さい順）に並べた時の中央の値。資料が奇数個の場合は中央が決まるが、偶数個の場合は、中央の２つの値の平均値である。
本設問では、20人なので、小さい順から10人目と11人目の値の平均値となる。
列記すると ０冊、０冊、０冊、１冊、1冊、1冊、1冊、1冊、2冊、2冊（10人目）
2冊（11人目）、2冊、2冊、2冊、3冊、3冊、3冊、4冊、4冊、5冊
したがって 2冊と2冊の平均なので中央値は2冊。
列記するのはたいへんなので、以下のように足し合わせて累計値を求め、10、11番目がどこにあるかを確認すればよい。
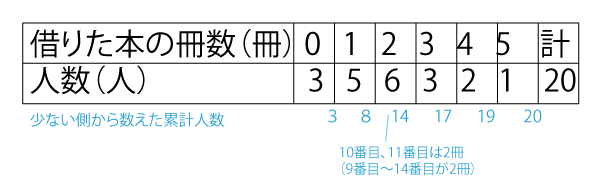
エ 「生徒20人が借りた本の冊数の平均値より多くの本を借りた生徒は6人である。」×
平均値は「借りられた本の合計冊数÷人数」で、39冊÷20人＝1.95冊。
平均値（1.95冊）より多い冊数は2冊、3冊、4冊、5冊なので
6人＋3人＋２人＋1人＝12人。
★「資料の整理」（統計）の過去7年の問題
2020年前期、第2問（2）（資料の整理）（5点）
2019年前期第2問（1）（資料の整理）（5点）
2018年前期、第2問（2）（資料の整理）（5点）
2017年前期、第2問（2）（資料の整理）（5点）
2016年前期、第２問（２）（資料の整理）（５点）
2015年前期、第2問（1）（資料の整理）（5点）
2014年前期、第2問（3）（標本調査の活用）（5点）
★【中学「資料の整理」）】分野のまとめ
