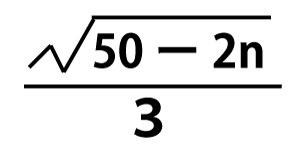2012年前期、千葉県公立高校入試「数学」第2問(3)(立体図形の体積・表面積、配点5点)問題・解答・解説

【解答】
(正答率17.2%(無答率11.8%))
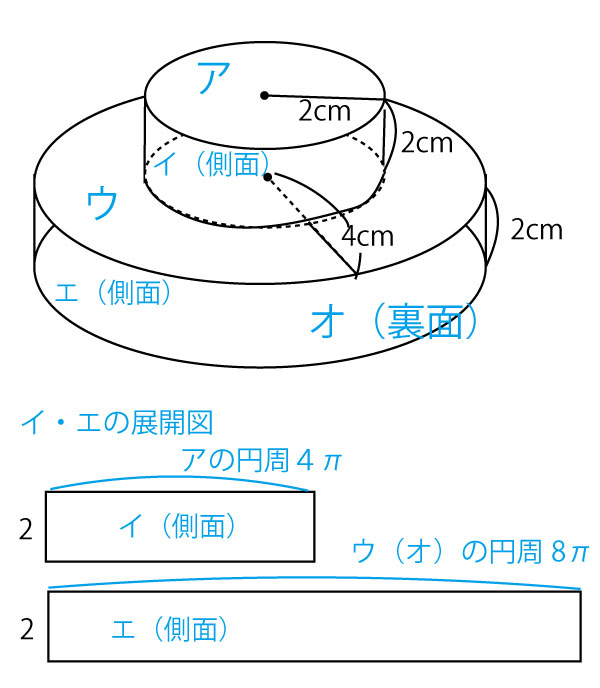
【解説】表面積は以下の図のア~オを足し合わせたものになる。
ア・ウを真上から見たと考えると、アとウを足すとちょうど、オ(裏面)と同じ面積になるがわかる。
オは半径4の円なので、面積は![]() ×42=16
×42=16![]() 。
。
次に側面積イとエを考える。
イは展開図を描くと縦2、横4![]() (上の円(半径2の円)の円周)。
(上の円(半径2の円)の円周)。
エは展開図を描くと縦2、横8![]() (下の円(半径4の円)の円周)。
(下の円(半径4の円)の円周)。
イ+エ=2×4![]() +2×8
+2×8![]() =8
=8![]() +16
+16![]() =24
=24![]()
よって
ア+イ+ウ+エ+オ=32![]() +24
+24![]() =
=![]()
体積(cm3)ではなく、表面積(cm2)であることに注意。
もし体積を求める問題であった場合は、
上の円柱の体積=底面積(半径2の円)×高さ2=×22×2=8
実は、千葉県公立高校入試のこの第2問の小問で時折出題される「立体」の問題では、「体積」と「表面積」を勘違いすると回答を間違ってしまうので、注意すること。問題を見た瞬間に「体積」あるいは「表面積」の文字を〇で囲んで強調しておくとよい。
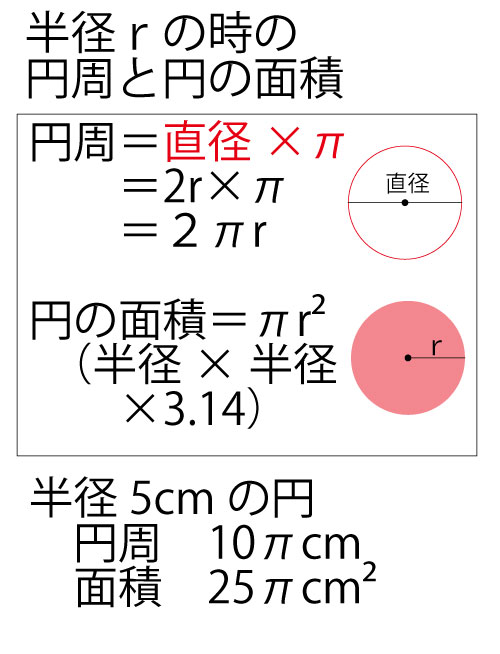
【円周と円の面積】
円周(長さ)と円の面積は、求める公式が2![]() r、
r、![]() r2と似通って見えるので混同し計算を間違いやすい。間違いやすい人は、円周は、小学校で学んだ定義のように、「直径×
r2と似通って見えるので混同し計算を間違いやすい。間違いやすい人は、円周は、小学校で学んだ定義のように、「直径×![]() 」であるとし、直径は頭の中で、半径を2倍して求めるようにしたほうがよいかもしれない。
」であるとし、直径は頭の中で、半径を2倍して求めるようにしたほうがよいかもしれない。