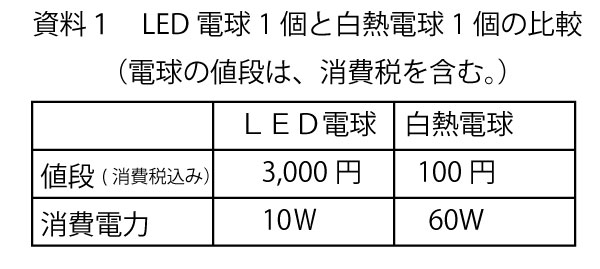
2012年前期、千葉県公立高校入試「数学」第3問（白熱電球・LED電球比較問題、配点計16点）問題・解答・解説

【解答】（計16点）

360（2点、正答率62.9%（無答率3.5%))　　40(2点、正答率48.1%（無答率21.5%))

20(2点、正答率49.7%（無答率22.5%))　　200(2点、正答率53.6%（無答率13.1%))

46(2点、正答率19.8%（無答率32.0%))　　276x＋100(2点、正答率13.2%（無答率44.5%))

276ｘ＋200(2点、正答率8.4%（無答率54.1%))　11(2点、正答率3.9%（無答率39.2%))

【解説】

　1000世帯への調査は「標本調査」であり、全世帯30000世帯でも同じ比率でエアコンを購入していると推定できるので、全市での購入世帯をx世帯とおくと、
1000：12＝30000：ｘ

　　　　1000ｘ＝12×（かける）30000＝360000
x=360

LED電球をｘ個、白熱電球をｙ個とおいて、購入金額と消費電力に関して連立方程式を作り、それを解く。

本文に「ある照明一箇所の１か月の使用時間を200時間」とあるので、寿命の時間数を200で割れば、寿命が何か月かがわかる。
LED電球は　40000÷200＝200か月（答）

白熱電球は　1000÷200＝5か月

LED電球での1か月の消費電気料金は　0.23円（1時間あたり）×200時間＝46円。
ｘか月後の総費用は　ｙ＝46ｘ（消費電気料金）（答）＋3000（購入費）

白熱電球での1か月の消費電気料金は　1.38円（1時間あたり）×200時間＝276円。
ｘか月後の消費電気料金は、276xである。
ただ、電球は5か月ごとに1個、100円で買うことになるので
０≦ｘ≦５は1本目で　ｙ＝276ｘ＋100（答）
５＜ｘ≦10では2本目を買ったことになるので、ｙ＝276x＋200（答）

購入額は高いが耐久性があり、消費電力が少ないLED電球が、何か月使用継続時点から、白熱電球よりも安くなるかを考えさせるという日常生活に密着した問題である。数学が生活や地球環境を考えるを考えるのに役立つことを感じてほしい。
与えらえた白熱電球の総費用のグラフに、LED電球のグラフ（一次方程式ｙ＝46x＋3000）を書き入れ、両者が交差し、白熱電球の額が上回るのが何か月であるかを求めればよい。式を書き込んでみると以下のようになる。

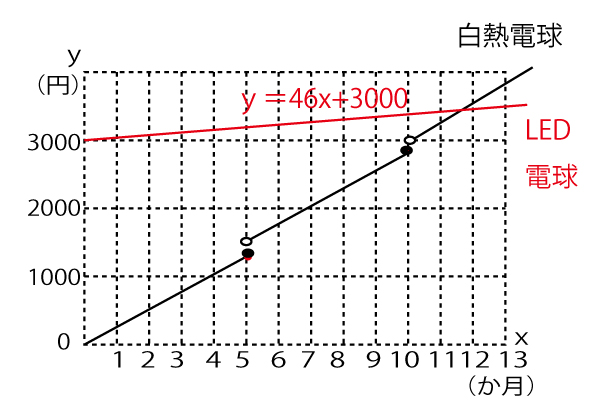
グラフからに10＜ｘ≦15に交点があることが推定できるので、白熱電球は3本目となり、
ｙ＝276ｘ＋300となる。
よって交点のｘの値は
276ｘ＋300＝46ｘ＋3000
276ｘー46ｘ＝3000ー300
230ｘ＝2700
23x＝270

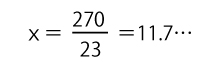
よって11か月までは（答）LED電球の総費用が（白熱電球の総費用より）高いが、12か月後以降から、白熱電球のほうが高くなる（LED電球のほうが安くなる）。