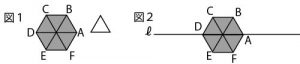【2017年前期・千葉県公立高校入試数学】第4問(図形の証明)問題・解答・解説
【はじめに】私は、様々な理由で受験や進学で不利になっている子どもたち(原発被災避難世帯、児童養護施設、母子生活支援施設、ひとり親家庭など)の学習サポートを続けてまいりました。しかし直接伺える場所・教えられる子どもの数は限られますので、どなたでもご覧いただけるように、公式サイトにその内容をUPすることにいたしました。どうぞご活用ください。
【注意事項】
①前半に問題、後半に解答解説があります。問題にじっくりとりくみ考えたい人は、「以下解答解説です」の画像のところで画面を止める(印刷した場合はそれより下を見ない)ようにしてください。
②入試問題は実際は、白黒です。ただせっかくの画像上ですので、カラーをつけました。
【千葉県公立高校入試】前期数学第4問(15点)
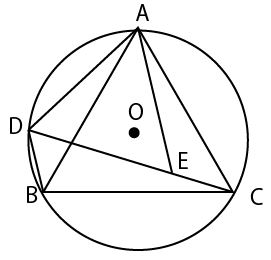
図のように、円Oの円周上にある3点A、B、Cを頂点とする正三角形ABCがある。点Cを含まないAB上に、2点A、Bとは異なる点Dをとり、点Dと、3点A、B、Cをそれぞれ結ぶ。線分CD上に、BD=CEとなる点Eをとり、点Aと点Eを結ぶ。このとき、次の(1)(2)の問いに答えなさい。
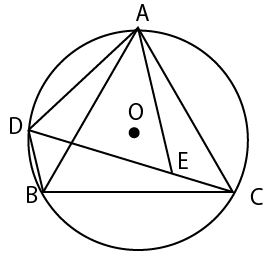
(1)△ADEが正三角形となることの証明を、下に途中まで示してある。(a) 、(b) に入る最も適当なものを、選択肢ア~カの
うちから1つずつ選び、符号で答えなさい。また(c)には証明の続きを書き、証明を完成させなさい。ただし、下の①~④に示されている関係を使う場合、番号の①~④を用いてもかまわないものとする。
【証明】
△ABDと△ACEにおいて
仮定から、BD=CE ・・・①
△ABCは正三角形なので、
AB=AC ・・・②
ADに対する円周角は等しいので、
∠ABD= (a) ・・・③
①、②、③より
(b) がそれぞれ等しいので、
△ABD≡△ACE ・・・④
(c)
【選択肢】 ア∠DEA イ∠EAC ウ∠ACE エ3辺 オ2辺とその間の角 カ1辺とその両端の角

(2)AD=2cm、BC=3cmのとき、線分CEの長さを求めなさい。


【解答】(1)(a)ウ(2点) (b)オ(2点) (c)(6点)(解説参照)
文章での解説を以下にします。文章とは別に、東大大学院特任研究員のアドバイスも受けながら、慈恵医大・共立女子大学生の協力で作成した動画もあります。あわせてご参考にください。
解説動画(8分、2017年前期第4問「図形の証明」)
(なお動画での説明は、動画の性質上、以下の文章での説明と微妙に異なる部分もあります。ただ大筋は共通です。)
【解説】
千葉県公立高校入試の第4問【証明】の問題の流れは以下のようになる。特に問題文の最初に証明すべきこと=「目的」が明記してあること。前半の出題者自身が記述している部分の最後が「手段」となり、後半の「目的」の証明の流れの冒頭になることを理解しておくとよい。また「目的」の証明のためには、直接の条件として何が必要かを考えると、記述の部分の最後の目標がはっきりする。
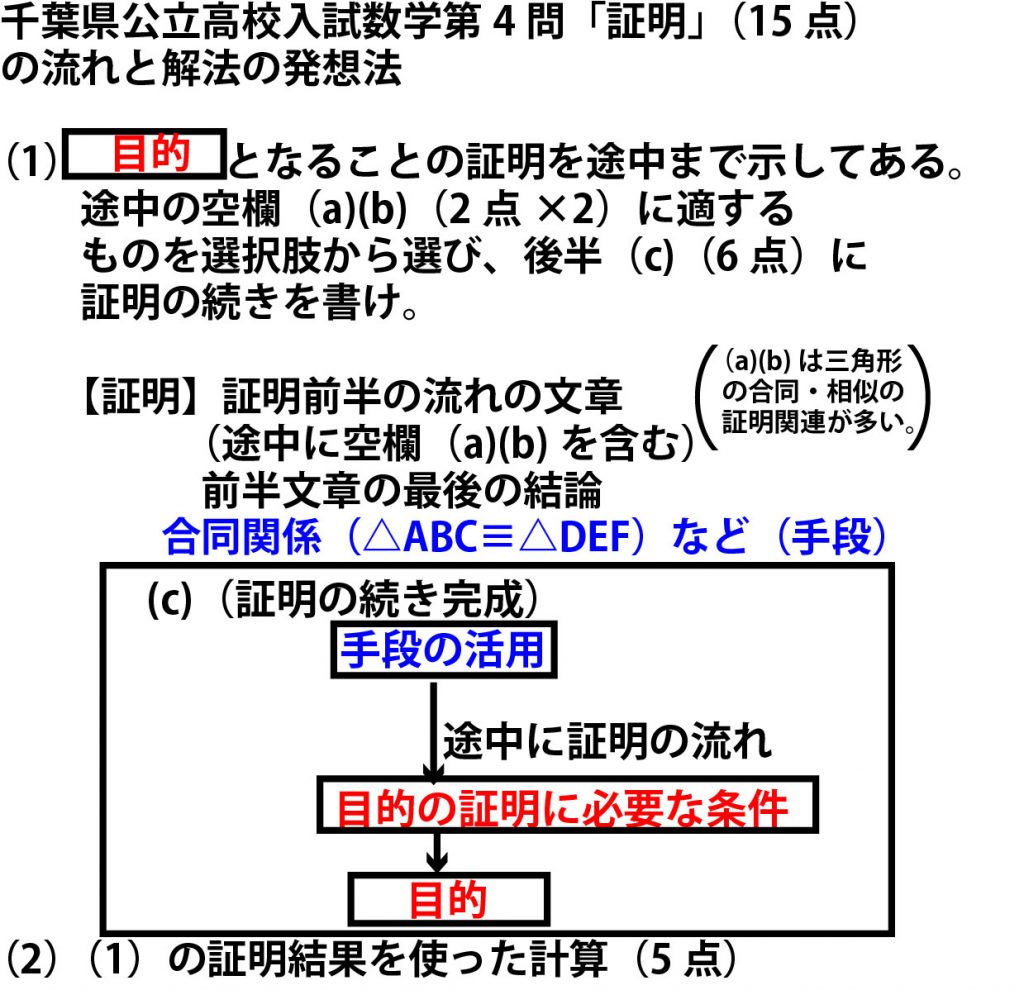
この流れの見方で、この設問の解法にいたる流れか考えるとと以下のようになる。これを意識しながら証明を進めていくようにするとよい。

★証明前半の理解と空欄(a)(b)の答
まず、問題文に書いてある証明の前半の流れを理解しながら、空欄(a)(b)を考えよう。その際、問題文にある3つの図のうち1番目の図を前半理解のための書き込みの図に使う。
証明冒頭に「△ABDと△ACEにおいて」と示されているし、前半の最後(後半のために使う「手段」の関係)に「△ABD≡△ACE」と書いてあるので、
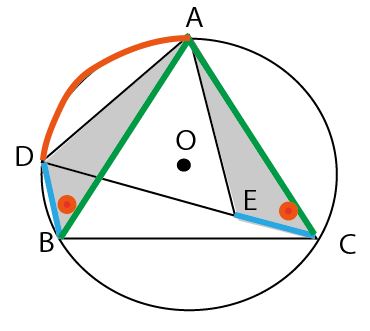
この2つの三角形に注目しよう。そして問題文のある3つの図のうち1番目の図にそれを書き入れよう。(以下画像では灰色に塗っているが、実際の入試では斜線で示す)
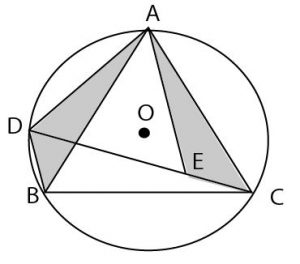
この2つの三角形の合同を証明するために、文章の順に基づき、以下の3色で示した部分を図に書き入れていく。(図では色で示したが実際の試験では太線や線の真ん中に線を入れることで示す)
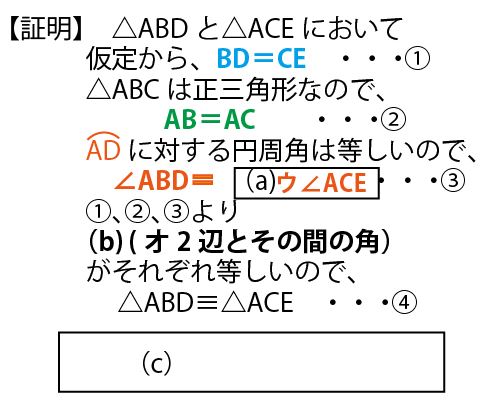
★後半の証明のための方針を立てる。
後半の証明のためまず方針を考えてみよう。正三角形を証明すべき三角形は以下の三角形である。
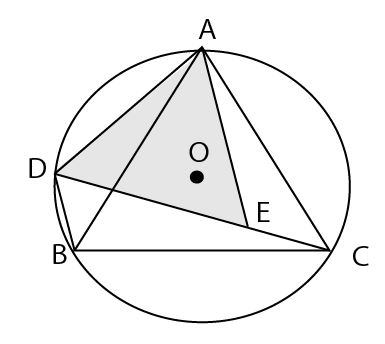
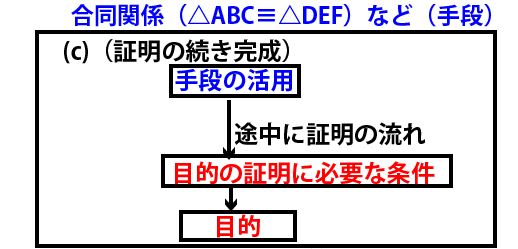
正三角形であることの証明のためには「3辺の長さが等しい」か「3角がそれぞれ60°で等しい」をしめせばよいが、DEがAD・AEと等しい長さであることを証明するのには材料が少ない。
一方、3角が60°であることは正三角形ABCの角が60°であることや、円周角を使えばできそうである。したがって「3角が60°である」ことを示す流れを考えてみる。
★前半と後半のつなぎ(後半の出だし)
前半の最後で証明した三角形の合同から、後半の証明に必要な辺や角の関係が類推できる。これからの関係は問題の2番目の図に書き込んでいく。
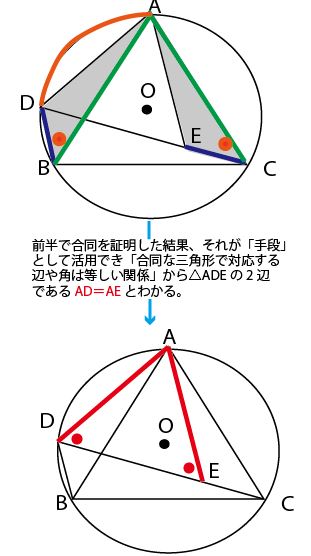
図のように△ADEはまずは二等辺三角形であることがわかり、「二等辺三角形の底角は等しい」関係から図の赤●が同じ角度と証明できる。
更に、図のオレンジの角と赤丸∠ADEは弧ACに対する円周角で等しく、またオレンジの角は正三角形ABCの角なので60°とわかるので、
オレンジも赤丸もすべて60°とわかる。すると残りの∠DAEも60°とわかるので、△ADEはすべての内角が60°で正三角形と証明できる。
【文章化】(c答)
④より合同な図形で対応する辺の長さは等しいので AD=AE。
△ADEで二等辺三角形の底角は等しいので∠ADE=∠AED・・・⑤
弧ACに対する円周角なので∠ADE=∠ABC・・・⑤
正三角形ABCの内角なので∠ABC=60°・・・⑦
⑤⑥⑦より ∠ADE=∠AED=60°
△ADEの内角の和は180°なので
∠ADE=180°ー(∠ADE+∠AED)=180°ー(60°+60°)=60°・・・⑧
⑦⑧よりすべての内角が60°で等しいので△ADEは正三角形である。
(2)
与えられた条件(特に△ABCが正三角形)と(1)で求めた結論(△ADEが正三角形)を活用し、長さを求める。
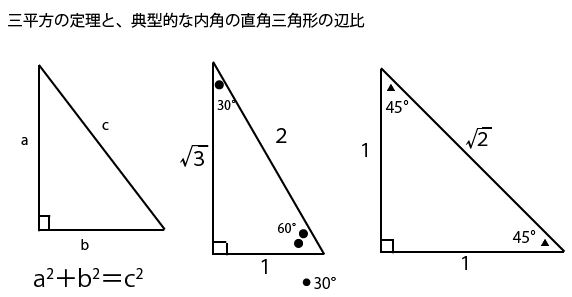
長さを求める時には三平方の定理や、典型的な内角の直角三角形の辺比を利用することが多いので確認しておこう。
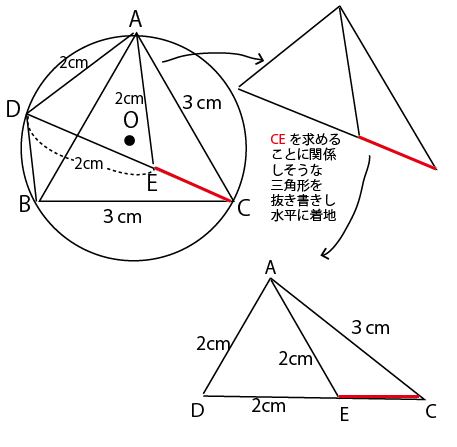
まず(2)の下の図(3番目の図)に△ABC、△ADEが正三角形であることを活用し、2cmと3cmの長さの部分を書きこんだ上で、CEを求めることに関係しそうな△ADCを抜き書きして水平において考える。
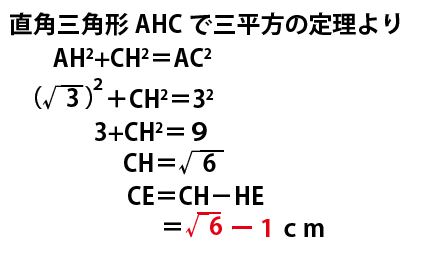
cm単位を省き、またAからDCに垂線をおろしその足をHとする。すると典型的な内角60°・30°の直角三角形の辺比から以下の数値がわかる。
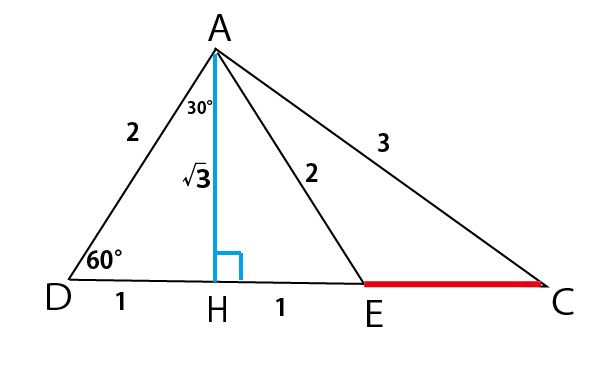
次に、直角三角形AHCで三平方の定理を使うとCHの長さがわかり、CEの長さも求められる。