【2017年前期・千葉県公立高校入試数学】第3問（二次関数）問題・解答・解説

【はじめに】私は、様々な理由で受験や進学で不利になっている子どもたち（原発被災避難世帯、児童養護施設、母子生活支援施設、ひとり親家庭など）の学習サポートを続けてまいりました。しかし直接伺える場所・教えられる子どもの数は限られますので、どなたでもご覧いただけるように、公式サイトにその内容をUPすることにいたしました。どうぞご活用ください。

【注意事項】
①前半に問題、後半に解答解説があります。問題にじっくりとりくみ考えたい人は、「以下解答解説です」の画像のところで画面を止める（印刷した場合はそれより下を見ない）ようにしてください。
②入試問題は実際は、白黒です。ただせっかくの画像上ですので、カラーをつけました。

【2017年前期・数学・第3問（二次関数）問題】

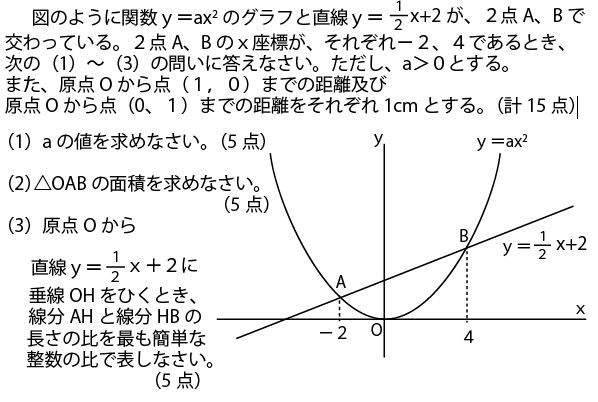
【解答】（1）a＝1／４　（2）6（cm2） （3)1:4

【解説】
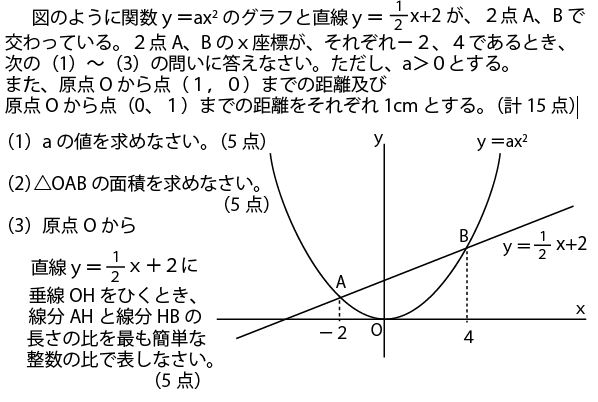
（1）aの値を求めよ。
点A、Bは直線と二次関数の交点なので、A・Bの座標を求め、そのどちらかがy=ax2上の点であることを活用してaを求める。

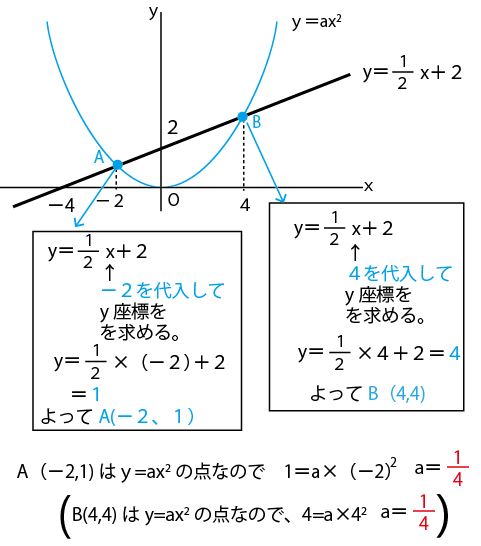
（2）△OABの面積を求めなさい。

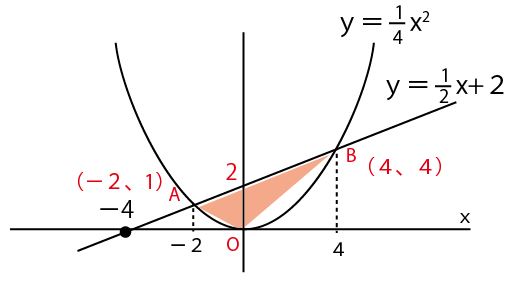
この面積を求める場合、形から考えてABを底辺とし、ABからOまでの高さを考えてみようとするかもしれない。

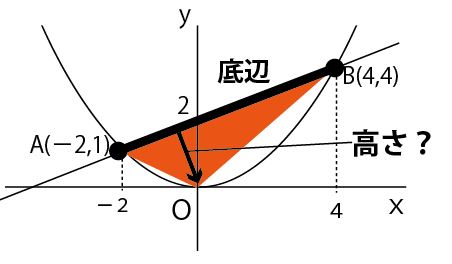
しかし、底辺の長さは三平方の定理で求められるかもしれないが、この斜めである高さ（矢印）を求めるのは困難である。

そこで発想を変えてみる。以下のようにｙ軸上に共通の底辺（赤線）を持つ２つの三角形（青・緑）の合計と考えてみよう。

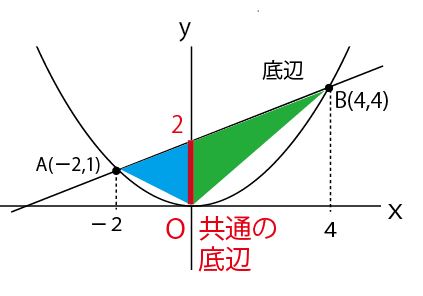
共通の底辺ODがｙ軸上なので、それと垂直である高さはｘ軸と並行となり、ｘ座標が０であるOD上との点との距離なので、A、Bのｘ座標の値の絶対値となる。

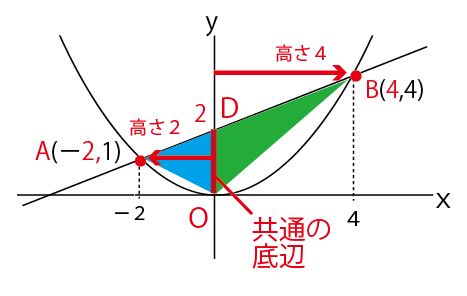
座標上の三角形を求める時は、この発想、つまりｘ軸上かｙ軸上に共通の底辺があり、高さは各頂点のｘ座標かｙ座標の絶対値である２つの三角形に分割して考え、それぞれの面積を合計する方法を使うことが

高校入試では多いので知っておいたほうがよい。

△OABの面積＝△OAD＋△ODB
＝１／２　×２×２　＋　１／２　×２×４＝２＋４＝６（cm2)（答）

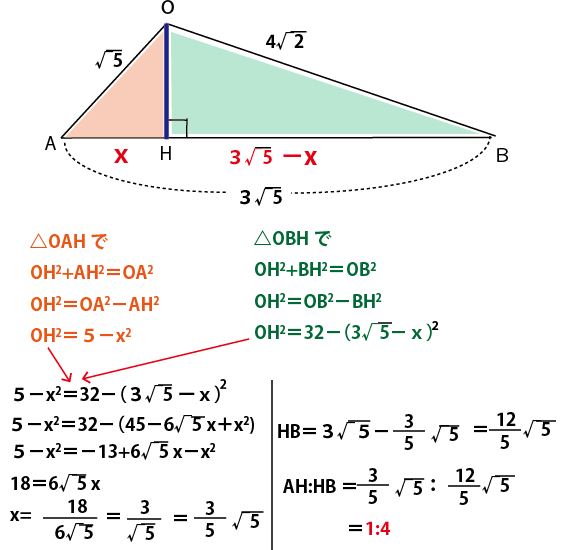
まずA・Bの座標（ｘ座標やｙ座標の差異）を利用しながら、図のオレンジの直角三角形で三平方の定理でABの長さを求める。

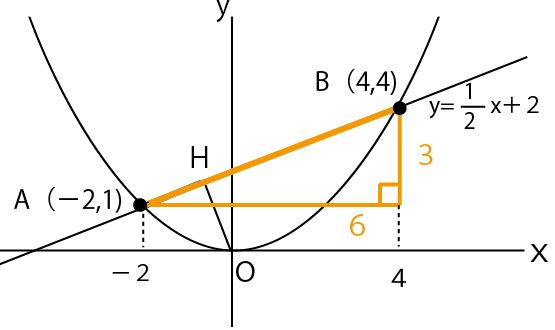
次に図の緑と青の直角三角形に注目し座標から三平方の定理でそれぞれの斜辺になるOA、OBの長さを求める。

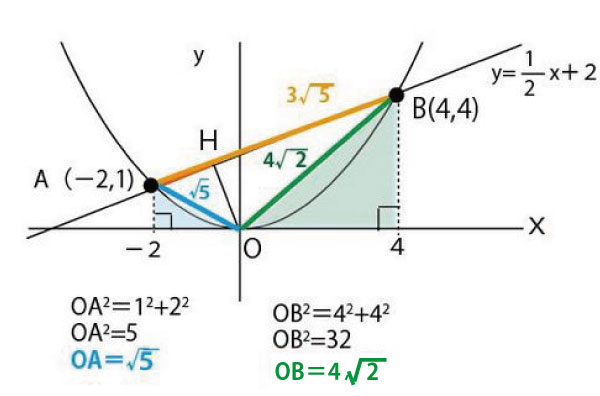
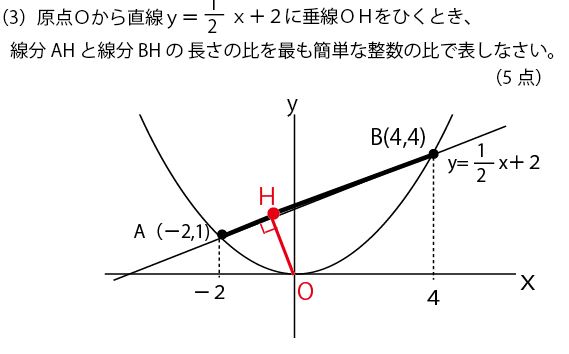
そして３辺の長さがわかった三角形OABを求めるべきAH：HBの比を求めやすいように、ABを底辺、OHが高さになる位置に描き直す。

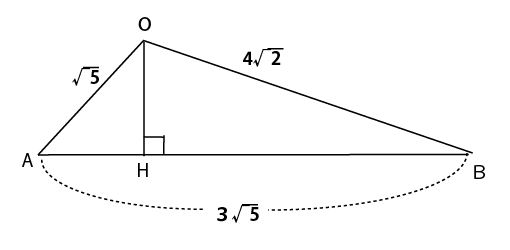
AHの長さをｘとすると、BHは３√５－ｘであり、図のオレンジと緑の直角三角形に注目し、三平方の定理を考える。このとき、この２つの三角形でOHが共通であることを活用し、ｘに関する式にまとめていくと
ｘ（AH）が計算でき、BH（３√５－ｘ）も計算でき、AH：BHの比を求められる。