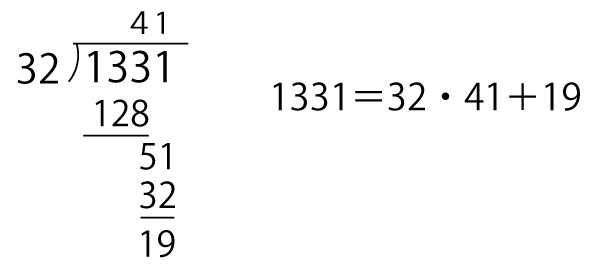2022年大学入試共通テスト「数ⅠA」第4問（整数論、不定方程式）（選択）問題（計20点）・解答・解説

【解説】

（1）

625²は5⁵で割り切れる（25²÷5⁵＝5⁸÷5⁵＝5³）。よって5⁵で割った時の余りは０である。
625²＝2⁸m²＋2⁵m＋１＝2⁵（2³ｍ²＋ｍ）＋１。よって2⁵で割った時の余りは１である。

（3）（2）の考察は、不定方程式
5⁵x－2⁵y＝１・・・
の整数解を調べるために利用できる。
x、ｙをの整数解とする。
5⁵xは5⁵の倍数、つまり5⁵で割った時の余りは０である。
また、は5⁵x=2⁵y＋１と変形でき、2⁵yは2⁵の倍数なので、
2⁵で割ったときの余りは１となる。
（2）より、625²も同様に、5⁵で割った時の余りは０、2⁵で割った時の余りは１である。
したがって5⁵xー625²も5⁵で割った時の余りは０、つまり5⁵で割り切れる。
また5⁵xー625²を2⁵で割った時の余りは、5⁵xを2⁵で割った時の余り１から、625⁵を2⁵で割った時の余り１を引いた値になるので、１ー１＝０、つまり,2⁵でも割り切れる。
よって、5⁵xー625²は5⁵でも2⁵でも割り切れ、5⁵と2⁵は互いに素なので、5⁵xー625²は5⁵・2⁵の倍数である。
5⁵xー625²＝5⁵・2⁵・Z（Zは整数）とすると
5⁵x＝625²＋5⁵・2⁵・Z
5⁵x＝5⁸＋5⁵・2⁵・Z
両辺を5⁵で割ると
ｘ＝5³＋2⁵・Z＝125＋32 Z
ｘが3桁の正の整数で最小となるのはZ＝0のときで、
x=125＋32×0＝125（サシス答、3点）
に代入すると
5⁵・125ー2⁵y＝１
3125×125ー32y＝１
390625ー32ｙ＝１
－32y=ー390624
ｙ＝12207（セソタチツ答、3点）

（4）
（1）（2）（3）を解いてきた流れの発想を使う。5⁴＝625で考えてきた流れを11⁴＝14641で置き換えて（1）（2）（3）の解法の流れに従えばよい。

は11⁵x=2⁵y＋１と変形でき、2⁵yは2⁵の倍数なので、
2⁵で割ったときの余りは１となる。
14641²も同様に、11⁵で割った時の余りは０、より2⁵で割った時の余りは１である。
したがって11⁵xー14641²も11⁵で割った時の余りは０、つまり11⁵で割り切れる。
また11⁵xー14641²を2⁵で割った時の余りは、11⁵xを2⁵で割った時の余り１から、14641⁵を2⁵で割った時の余り１を引いた値になるので、１ー１＝０、つまり,11⁵でも割り切れる。
よって、5⁵xー625²は11⁵でも2⁵でも割り切れる。11⁵と2⁵は互いに素なので、11⁵xー14641²は11⁵・2⁵の倍数である。
11⁵xー14641²＝11⁵・2⁵・Z₂（Z₂は整数）とすると
11⁵x＝14641²＋11⁵・2⁵・Z₂
11⁵x＝11⁸＋11⁵・2⁵・Z₂
両辺を11⁵で割ると
ｘ＝11³＋2⁵・Z²＝1331＋32 Z₂

1331を32で割ると

ｘが正の整数で最小となるのはZ₂＝－41のときでこのときｘ＝19（テト答、3点）
に代入して
19×161051ー32ｙ＝１
3059969−32y＝１
ー32y＝－3059968
y=95624（ナニヌネノ答、2点）