2017年大学入試センター数学IA（追試）第5問（図形）問題・解答・解説

私は、予備校で生物学を教えてきました。しかしながら、2011年の311（福島原発事故）で船橋や飯田橋に避難されてきた小中学生、その後、ひとり親家庭・児童養護施設・母子生活支援施設など様々な事情のある小中高校生の学習サポートを続ける中では、数学に対するニーズが大きく、数学を教えるようになりました。その関係で、今は、著作は数学、とくに子どもの時から大好きであった「図形」部分が3冊となっています。（アマゾン内での「朝倉幹晴」でご検索ください。）
　かつて教えた小中学生たちが今は大学入試センターの数学に挑戦する高校生となっています。しかし、直接、全員に教えるのは時間的にも困難です。そこで、誰でも見られるように、大学入試センター問題の解答・解説を発信することにしました。
　できれば、全ての設問の解答解説を作りたいと思っていますが、まずは一番得意分野である図形の問題を発信します。
　大学入試問題自体は白黒ですが、イメージの強化のためカラーを使いました。また、解き方は私独自のものも含んでいます。他の数学の授業や説明をお聴きになる機会がある方は、私の方法論や説明方法以外のアプローチの仕方もあると思いますので、気に入った方法をお使いください。

大学入試センター試験第5問は、図形の問題です。なかでもメネラウスの定理かチェバの定理が毎年きかれています。そしてこの2年間（2017・2018年）の問題には図は描かれておらず、受験生が余白に図を描き考えていく、その「描画しながら考えて行く」能力が問われています。描画しながら考え、考えたことをもとに描画の中の線の追加や線や長さの情報が小問ごとにわかってきた値を図に加筆して考えていくことが求められます。
　人生においても、行動しながら考え、考えたことをもとに次の行動を決めていくことが必要になってきます。そのことに似ているとも言えます。
　さてしたがって描画において、図をどのように、どの向きに描くかは受験生の側の自由です。大問の導入部分で与えられた線の長さや角度の情報をもとに、余白に描画して考えていきます。入試の約束で、定規の線の長さ表示や分度器は使えませんのであくまで「目分量」で描きます。ただ、あまりにも図が不正確だと後半の問題で、線の交点の位置が実際と異なり問題が解けなくなることがありますので、可能な限り正確に図を書くようにしましょう。
　描く向きは自由であり、問題集によって、同じ問題に対する描画の図の向きが異なることもあります。したがって、以下の私の描画はあくまで一つの例として考えてください。
当然ですが、またどんな向きに描画をしても、図の概形が間違っていなければ同じように正解がでますので安心ください。

 

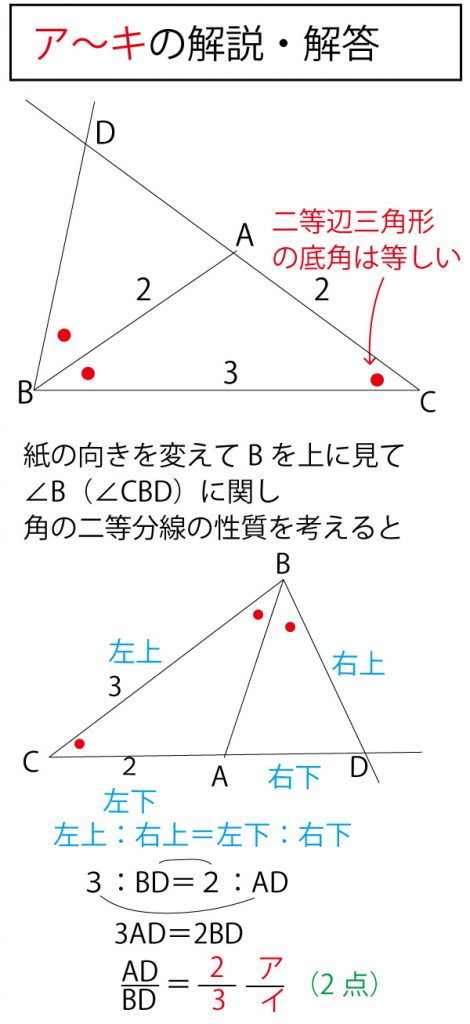
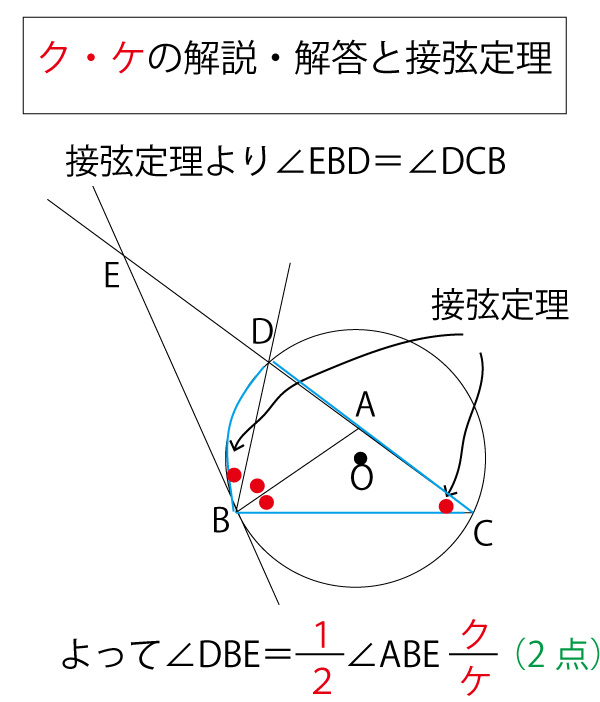
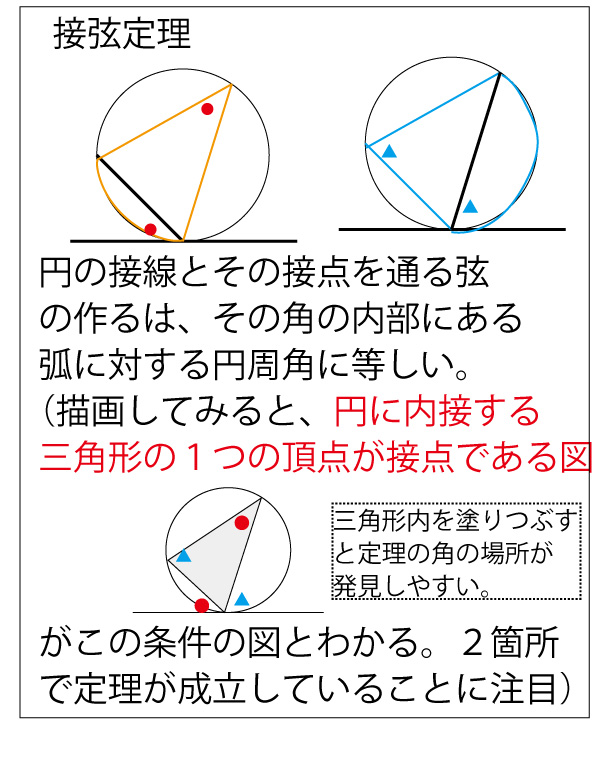
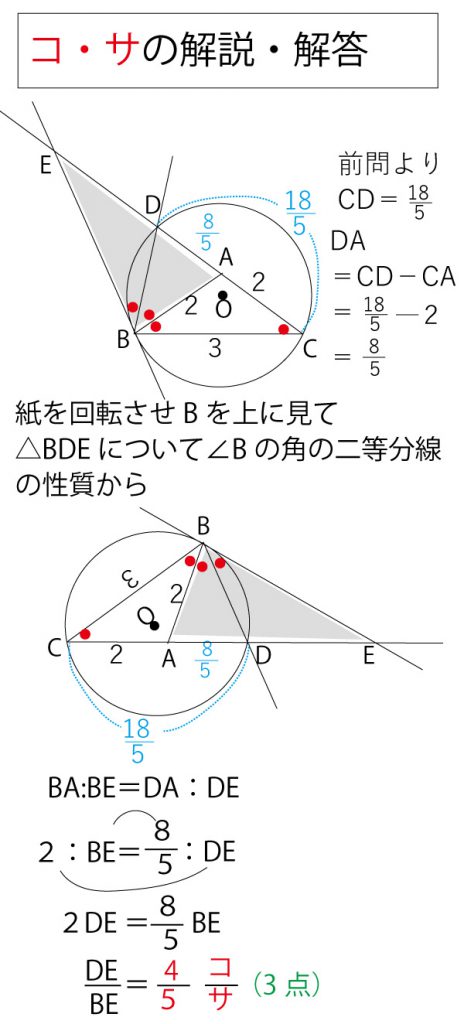
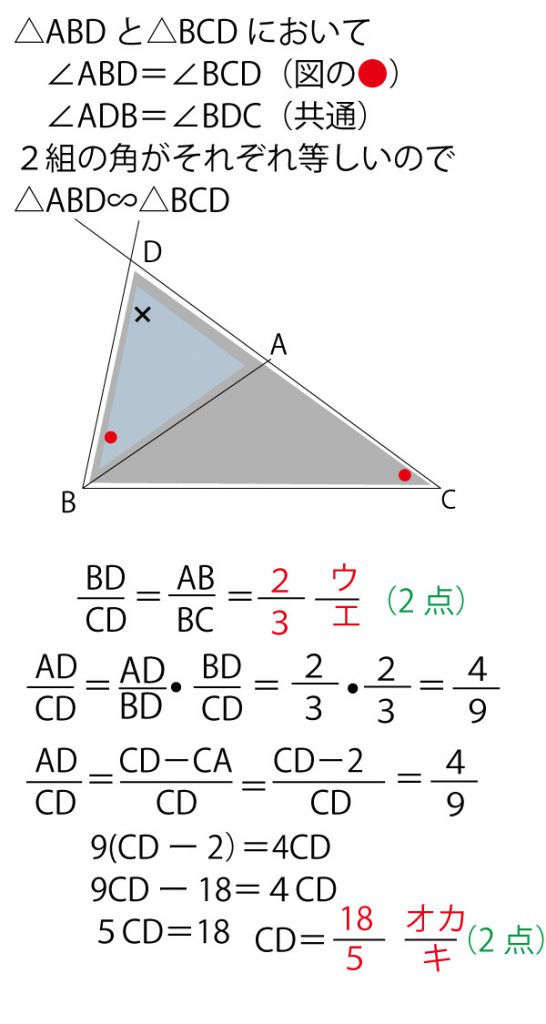
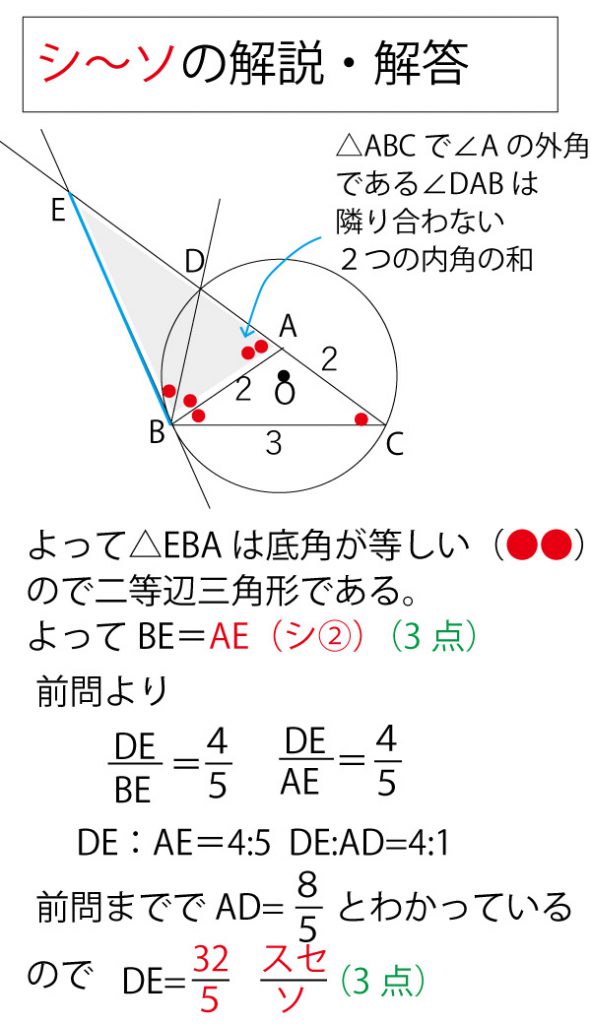
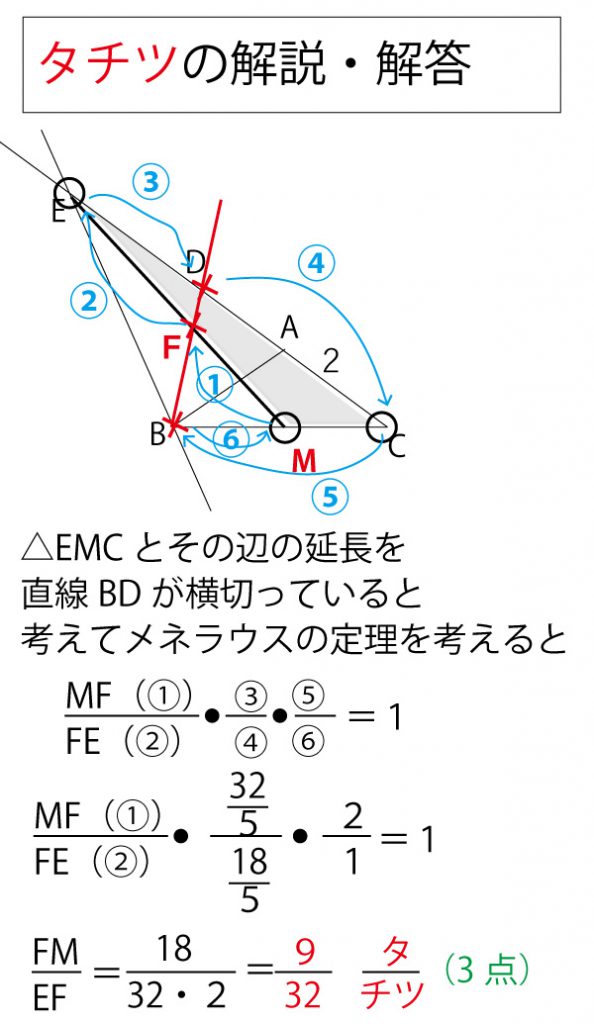
なお、メネラウスの定理の三角形（の辺の延長）と横ぎる直線と定理の関係の見出し方などは、2017年（本試）・2018年（本試）の解答・解説に補足説明してありますのでご覧ください。
https://a-sakura-mito.sakura.ne.jp/asakura2019/archives/5935

https://a-sakura-mito.sakura.ne.jp/asakura2019/archives/5839