2019年大学入試センター試験「数学ⅡB」第2問（微分・積分、配点30点）問題・解答・解説

2022年8月20日　予備校講師・船橋市議　朝倉幹晴

大学入試センター問題の問題・解答・解説を作成しました。学習や入試対策にご活用ください。

2019年大学入試センター試験「数学ⅡB」第2問（微分・積分）（計30点）問題

ｐ、qを実数とし、関数f（x）＝x³＋px²＋qxはｘ＝－１で極値２をとるとする。また、座標平面上の曲線ｙ＝f(x)をＣ、放物線y＝－kx²をＤ、放物線Ｄ上の点（a、－kx²)をＡとする。ただし、ｋ＞０、a＞０である。

（1）関数f(x)がx=－１で極値をとるので、ｆ´（－1）＝ア（1点）である。これとｆ（－1）＝２より、ｐ＝イ（1点）、q＝ウエ（1点）である。よって、ｆ（ｘ）は、ｘ＝オ（2点）で極小値カキ（1点）をとる。

（2）点Aにおける放物線Dの接戦をℓとする。Dとℓおよびｘ軸で囲まれた図形の面積Ｓをaとkを用いて表そう。

（3）さらに、点Aが曲線C上にあり、かつ（2）の接線ℓがCにも接するとする。このときの（2）のSの値を求めよう。

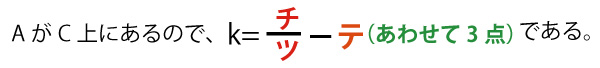
ℓとCの接点のｘ座標をｂとすると、ℓの方程式はｂを用いて
ｙ＝ト（b²－ナ）ｘーニｂ³・・・・・
（ㇳナ2点、ニ1点）
と表される。の右辺をｇ（ｘ）とおくと
f(x)－g(x)＝（ｘ－ヌ）²(x＋ネｂ）（ヌ1点、ネ2点）

と因数分解されるので、a=－ネｂとなる。

[next_p]