2021年大学入試共通テスト「数学IA」第5問（選択・図形・配点20点）問題・解答・解説

2021年2月8日 2021年2月13日

asakura

2021年２月8日　予備校講師、「円」「三角形」「図形の証明」著者、船橋市議　朝倉幹晴

2021年1月17日（日）に実施された大学入試共通テスト数学IA第5問（ア～タ）（計20点、選択）の問題・解答・解説です。

　2021年受験生は２次試験に向けた復習に、2022年以降の受験生は来年の準備にご活用ください。
実際の入試問題は白黒印刷ですが、画面上ですのでカラーを一部使いました。ア～タには当てはまる数字か選択肢の番号を入れる形で答えてください。

第5問（選択・配点20点）

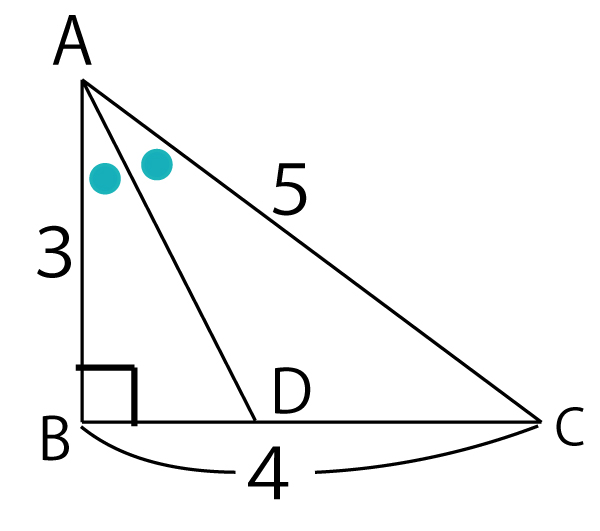
△ABCにおいて、AB＝３、BC＝４、AC＝５とする。∠BACの二等分線と辺BCとの交点をDとすると

BD＝（2点）　　AD＝　（2点）　

である。

　また、∠BACの二等分線と△ABCの外接円Oとの交点で点Aとは異なる点をEとする。△AECに着目すると

AE＝（2点）　
である。

　△ABCの２辺ABとACの両方に接し、外接円Oに内接する円の中心をPとする。円Pの半径をrとする。さらに、円Pと外接円Oとの接点をFとし、直線PFと外接円Oとの交点で点Fとは異なる点をGとする。このとき

AP＝（2点）、PG＝ケ－ｒ（2点）

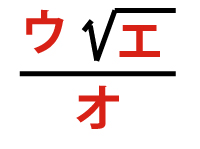
と表せる。したがって、方べきの定理によりｒ＝　　（2点）である。
　△ABCの内心をQとする。内接円Qの半径はシ（2点）で、AQ＝（2点）
である。また、円Pと辺ABとの接点をHとすると、AH＝である。
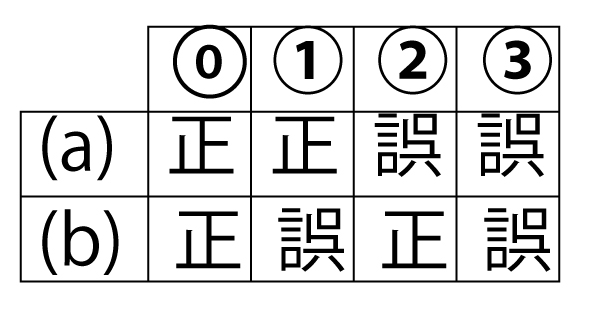
以上から、点Hに関する次の（a)、（b)の正誤の組合せとして正しいものはタ（2点）である。