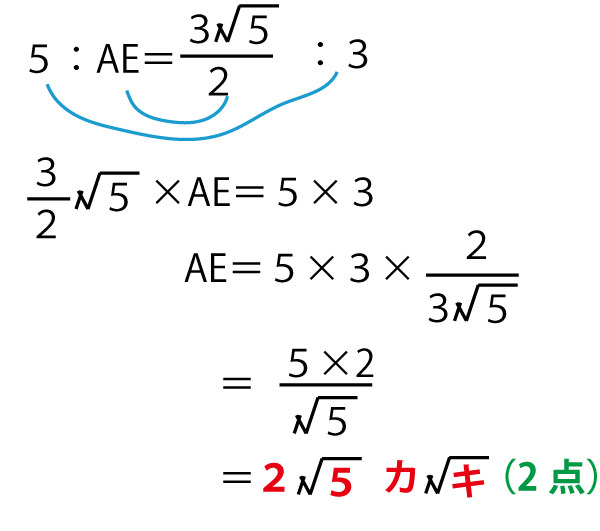2021年大学入試共通テスト「数学IA」第5問（選択・図形・配点20点）問題・解答・解説

2021年2月8日 2021年2月13日

asakura

解説

ア～オについて

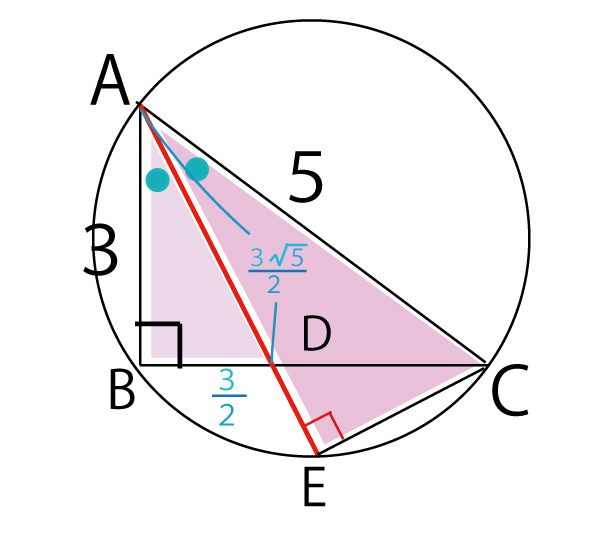
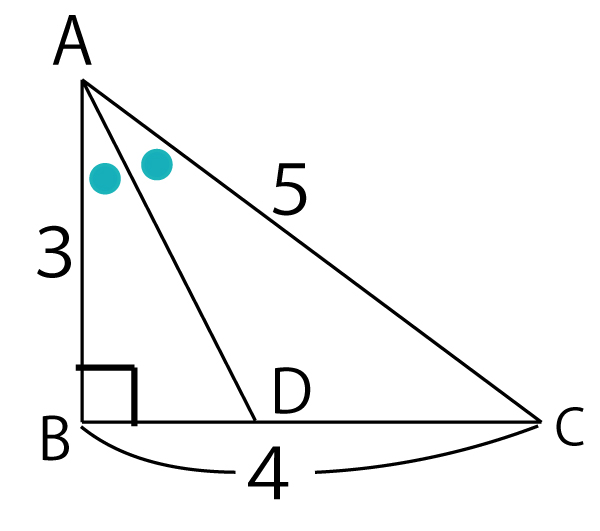
辺比３：４：５の三角形は、3²＋4²＝５²（９＋16＝25）が成り立つ典型的な直角三角形である。

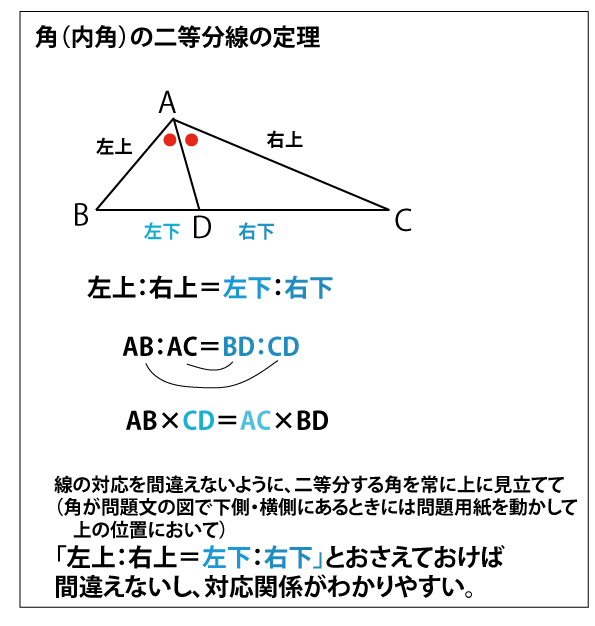
角の二等分線の定理より
AB（左上）：AC（右上）＝BD（左下）：CD（右下）
AB：AC＝BD：BCーBD
BD：BCーBD＝AB：AC
BD：４ーBD＝３：５
５BD＝３（４－BD）
５BD＝12－３BD
８BD＝12
BD＝12／８

カ・キについて

「タレスの定理」から直角三角形ABCの斜辺ACは外接円の直径である。したがって△AECにおいて、∠AECは直径ACを弦とする半円の弧に対する円周角なので、∠AEC＝90°。よって△AECも直角三角形である。

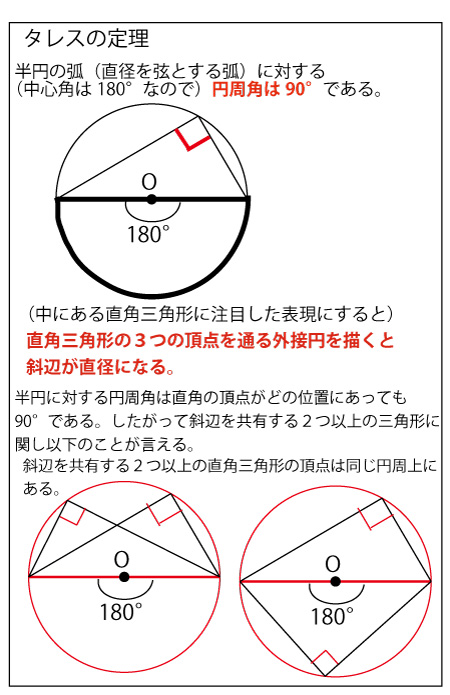
△AECと△ABDにおいて
∠AEC＝∠ABD＝90°・・・
AD（AE）は∠BACの二等分線なので
∠EAC＝∠BAD・・・

より、2組の角がそれぞれ等しいので
△AEC∽△ABD

相似である三角形どうしで対応する辺の比は等しいので
AC：AE＝AD：AB

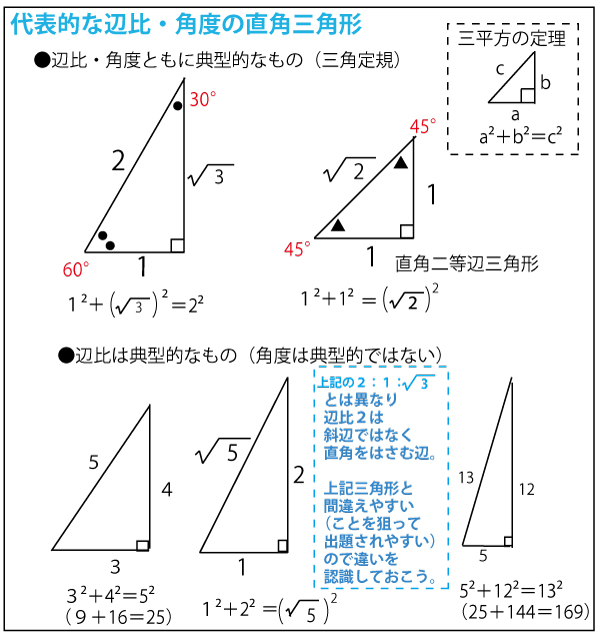
ちなみに、この辺比１：２：　（１と２が直角をはさむ辺、が斜辺）
の直角三角形は入試で出題される典型な直角三角形である。そのことを見抜くことができると計算の目安ともなる。以下で入試で出題されやすい代表的な直角三角形の辺比と角度を確認しておこう。

ク・ケについて

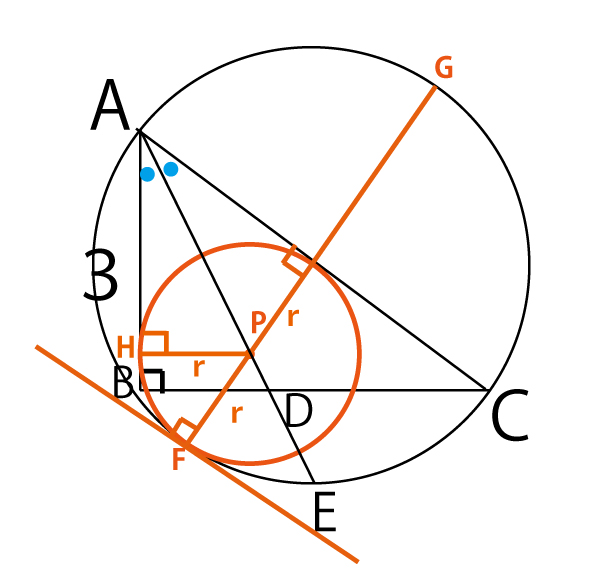
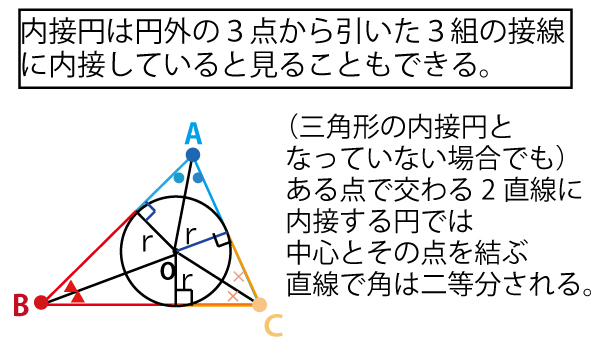
「△ABCの２辺ABとACの両方に接し、外接円Oに内接する円の中心をPとする。円Pの半径をrとする。さらに、円Pと外接円Oとの接点をFとし、直線PFと外接円Oとの交点で点Fとは異なる点をGとする。」を図示してみよう。また説明のため、（本文中の後半にあるように）ABと円Pとの接点をHとし、Fで２つの円に接する接線を描く。

円PはABとACに内接するので、その中心Pと円外の点Aを結ぶ線分APは、∠BACを二等分する。つまりAPは∠BACの二等分線であるADと重なりPはAD上にある。また円の接線と円中心と接点を結ぶ半径は直交するので∠PHA＝90°。したがって△APH∽△ADB
よって相似比より、

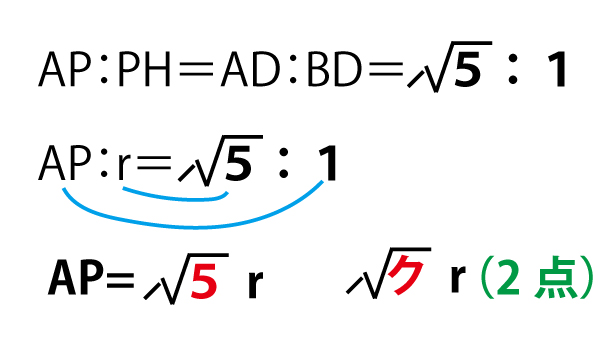
Fでの接線を描いてみると、接点Fと2円それぞれの中心を結ぶ半径は直交する。したがってFGは外接円の中心も通るのでFGは外接円の直径とわかる。前問で、BCも外接円の直径であり、AC＝５なのでFG＝AC＝５。
よってPG＝FGーPF＝５ーｒ（　ケーｒ（2点））

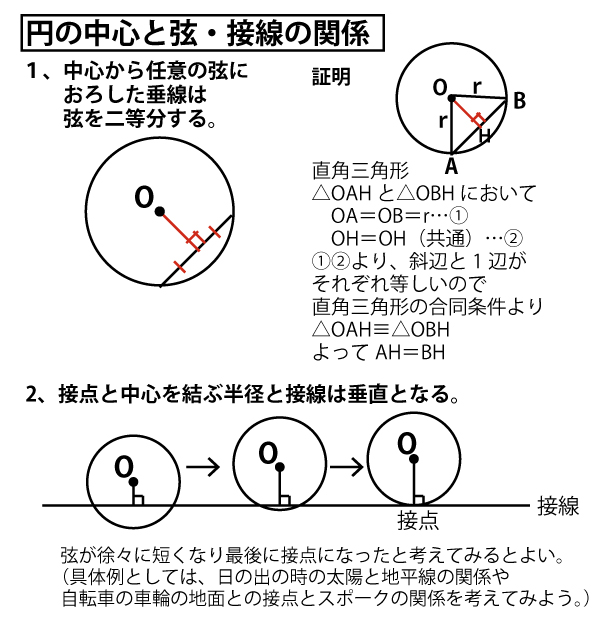
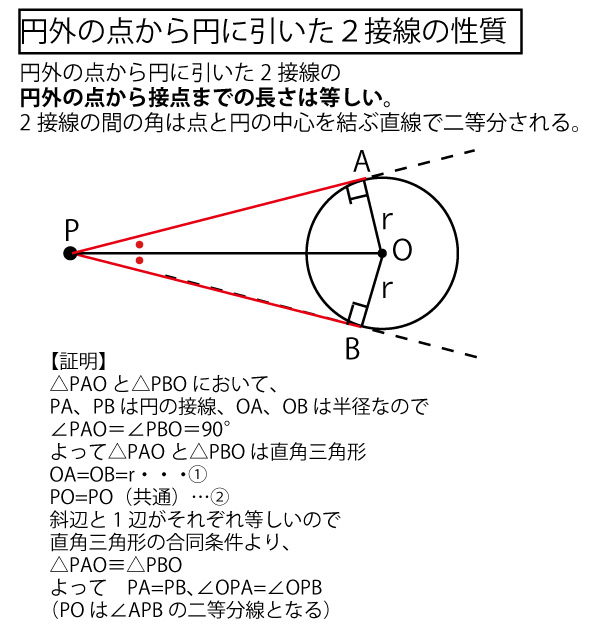
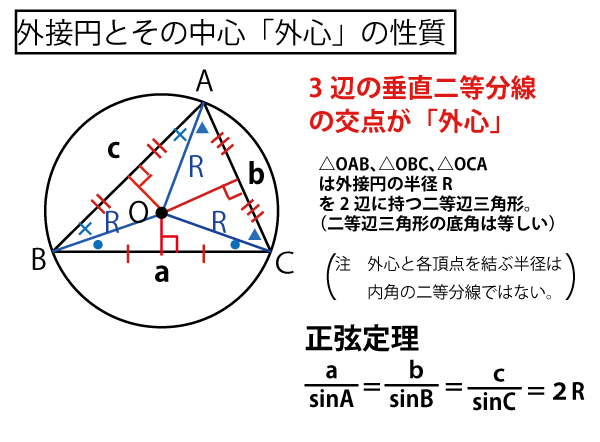
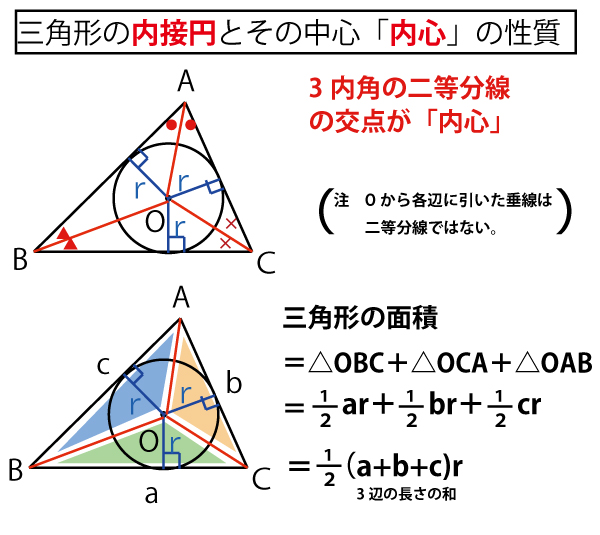
★円と弦・接線の関係、外接円と内接円の知識のまとめ

なお、内接円と外接円の説明の（　）書きの部分は、内接円・外接円に関して、知識が交差し、混乱し間違えやすい部分である。
・外心と各頂点を結ぶ線分（半径）は、それぞれの内角の二等分線ではない。
・内心から各辺におろした垂線は、各辺を二等分しない。
（混乱・間違いを防ぐために強調したが、二等辺三角形や正三角形など特殊な三角形の場合においては、二等分線になったり、二等分することもありうる。）

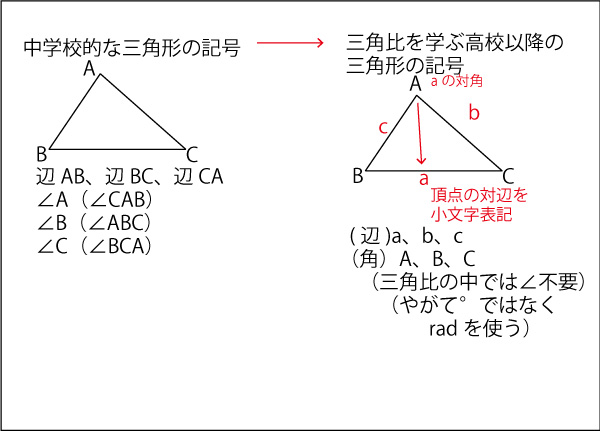
高校で使う辺a、b、cや角Ａ，Ｂ、Ｃの表記方法については以下を確認しておこう。

この見方がしっかりしていれば本問題は容易に解くことができる。

コ・サについて

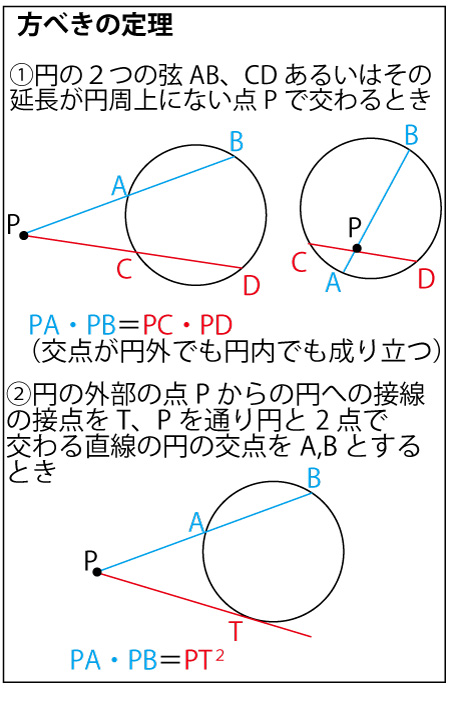
直線ACとFB（赤線）の交点Pという視点で外接円で「方べきの定理」を考える。

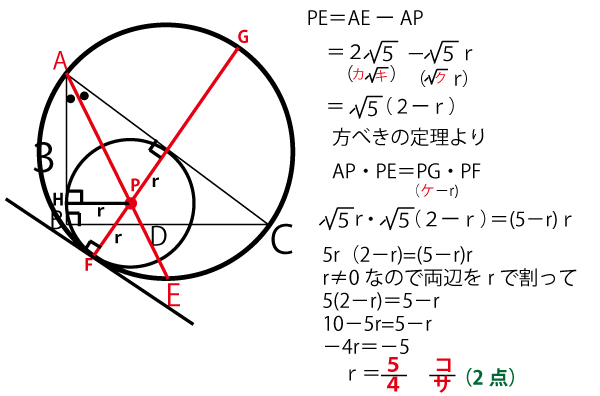
シ～ソについて

シ～ソに関係する部分を赤で強調した図を下に描いてみる。この時、QからABに下ろした垂線のABの交点をIとすると、QIが内接円の半径となる。そして、内接円の性質や三角形の相似比を使って計算する。（実際の入試の時は黒の鉛筆しか使えないので、前に描いた図に太線で加筆したり、図が重なって見えにくいと感じたら描き直す）

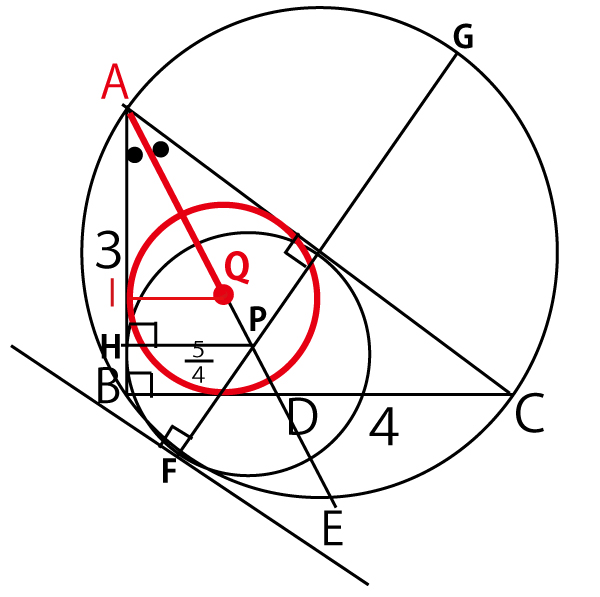
△ABCは直角三角形で面積は１／２×BC×AB＝１／２×４×３＝６
三角形の面積＝１／２×　３辺の長さの和　×内接円の半径（QI）なので
６＝１／２×（３＋４＋５）×QI
６＝１／２　×12×QI
６＝６×QI
QI（内接円Qの半径）＝１（シ　2点）

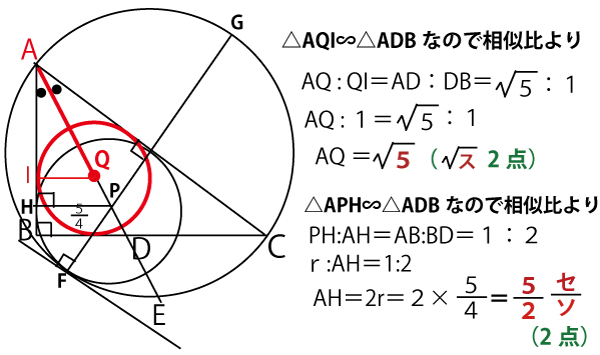
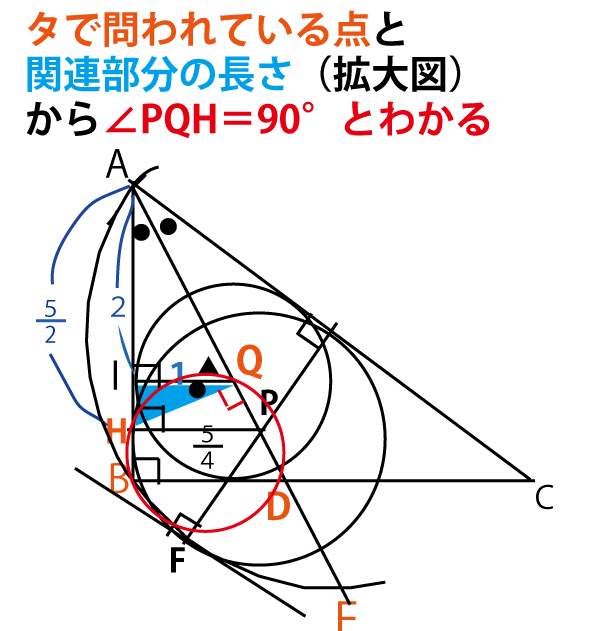
タについて

（a)点Hは3点B、D、Qを通る円の周上にある。
（b）点Hは3点B、E、Ｑを通る円の周上にある。
の正誤を求める問題なので、「四角形BDQHと四角形BEDHに外接円が描けるか」の問題と読み返してみる。
それでは、まず三角形と四角形の外接円に関して整理してみよう。

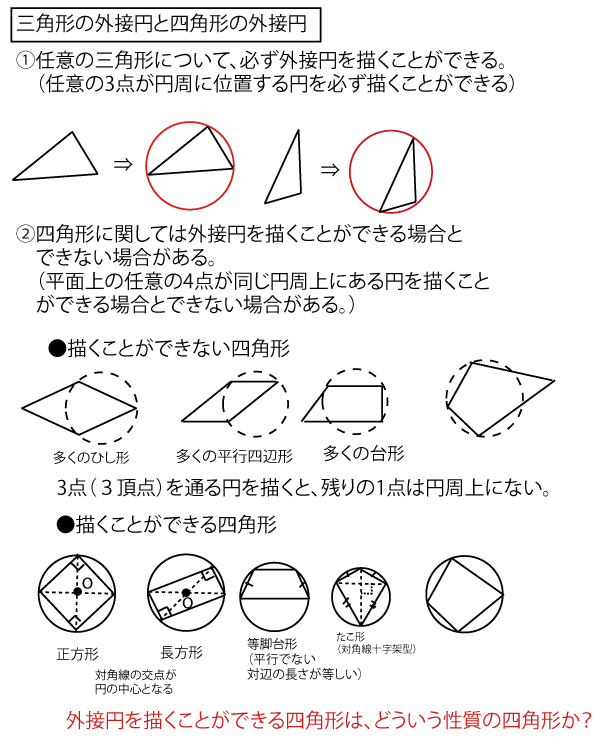
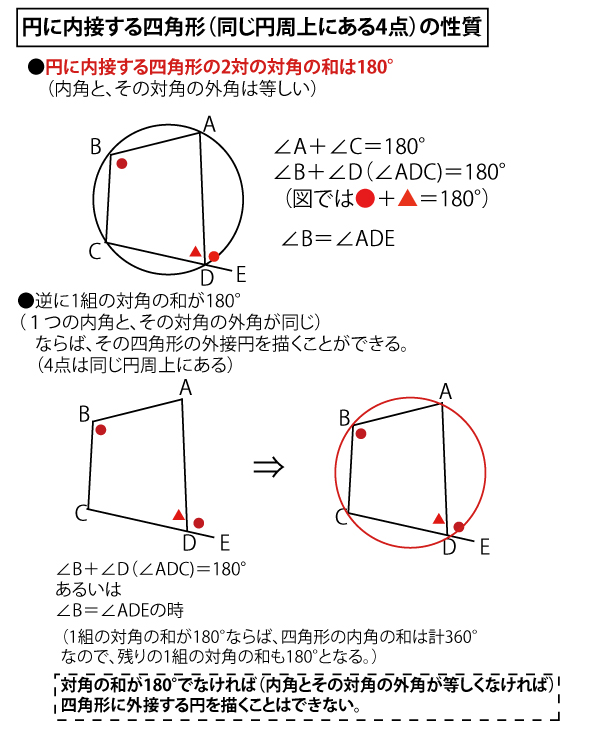
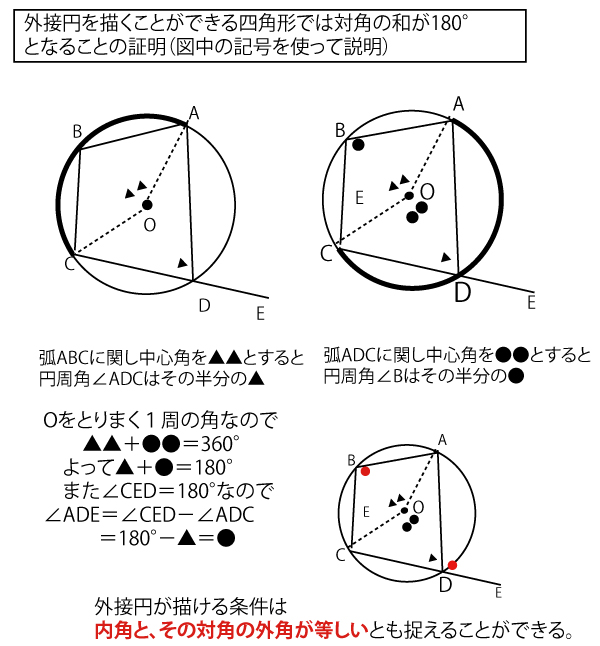
それでは、本設問タで注目する4点を結ぶ四角形BDQH、四角形BEQHに関して対角の和が180°とわかれば、外接する円が描ける（4点は同じ円周上にある）し、逆に180°でなければ描けない（4点は同じ円周上にはない）ことがわかる。
以下のように、注目する4点と、関連部分のこれまで求めてきた長さに注目しよう。

図中の青い直角三角形△QHIに注目する。
△AQI∽△ADBであり、AI：IQ＝AI：１＝２：１。よってAI＝２
IH＝AHーAI＝５／２　ー２＝１／２
IQ：IH＝１：１／２＝２：１なので、
△QHI∽△AQI
よって∠QAI＝∠HQI（図の●）
△QAIで直角以外の2鋭角の和は90°なので
∠QAI（●）＋∠AQI（図で▲）＝90°
よって∠AQH＝∠AQI（●）＋∠HQI（▲）＝90°
よって∠HQD＝90°
∠HBD＋∠HQD=90°＋90°＝180°
（四角形BDQHの1組の対角の和が180°なので）
あるいは
∠HBD＝∠AQH=90°
（１つの内角とその対角の外角が等しいので）
四角形BDQHは外接円が描ける。4点B、D、Q、Hは同じ円周上にある。
図から、あきらかにＨ、Ｂ、Ｑを通る円周上にはＦはない（Ｆは円周の外にある）。
よって（a)は正で、(b)は誤。（タ、2点）

本設問は、「円」と「三角形」（あるいは四角形の外接円）に関しての中学・高校の図形の知識を総動員することが求められる問題である。拙著「円」「三角形」は、文字通り「円」と「三角形」にこだわって小中高の知識を一貫させて記述した本である。値段も「円」は314円（＋税）、「三角形」は333円（＋税）と図形にちなんで設定した。アマゾンで注文可能である。ぜひ、お読みいただき、「円」「三角形」を徹底的に会得してほしい。